本试题 “几种液体的密度见附表1实验室里现有的甲、乙、丙、丁四种量筒的规格见附表2如果要求一次尽可能精确地量出100g的煤油来,应选用( )附表1 几种液体的密度 物...” 主要考查您对体积的测量,量筒的使用
密度公式的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 体积的测量,量筒的使用
- 密度公式的应用
体积:
体积表示物体所占空间的大小,用字母V,来表示。
体积的单位也采用国际制单位,有立方米(m3)、立方分米(dm3)、立方厘米(cm3)。换算关系为:1m3= 1000dm3:1dm3=1000cm3;1m3=106cm3。
容积:
容积是指容器内部窄间的大小,容积单位有升 (L)、毫升(mL)。
换算关系为:1L=1000mL。与体积单位的对应关系是1L=1dm3;1mL=1cm3。
量筒:
1. 量筒的使用:
①量筒的规格量筒是用来量取液体体积的一种玻璃仪器,一般规格以所能度量的最大容量(mL)表示,常用的有10mL,20mL,25mL,50mL,100mL,250mL、500mL,1000mL等多种规格。
②量筒的选择方法:
量筒外壁刻度都是以mL为单位。10mL量筒每小格表示0.1mL,而50mL量筒有每小格表示1mL或0.5mL的两种规格。可见,绝大多数的量筒每小格是量筒容量的1/100,少数为1/50。
量筒越大,管径越粗,其精确度越小,由视线的偏差所造成的读数误差也就越大。
所以,实验中应根据所取溶液的体积,尽量选用能一次量取的最小规格的量筒。分次量取会引起较大误差。如量取70mL液体,应选用100mL量筒一次量取,而不能用10mL量筒量取7次。
③液体的注入方法
向量筒里注入液体时,应用左手拿住量筒,使量筒略倾斜,右手拿试剂瓶,标签对准手心。使瓶口紧挨着量筒口,让液体缓缓流入,待注入的量比所需要的量稍少(约差1mL)时,应把量筒水平正放在桌面上,并改用胶头滴管逐滴加入到所需要的量。
④量筒的刻度
量筒没有“0”刻度,“0”刻度即为其底部。一般起始刻度为总容积的1/10或1/20。例如:10mL量筒一般从0.5mL处才开始有刻度线,所以,我们使用任何规格的量筒都不能量取小于其标称体积数的1/20以下体积的液体,否则,误差太大。应该改用更小的合适量筒量取。
在实验室做化学实验时,量筒的刻度面不能背对着自己,这样使用起来很不方便。因为视线要透过两层玻璃和液体,不容易看清。若液体是浑浊的,就更看不清刻度,而且看刻度数字也不顺眼,所以刻度面正对着自己为好。
⑤读取液体的体积方法
注入液体后,要等一会,使附着在内壁上的液体流下来,再读取刻度值。否则,读出的数值将偏小。
读数时,应把量筒放在平整的桌面上,观察刻度时,视线、刻度线与量筒内液体的凹液面最低处三者保持水平,再读出所取液体的体积数。否则,读数会偏高或偏低。
⑥关于量筒仰视与俯视的问题
在看量筒的容积时是看液面的中心点
仰视时视线斜向上视线与筒壁的交点在液面下所以读到的数据偏低,实际值偏高。
俯视时视线斜向下视线与筒壁的交点在液面上所以读到的数据偏高,实际值偏低。

2. 注意事项
①量筒面上的刻度是指室内温度在20℃时的体积数。温度升高,量筒发生热膨胀,容积会增大。由此可知,量筒是不能加热的,也不能用于量取过热的液体,更不能在量筒中进行化学反应或配制溶液。
②量筒一般只能用于要求不是很严格时使用,通常可以应用于定性分析和粗略的定量分析实验,精确的定量分析是不能使用量筒进行的,因为量筒的误差较大,此时可用移液管或滴定管来代替。
③从量筒中倒出液体后是否要用水冲洗要看具体情况而定。如果是为了使所取的液体量更准确,似乎要用水洗涤后并把洗涤液倒入所盛液体的容器中,这是不必要的。因为在制造量筒时已经考虑到有残留液体这一点;相反,如果洗涤反而使所取体积偏大。如果是用同一量筒再量别的液体,这就必须用水冲洗干净并干燥,为防止相互污染。
④10mL的量筒一般不需读取估读值。因为量筒是粗量器,并且又是量出仪器,在倒出所量取的液体时,总会有1~2滴(1滴相当于0.05mL)附着在内壁上而无法倒出,其相差的体积大小已经和其最小刻度差相同,所以估读值再准确也无多大意义,只需读取到0.1mL。
规格大于10mL的量筒一般需要读取估读值,若不读取,误差反而更大。因此,无论多大规格的量筒,一般读数都应保留到0.1mL
3. 量筒的使用要做到“五会”
①会选。任何一只量筒都有一定的测量范围,即量程,要能根据被测量的量选择量程合适的量筒。
②会放。使用量筒测量时,量筒要平稳地放置于水平桌面上。
③会看。读取量筒的数据时,若液面是凹液面,视线应以凹液面底部为准;若液面是凸液面,视线应以凸液面顶部为准。
④会读。要会根据量筒刻度的分度值读出准确值,同时要读出分度值的下一位,即估计值。
⑤会用。
测体积的方法:
①用量筒直接测液体体积;
②规则形状的物体可用刻度尺测出相关长度,算出体积;
③用代替法可测不规则形状容器的容积。先将容器灌满水,然后将水倒入量筒中即可测其容积;
④用量筒、水、细线可测密度比水大的固体体积。具体步骤是:在量筒中加入适量的水,记下水的体积V0;用细线系住物体并轻轻放入量筒中,记下此时水和物体的体积为V1;物体的体积V=V1-V0。用量筒测固体的体积,采取的是“排液法”,依据的是等量替代;
⑤形状不规则、且漂浮在液体上的固体的体积的测量,可用非常规的办法测量。由于物体漂浮于液面,可以用“针压法”,也就是用一枚细针将漂浮物压入液体中;或用一密度比液体密度大得多且不溶于液体的物体将漂浮物拉入水中,此法称为“助沉法”。如用量筒、水、细针(或细线、铁块)可测密度比水小的固体的体积。
体积表示物体所占空间的大小,用字母V,来表示。
体积的单位也采用国际制单位,有立方米(m3)、立方分米(dm3)、立方厘米(cm3)。换算关系为:1m3= 1000dm3:1dm3=1000cm3;1m3=106cm3。
容积:
容积是指容器内部窄间的大小,容积单位有升 (L)、毫升(mL)。
换算关系为:1L=1000mL。与体积单位的对应关系是1L=1dm3;1mL=1cm3。
量筒:
1. 量筒的使用:
①量筒的规格量筒是用来量取液体体积的一种玻璃仪器,一般规格以所能度量的最大容量(mL)表示,常用的有10mL,20mL,25mL,50mL,100mL,250mL、500mL,1000mL等多种规格。
②量筒的选择方法:
量筒外壁刻度都是以mL为单位。10mL量筒每小格表示0.1mL,而50mL量筒有每小格表示1mL或0.5mL的两种规格。可见,绝大多数的量筒每小格是量筒容量的1/100,少数为1/50。
量筒越大,管径越粗,其精确度越小,由视线的偏差所造成的读数误差也就越大。
所以,实验中应根据所取溶液的体积,尽量选用能一次量取的最小规格的量筒。分次量取会引起较大误差。如量取70mL液体,应选用100mL量筒一次量取,而不能用10mL量筒量取7次。
③液体的注入方法
向量筒里注入液体时,应用左手拿住量筒,使量筒略倾斜,右手拿试剂瓶,标签对准手心。使瓶口紧挨着量筒口,让液体缓缓流入,待注入的量比所需要的量稍少(约差1mL)时,应把量筒水平正放在桌面上,并改用胶头滴管逐滴加入到所需要的量。
④量筒的刻度
量筒没有“0”刻度,“0”刻度即为其底部。一般起始刻度为总容积的1/10或1/20。例如:10mL量筒一般从0.5mL处才开始有刻度线,所以,我们使用任何规格的量筒都不能量取小于其标称体积数的1/20以下体积的液体,否则,误差太大。应该改用更小的合适量筒量取。
在实验室做化学实验时,量筒的刻度面不能背对着自己,这样使用起来很不方便。因为视线要透过两层玻璃和液体,不容易看清。若液体是浑浊的,就更看不清刻度,而且看刻度数字也不顺眼,所以刻度面正对着自己为好。
⑤读取液体的体积方法
注入液体后,要等一会,使附着在内壁上的液体流下来,再读取刻度值。否则,读出的数值将偏小。
读数时,应把量筒放在平整的桌面上,观察刻度时,视线、刻度线与量筒内液体的凹液面最低处三者保持水平,再读出所取液体的体积数。否则,读数会偏高或偏低。
⑥关于量筒仰视与俯视的问题
在看量筒的容积时是看液面的中心点
仰视时视线斜向上视线与筒壁的交点在液面下所以读到的数据偏低,实际值偏高。
俯视时视线斜向下视线与筒壁的交点在液面上所以读到的数据偏高,实际值偏低。

2. 注意事项
①量筒面上的刻度是指室内温度在20℃时的体积数。温度升高,量筒发生热膨胀,容积会增大。由此可知,量筒是不能加热的,也不能用于量取过热的液体,更不能在量筒中进行化学反应或配制溶液。
②量筒一般只能用于要求不是很严格时使用,通常可以应用于定性分析和粗略的定量分析实验,精确的定量分析是不能使用量筒进行的,因为量筒的误差较大,此时可用移液管或滴定管来代替。
③从量筒中倒出液体后是否要用水冲洗要看具体情况而定。如果是为了使所取的液体量更准确,似乎要用水洗涤后并把洗涤液倒入所盛液体的容器中,这是不必要的。因为在制造量筒时已经考虑到有残留液体这一点;相反,如果洗涤反而使所取体积偏大。如果是用同一量筒再量别的液体,这就必须用水冲洗干净并干燥,为防止相互污染。
④10mL的量筒一般不需读取估读值。因为量筒是粗量器,并且又是量出仪器,在倒出所量取的液体时,总会有1~2滴(1滴相当于0.05mL)附着在内壁上而无法倒出,其相差的体积大小已经和其最小刻度差相同,所以估读值再准确也无多大意义,只需读取到0.1mL。
规格大于10mL的量筒一般需要读取估读值,若不读取,误差反而更大。因此,无论多大规格的量筒,一般读数都应保留到0.1mL
3. 量筒的使用要做到“五会”
①会选。任何一只量筒都有一定的测量范围,即量程,要能根据被测量的量选择量程合适的量筒。
②会放。使用量筒测量时,量筒要平稳地放置于水平桌面上。
③会看。读取量筒的数据时,若液面是凹液面,视线应以凹液面底部为准;若液面是凸液面,视线应以凸液面顶部为准。
④会读。要会根据量筒刻度的分度值读出准确值,同时要读出分度值的下一位,即估计值。
⑤会用。
测体积的方法:
①用量筒直接测液体体积;
②规则形状的物体可用刻度尺测出相关长度,算出体积;
③用代替法可测不规则形状容器的容积。先将容器灌满水,然后将水倒入量筒中即可测其容积;
④用量筒、水、细线可测密度比水大的固体体积。具体步骤是:在量筒中加入适量的水,记下水的体积V0;用细线系住物体并轻轻放入量筒中,记下此时水和物体的体积为V1;物体的体积V=V1-V0。用量筒测固体的体积,采取的是“排液法”,依据的是等量替代;
⑤形状不规则、且漂浮在液体上的固体的体积的测量,可用非常规的办法测量。由于物体漂浮于液面,可以用“针压法”,也就是用一枚细针将漂浮物压入液体中;或用一密度比液体密度大得多且不溶于液体的物体将漂浮物拉入水中,此法称为“助沉法”。如用量筒、水、细针(或细线、铁块)可测密度比水小的固体的体积。
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比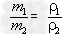 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比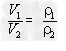 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
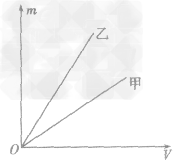
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
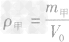 ,ρ乙=
,ρ乙= 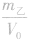 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。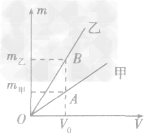
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,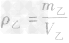
(2)写出该物理量比的表达式:
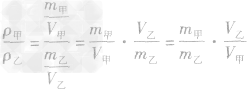
(3)化简:代入已知比值的求解:
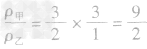
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
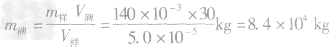 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
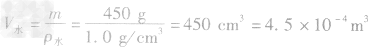 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为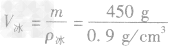 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,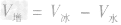 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
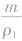 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=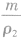 ,合金的体积
,合金的体积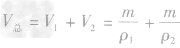 ,则合金的密度
,则合金的密度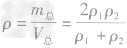
在(2)中两种金属的体积相等,设为
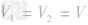 ,合金的体积
,合金的体积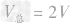 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=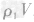 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为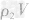 ,合金的质量m总
,合金的质量m总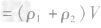 ,合金的密度为
,合金的密度为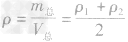 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
发现相似题
与“几种液体的密度见附表1实验室里现有的甲、乙、丙、丁四种量筒...”考查相似的试题有:
- 完成下列单位换算以及添加单位:(1)0.2t= _____kg(2)4.5g=______kg(3)32mL=____cm3=______L=______m3(4)7.8×103kg/m3...
- 巧测一个瓶子的容积,用刻度尺测出瓶底的直径,然后给瓶子装一些水如图所示,测出水面到瓶底的高度h1,再堵住瓶口,将瓶子倒...
- 下面是小方和小王设计的“测食用油密度”的实验方案,请完善他们的方案,并回答后面的问题:(1)小方的方案:用调节平衡的天平...
- 美术课上同学们用橡皮泥捏动物模型时,想知道橡皮泥的密度有多大.课后,他们取了同一块橡皮泥,采用了两种实验方案,来测量...
- 如图所示,装有水的圆柱形薄壁容器的底面积为400cm2。体积为2000cm3。将密度为4×103kg/m3的矿石放在漂浮在水面上的A木块上静...
- 某同学用天平和量筒测物体密度,在用量筒测物体体积时,没有将物体全部浸入量筒的水中,而其他步骤都是正确的,则此同学最终...
- 有一容积为5L的食用油桶里装了满满一桶食用油,若该食用油的密度为0.9×103kg/m3,那么这桶食用油的质量是______kg,要是炒菜...
- 某实心铜雕的质量为445kg,现要用蜡将其复制成大小一样的蜡制品,求需用多少千克的蜡?[ρ铜=8.9×103kg/m3,ρ蜡=0.9×103kg/m3].
- 分别装有相同的质量的水、盐水、酒精的三个相同容器中液面高低如图.已知ρ盐水>ρ水>ρ酒精,则甲液体是______,乙液体是____...
- 一间普通教室里空气的质量最接近( )A.200吨B.200千克C.2000克D.20千克