本试题 “(1)小丽总结初中物理实验探究方法后发现:当要研究的物理量不易直接测量时,都需要想办法把它们的大小间接地测量出来;当要探究的物理量与多个因素有关时,...” 主要考查您对动能的影响因素
密度公式的应用
固体密度的测量
摩擦力的大小
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 动能的影响因素
- 密度公式的应用
- 固体密度的测量
- 摩擦力的大小
物体的质量和物体的运动速度。
动能影响因素的实验探究:
探究:探究动能的大小与哪些因素关有?
猜想:影响动能的因素:质量、速度、物体的大小形状、接触面的粗糙程度、接触面大小
实验设计:选择质量、速度、大小形状设计实验进行验证;
1.大小形状、速度相同,质量不同
将质量不同小车从斜面同一高度释放(如图)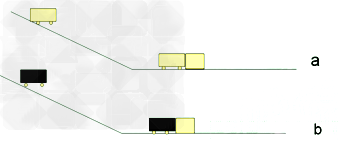
2.大小形状、质量相同,速度不同。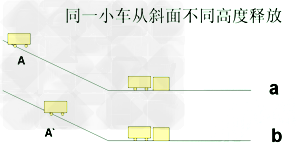
3.质量、速度相同,大小形状不同。 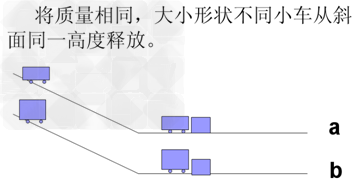
4.实验结论:
a.速度、大小形状相同,质量越大动能越大。
b.大小形状、质量相同,速度越大动能越大。
c.质量、速度相同,大小形状不同动能相同。
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比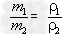 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比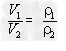 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
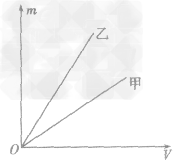
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
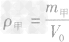 ,ρ乙=
,ρ乙= 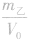 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。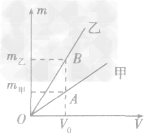
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,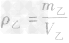
(2)写出该物理量比的表达式:
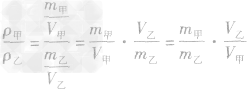
(3)化简:代入已知比值的求解:
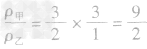
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
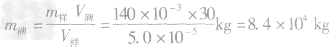 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
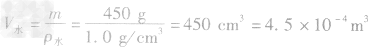 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为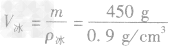 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,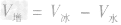 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
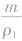 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=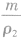 ,合金的体积
,合金的体积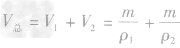 ,则合金的密度
,则合金的密度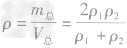
在(2)中两种金属的体积相等,设为
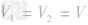 ,合金的体积
,合金的体积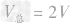 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=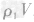 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为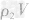 ,合金的质量m总
,合金的质量m总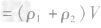 ,合金的密度为
,合金的密度为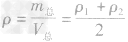 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
原理:由密度公式
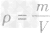 可知,要测量某种物质的密度,需要测量由这种物质构成的物体的质量的体积。
可知,要测量某种物质的密度,需要测量由这种物质构成的物体的质量的体积。测量方法:
1. 形状规则的固体:质量可用天平测量,体积可直接用刻度尺测长、宽、高等,并利用体积公式算出,如正方体的体积V=a3,圆柱体的体积V=πr2h,长方体的体积V=abc,根据
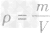 求得密度。
求得密度。2. 形状不规则的固体(不溶于水):
(1)体积可用“排水法”间接测出
(2)质量可用天平测量
①先在量筒中倒入适量水,读出水的体积V1(水的多少以刚好淹没固体为宜。水过多,放入固体后液面会超过量程;水过少,不能淹没固体)
②将固体用细线拴住慢慢放人量筒内水中,并使其全部淹没,此时读出水与固体的总体积V2
③由V=V2-V1,得出固体体积。
最后根据
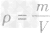 求得密度。
求得密度。Ⅰ方法一:天平量筒法
例:有一块形状不规则的石块,欲测量它的密度,所需哪些器材并写出实验步骤,并表示出测量的结果。
分析:用天平和量筒测定密度大于水的物质的密度,可用排水法测体积。
实验原理: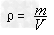
实验器材:天平(砝码)、量筒、烧杯、滴管、线、水、石块
实验步骤:
(1)用调节好的天平,测出石块的质量m;
(2)在量筒中倒入适量的水,测出水的体积V1;
(3)将石块用细线拴好,放在盛有水的量筒中,(排水法)测出总体积V2;
实验结论:ρ=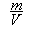 =
=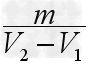 。
。
Ⅱ方法二:助沉法
例:有一块形状不规则的蜡块,欲测量它的密度,所需哪些器材并写出实验步骤,并表示出测量的结果。
分析:用天平和量筒测定密度小于水的物质的密度,可用助沉法测体积。
实验原理: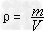
实验器材:天平(砝码)、量筒、烧杯、滴管、线、水、蜡块、铁块。
实验步骤:
(1)用调节好的天平,测出蜡块的质量m;
(2)在量筒中倒入适量的水,如图甲将蜡块和铁块用细线拴好,先将测铁块没入水中,测出水和石块的体积V1
(3)再将蜡块浸没在水中,如图乙。(助沉法)测出水、石块、蜡块的体积总体积V2;
实验结论: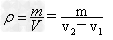
注意:物质的密度比水小,放在量筒的水中漂浮,不能直接用量筒测出体积。例题中采用的方法是助沉法中的沉锤法,还可以用针压法,即用一根很细的针,将物体压入量筒的水中,忽略细针在水中占据的体积,则可用排水法直接测出物体的体积了。
Ⅲ方法三:等浮力法
例:小明家买的某品牌的牛奶喝着感觉比较稀,因此他想试着用学过的知识测量一个这种牛奶的密度。他先上网查询了牛奶的密度应该为1.03g/cm3,然后他找来一根粗细均匀的细木棒,在木棒的表面均匀地涂上一层蜡,并在木棒的一端绕上一段金属丝(体积不计),做成了一枝“密度计”,小明又找来一个足够深的盛水容器和一把刻度尺,请你帮助小明利用这些器材设计一个测量牛奶密度的方案。要求写出主要的测量步骤并推导出计算牛奶密度的公式(有足量的水和牛奶)。
实验原理:漂浮条件、阿基米德原理。
实验器材:刻度尺、粗细均匀的细木棒、一段金属丝、烧杯、水、牛奶。
实验步骤:
(1)将一段金属丝绕在木棒的一端,制成“密度计”,用刻度尺测出其长度L;
(2)将“密度计”放入盛有水的烧杯中,使其漂浮在水中,用刻度尺测出“密度计”露出水面的高度h水;
(3)将“密度计”放入盛有牛奶的烧杯中,使其漂浮在牛奶中,用刻度尺测出“密度计”露出牛奶液面的高度h牛。
实验结论:因为“密度计”在水中和在牛奶中,均处于漂浮状态。因此“密度计”在水中和在牛奶中受到的浮力都等于“密度计”的重力。“密度计”的重力不变,所以两次浮力相等。即F牛=F水,根据阿基米德原理可得:
ρ牛gV牛排=ρ水gV水排
ρ牛gSh牛排=ρ水gSh水排
∵h牛排=L-h牛h水排=L-h水
∴ρ牛(L-h牛)=ρ水(L-h水)
牛奶的密度: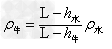
注意:从给定的器材看,即无量筒,也无天平,此时解题的着眼点就不能局限于利用质量、体积测密度。应该展开丰富的联想,而给出“密度计”,是和浮力有关的,就要联想到利用浮力测液体的密度。这种利用两次浮力相等来测密度,我们简称为“等浮力法”。
Ⅳ弹簧测力计法(也可称双提法)
例:张小清同学捡到一块不知名的金属块,将它放到水中可以沉没,现在,小清同学想测出它的密度,但身边只有一支弹簧秤、一个烧杯及足量的水,请你帮她想一想,替她设计一个测量金属块密度的实验过程,写出实验步骤
分析与解:
这是一道典型的利用浮力知识测密度的试题。阿基米德原理的重要应用就是已知浮力求体积。它的基本思路就是用弹簧测力计测出浮力,利用水的密度已知,求得物体的体积,即可计算出物体的密度值。
实验原理:阿基米德原理
实验器材:一支弹簧秤、一个烧杯及足量的水、金属块、线。
实验步骤:
(1)用细线系住金属块,在烧杯中倒入适量的水;
(2)用弹簧测力计测出金属块受到的重力G;
(3)用弹簧测力计测出金属块浸没在水中受到的拉力F。
实验结论:
注意:利用弹簧测力计提着金属块测一次重力;再提着金属块测一次金属块在水中时弹簧测力计的拉力。因此简称为双提法。这一实验使用的仪器少,操作简单,是常用的测量物体密度的方法。
两个互相接触的物体,当它们做相对运动时,在接触面上会产生一种阻碍相对运动的力,这种力就叫做摩擦力。
产生的条件:
(1)两物体接触面粗糙不平;
(2)两物体之间发生相对运动或具有相对运动趋势;
(3)两物体之问相互挤压发生弹性形变,接触面上有压力产生。
摩擦力的作用效果:总是阻碍物体之间的相对运动或相对运动趋势。
摩擦力的方向:
摩擦力方向总是沿接触面的切线方向,和物体的相对运动方向或相对运动趋势的方向相反。
说明:“相对运动方向”不是“运动方向”。我们以人走路时地面与鞋底间的摩擦力为例来说明这个问题。人走路时,脚用力向后蹬地,脚相对地向后运动,摩擦力阻碍了脚向后运动,但有利于脚向前运动,因此地面给鞋底的摩擦力方向是与人的运动方向相同的。由此说明,摩擦力有时阻碍运动,有时有利于运动,但无论哪种情况,必与相对运动方向相反。
控制变量法研究影响滑动摩擦力大小的因素:
在探究“摩擦力的大小与什么因素有关”这个问题时用到控制变量法。为了探究摩擦力大小与压力大小和接触面的粗糙程度是否有关,先使木块在同一木板上面滑动,即保持了接触面的粗糙程度这一个量相同,改变压力的大小,看滑动摩擦力是否改变;然后保持压力这一个物理量相同,改变接触面的粗糙程度,让木块分别在较光滑的小板上和较粗糙的毛巾面上滑动,测出摩擦力的大小,根据测出的数据进行判断得出滑动摩擦力的大小与压力大小和接触面的粗糙程度有关的结论。
例1:小明在探究“影响摩擦力大小的因素”实验中,记录的结果如下表所示:
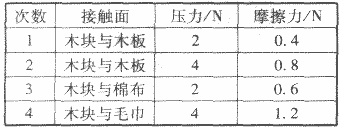
(1)在这个实验中,使用的是控制变量法,第1、3 两次实验中的变量是________,控制的变量是______。得出的结论是:在压力相同时,接触面越粗糙,摩擦力越大。
(2)在探究压力对摩擦力的影响时,可采用_______ 两次的实验结果,得出的结论是:_______________________________________________
解析:从表格中的数据可以看出,第1、3两次实验中的压力相等,产生的摩擦力不同,说明在压力相同时,接触面越粗糙(木块与棉布),摩擦力越大。根据控制变量的思想,若研究摩擦力与压力大小的关系,应保持接触面不变,即第l、2两次实验,从数据中看出,压力越大,摩擦力越大。
答案:(1)接触面的粗糙程度压力的大小
(2)1、2在接触面的粗糙程度不变时,压力越大,摩擦力越大
平衡状态中摩擦力大小的判断:
根据二力平衡的知识,一对平衡力一定大小相等,方向相反,作用在同一物体上,故可对物体进行受力分析,从而来判断摩擦力情况。这也是判断各种摩擦力情况最行之有效的方法。例:体重为490N的某同学用双手握住竖直的木杆匀速上攀,他所受的摩擦力( )
A.等于490N,方向竖直向下
B.等于490N,方向竖直向上
C.大于490N,方向竖直向下
D.小于490N,方向竖直向上
解析:人匀速上攀,受力平衡,重力等于摩擦力,且方向相反。
答案:B
滑动摩擦力:
定义: 当一个物体在另一个物体表面上滑动时,会受到另一个物体阻碍它滑动的力叫滑动摩擦力。
大小:F=μ×FN。FN:正压力(不一定等于施力物体的重力)μ:动摩擦因数
方向:滑动摩擦力的方向总是沿接触面,并且与物体相对运动方向相反。
静摩擦力:
定义:若两相互接触且相互挤压,而又相对静止的物体,在外力作用下如只具有相对滑动趋势,而又未发生相对滑动,则它们接触面之间出现的阻碍发生相对滑动的力,谓之“静摩擦力”。
大小:静摩擦力根据外力而变化,但有一个最大值,叫做最大静摩擦力。最大静摩擦力略大于滑动摩擦力。
方向:跟接触面相切,跟相对运动趋势方向相反。
与“(1)小丽总结初中物理实验探究方法后发现:当要研究的物理量...”考查相似的试题有:
- 如图所示,在探究“物体的动能与哪些因素有关”的实验中,将A、B、C三个小球先后从同一装置的hA、hB、hC高度处滚下(mA=mB<mC...
- 小明同学在探究物体的质量与体积的关系时,得到如下数据,由此可知物体的质量与体积的关系是 。
- 植树节里,小倩同学用水桶提了15L水给刚栽上的树浇水,桶中水深为30cm.(g取10N/kg)求:(1)15L水的质量是多少?(2)水对...
- 一个空瓶装满水时,瓶与水的总质量是64g,装满煤油时,瓶与油的总质量是56g,则瓶的容积是______cm3,瓶的质量是______g.(ρ...
- 一个瓶子最多能装0.5kg的水,最多能装_________m3的酒精.(ρ酒精=0.8×103kg/m3);将体积分别为V1、V2的水和酒精混合,发现...
- 质量、外形和体积完全相同的铁球、木球、铅球和铝球(ρ木<ρ铝<ρ铁<ρ铅),其中只有一个球是实心的,则空心部分最小的球是...
- 将一木块按4:1的比例分成大小两木块,则大木块与小木块的密度之比是______;甲乙两实心物体的质量比是2:1,密度比是1:2,...
- 冬季大雪造成很多房屋垮塌.屋顶的雪到底有多重?竟然能把屋顶压塌,小明同学找来器材进行测量.他的实验步骤如下:①用天平测...
- 用量筒装某种液体,测得的体积为V,液体与量筒的总质量为m.改变液体的体积,重复上述实验,得到了一系列V与m对应值,在m-V图...
- 如图所示的量筒是以 为单位标度的,最小分度值是 ;测量时如果如图那样读数,则读出的液体体积与真实值相比 (填“偏大”、“偏...