本试题 “建设中的洋浦跨海大桥全长3.3km ,汽车行驶速度按 80km/h 设计,则该桥建成后(1)假设允许行人上桥,请你估算:如果你按正常速度走完该桥需要多长时间。(2...” 主要考查您对速度公式及其应用
惯性的危害和利用
重力的计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 速度公式及其应用
- 惯性的危害和利用
- 重力的计算
速度的公式:
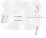 ,其中v表示速度,s表示路程,t表示时间。
,其中v表示速度,s表示路程,t表示时间。
注意:
①应用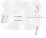 计算时,单位要统一。s用米(m),t用秒(s)作单位时,速度v的单位为米/秒 (m/s);当s用千米(km),t用小时(h)时,速度v的单位为千米/时(km/h)。
计算时,单位要统一。s用米(m),t用秒(s)作单位时,速度v的单位为米/秒 (m/s);当s用千米(km),t用小时(h)时,速度v的单位为千米/时(km/h)。
②公式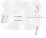 的三个物理量必须对应于同一物体。
的三个物理量必须对应于同一物体。
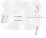 ,其中v表示速度,s表示路程,t表示时间。
,其中v表示速度,s表示路程,t表示时间。注意:
①应用
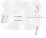 计算时,单位要统一。s用米(m),t用秒(s)作单位时,速度v的单位为米/秒 (m/s);当s用千米(km),t用小时(h)时,速度v的单位为千米/时(km/h)。
计算时,单位要统一。s用米(m),t用秒(s)作单位时,速度v的单位为米/秒 (m/s);当s用千米(km),t用小时(h)时,速度v的单位为千米/时(km/h)。②公式
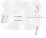 的三个物理量必须对应于同一物体。
的三个物理量必须对应于同一物体。火车过桥(隧道)问题:
火车穿过隧道时,火车头进人隧道就开始算起,直到火车尾离开隧道才叫做火车通过了隧道,所以火车穿过隧道经过的路程应该等于隧道长与车身长度的和。过大桥时也类似,火车通过大桥经过的路程等于桥长加车长。故对于本身有长度的物体过桥问题小结如下:物体通过的路程等于桥长与物体本身长度的和。
例1:一列火车长200米,用20s的时间穿过了一条100m长的隧道,该火车如果以这样的速度通过长 3.4km的大桥,要用多长时间?
解析:火车穿过隧道时所走的路程: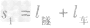 =100m+200m=300m,时间t1=20s,火车的速度:vl =
=100m+200m=300m,时间t1=20s,火车的速度:vl =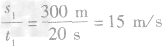 ,此速度也是火车通过大桥的速度,火车通过大桥的路程:
,此速度也是火车通过大桥的速度,火车通过大桥的路程: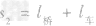 =3400m+ 200m=3600m,通过此桥需要的时间为
=3400m+ 200m=3600m,通过此桥需要的时间为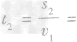
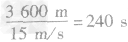 。
。
答案:240s
出租车问题:
1.出租车的速度表示车辆行驶过程中的行进速度,指针指示的数值就是该时刻的速度值,采用的单位为km/h。
2.里程示数窗表示该车行驶的总路程,某段时间的路程就等于这段时间内两个示数的差。
3.出租车票据上给出的上车、下车时间间隔为车行驶时间,里程就是这段时间内出租车通过的路程。利用这些信息,可以解决与出租车有关的多种问题。
例某人乘出租车时得到一张天津市客运出租行业专用发票,如表所示,此人乘车时间为____;该车这段时间内运动的平均速度为____km/h。
解析:根据出租车票据的起止时问,可以知道此人乘车时间为10min,出租车行驶的路程是5.5km,利用速度公式求出汽车的平均速度为: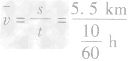 =33km/h。
=33km/h。
惯性是一把双刃剑,既有利又有弊。
惯性的利用
生活中利用惯性的例子很多,如:用手向地上洒水时,手撩起水向前运动,当手停止运动后,由于惯性,手带起的水仍要继续向前运动,所以就被洒出去;在跳远比赛时,运动员跳起后,由于惯性,在空中仍保持一定的速度继续向前运动.最后落在前方;汽车快到达终点时,熄火后由于惯性仍能前进一段距离,这样可以节省汽油;人骑车也是一样,当自行车运动起来后,人停止蹬车,自行车仍会向前运动一段距离,并不会立即停下等,这样的例子还有很多这些都是惯性在生活中的广泛应用。如果没有惯性,这些现象将不复存在。因此对于有益的惯性.我们往往想办法来增大它。由于惯性只与质量有关,质量越大,惯性越大。因此在汽油机、柴油机等热机上我们通过增加飞轮的质量来增加它的惯性,以保持飞轮能持续地旋转下去。
惯性的危害
惯性对我们的影响不都是有益的,在生活中的很多方面,惯性对我们造成了不利的影响,尤其是在交通方面。比如汽车在突然启动、突然刹车、突然转弯或速度大小突然改变时,站在车厢里的乘客的脚虽然与汽车一起改变运动状态,但是人的上身由于惯性还会保持原来的运动状态,冈此往往会摔倒,严重时会造成人身伤害;特别是高速行驶的汽车,由于惯性,在刹车后很难立即停下,还要向前运动一段距离,这样往往会导致车祸的发生。为了避免悲剧的发牛,人们采用了很多应对方法。如为了防止汽车在突然刹车或突然减速时对人造成伤害,强制司乘人员使用安全带,并存汽车上安装安全气囊;另外还对汽车的行驶速度做出了限制。我国的交通法规明确规定:机动车行驶时在没有道路中心线的城市道路速度不能超过30km/h,公路上不能超过40km/h;在同方向只有l条机动车道的城市道路不能超过50km/h,公路上不能超过70km/h。需要说明的是,这些方法虽然都能减小惯性带来的危害,但是却并不能从根本上减小惯性。要真正地减小惯性就要减小物体的质量,针对当前我国运输业超载现象非常普遍的情况,有关部门做出规定:公路客运车辆载客超过额定乘员,货运车辆超过核定承载重量的,会处以相应的经济处罚,严重的还会扣留机动车。这是因为对载重汽车进行限载,既可以减小它对地面的压强,又能减小它的惯性,从而降低车祸的发生率。
惯性的利用
生活中利用惯性的例子很多,如:用手向地上洒水时,手撩起水向前运动,当手停止运动后,由于惯性,手带起的水仍要继续向前运动,所以就被洒出去;在跳远比赛时,运动员跳起后,由于惯性,在空中仍保持一定的速度继续向前运动.最后落在前方;汽车快到达终点时,熄火后由于惯性仍能前进一段距离,这样可以节省汽油;人骑车也是一样,当自行车运动起来后,人停止蹬车,自行车仍会向前运动一段距离,并不会立即停下等,这样的例子还有很多这些都是惯性在生活中的广泛应用。如果没有惯性,这些现象将不复存在。因此对于有益的惯性.我们往往想办法来增大它。由于惯性只与质量有关,质量越大,惯性越大。因此在汽油机、柴油机等热机上我们通过增加飞轮的质量来增加它的惯性,以保持飞轮能持续地旋转下去。
惯性的危害
惯性对我们的影响不都是有益的,在生活中的很多方面,惯性对我们造成了不利的影响,尤其是在交通方面。比如汽车在突然启动、突然刹车、突然转弯或速度大小突然改变时,站在车厢里的乘客的脚虽然与汽车一起改变运动状态,但是人的上身由于惯性还会保持原来的运动状态,冈此往往会摔倒,严重时会造成人身伤害;特别是高速行驶的汽车,由于惯性,在刹车后很难立即停下,还要向前运动一段距离,这样往往会导致车祸的发生。为了避免悲剧的发牛,人们采用了很多应对方法。如为了防止汽车在突然刹车或突然减速时对人造成伤害,强制司乘人员使用安全带,并存汽车上安装安全气囊;另外还对汽车的行驶速度做出了限制。我国的交通法规明确规定:机动车行驶时在没有道路中心线的城市道路速度不能超过30km/h,公路上不能超过40km/h;在同方向只有l条机动车道的城市道路不能超过50km/h,公路上不能超过70km/h。需要说明的是,这些方法虽然都能减小惯性带来的危害,但是却并不能从根本上减小惯性。要真正地减小惯性就要减小物体的质量,针对当前我国运输业超载现象非常普遍的情况,有关部门做出规定:公路客运车辆载客超过额定乘员,货运车辆超过核定承载重量的,会处以相应的经济处罚,严重的还会扣留机动车。这是因为对载重汽车进行限载,既可以减小它对地面的压强,又能减小它的惯性,从而降低车祸的发生率。
重力的计算公式:
物体所受的重力跟它的质量成正比,g=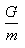 ,G=mg。(g=9.8N/g)
,G=mg。(g=9.8N/g)
重力与质量的区别和联系:
重力加速度:
重力加速度g的方向总是竖直向下的。在同一地区的同一高度,任何物体的重力加速度都是相同的。重力加速度的数值随海拔高度增大而减小。当物体距地面高度远远小于地球半径时,g变化不大。而离地面高度较大时,重力加速度g数值显著减小,此时不能认为g为常数。
距离地面同一高度的重力加速度,也会随着纬度的升高而变大。由于重力是万有引力的一个分力,万有引力的另一个分力提供了物体绕地轴作圆周运动所需要的向心力。物体所处的地理位置纬度越高,圆周运动轨道半径越小,需要的向心力也越小,重力将随之增大,重力加速度也变大。地理南北两极处的圆周运动轨道半径为0,需要的向心力也为0,重力等于万有引力,此时的重力加速度也达到最大。
物体所受的重力跟它的质量成正比,g=
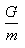 ,G=mg。(g=9.8N/g)
,G=mg。(g=9.8N/g)重力与质量的区别和联系:
| 质量 | 重力 | ||
| 区别 | 概念 | 物体所含物质的多少 | 由于地球吸引而使物体受到的力 |
| 符号 | m | G | |
| 量性 | 只有大小,没有方向 | 既有大小,又有方向 | |
| 单位 | 千克(kg) | 牛顿(N) | |
| 与地理位置的关系 | 与位置无关 | 与位置有关 | |
| 公式 | m=ρV | G=mg | |
| 测量工具 | 天平 | 测力计 | |
| 联系 | 重力与质量的关系是G=mg(g=9.8N/kg) | ||
重力加速度:
重力加速度g的方向总是竖直向下的。在同一地区的同一高度,任何物体的重力加速度都是相同的。重力加速度的数值随海拔高度增大而减小。当物体距地面高度远远小于地球半径时,g变化不大。而离地面高度较大时,重力加速度g数值显著减小,此时不能认为g为常数。
距离地面同一高度的重力加速度,也会随着纬度的升高而变大。由于重力是万有引力的一个分力,万有引力的另一个分力提供了物体绕地轴作圆周运动所需要的向心力。物体所处的地理位置纬度越高,圆周运动轨道半径越小,需要的向心力也越小,重力将随之增大,重力加速度也变大。地理南北两极处的圆周运动轨道半径为0,需要的向心力也为0,重力等于万有引力,此时的重力加速度也达到最大。
发现相似题
与“建设中的洋浦跨海大桥全长3.3km ,汽车行驶速度按 80km/h 设...”考查相似的试题有:
- 为开辟新航道,某科学家探测船装有回声探测仪器,探测水下有无暗礁,已知探测船发出的声音信号经0.6s被探测器接收到.(1)探...
- 一列长250m的列车,以54km/h的速度通过一座山洞,历时170s,那么山洞的长度是多少?
- 如图所示,可以表示同一种运动规律的图象是 ( ) A.甲 乙 B.乙 丙 C.甲 丁 D.乙 丁
- 长10m的平板车完全通过90m的大桥需要5s的时间,以同样的速度通过180m的大桥需要时间______s。
- 2011年“十一黄金周”期间小明和爸爸去曲阜“三孔”旅游,如图是他们乘坐出租车到达目的地时的出租车专用发票.(1)则出租车在该...
- 如图所示,用此装置拉一重为100N的重物,使其在地面上做匀速直线运动,若不计滑轮的摩擦和滑轮重,所需拉力为8N,则物体与地...
- 下列现象不是利用惯性的是[ ]A.跳远助跑跳得越远B.用力将物体抛出后物体最终会落到地面上C.子弹离开枪口后仍能继续向前飞行D....
- 人类已进入信息时代,很多信息给我们的生活和学习带来了 便利,但也存在一些伪信息,我们应当学会鉴别真假.(1)下面是一则...
- 一座限重为4.9×104N的桥,一辆自身质量为1.1t的卡车要能安全过桥,所能装载的货物不能超过 kg.
- 世界上最大的鸟是鸵鸟,它的重力为1470N,则它的质量______ kg,合______g;世界上最小的鸟是蜂鸟,若一只蜂鸟的质量是2000mg...