本试题 “摆角为θ的圆锥摆所受的向心力大小是( ) [ ] A.mgB.mgsinθC.mgcosθD.mgtanθ” 主要考查您对向心力
圆锥摆
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向心力
- 圆锥摆
向心力的定义:
在圆周运动中产生向心加速度的力。![]() 。
。
向心力的特性:
1、向心力
总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小,大小![]() ,方向总是指向圆心(与线速度方向垂直),方向时刻在变化,是一个变力。向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供。
,方向总是指向圆心(与线速度方向垂直),方向时刻在变化,是一个变力。向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供。
2、轻绳模型
Ⅰ、轻绳模型的特点:
①轻绳的质量和重力不计;
②可以任意弯曲,伸长形变不计,只能产生和承受沿绳方向的拉力;
③轻绳拉力的变化不需要时间,具有突变性。
Ⅱ、轻绳模型在圆周运动中的应用
小球在绳的拉力作用下在竖直平面内做圆周运动的临界问题:
①临界条件:小球通过最高点,绳子对小球刚好没有力的作用,由重力提供向心力:
②小球能通过最高点的条件: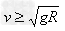 (当时
(当时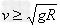 ,绳子对球产生拉力)
,绳子对球产生拉力)
③不能通过最高点的条件: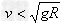 (实际上小球还没有到最高点时,就脱离了轨道)
(实际上小球还没有到最高点时,就脱离了轨道)
3、轻杆模型:
Ⅰ、轻杆模型的特点:
①轻杆的质量和重力不计;
②任意方向的形变不计,只能产生和承受各方向的拉力和压力;
③轻杆拉力和压力的变化不需要时间,具有突变性。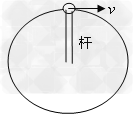
Ⅱ、轻杆模型在圆周运动中的应用
轻杆的一端连着一个小球在竖直平面内做圆周运动,小球通过最高点时,轻杆对小球产生弹力的情况:
①小球能通过最高点的临界条件: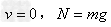 (N为支持力)
(N为支持力)
②当时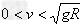 ,有
,有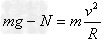 (N为支持力)
(N为支持力)
③当时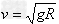 ,有
,有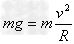 (N=0)
(N=0)
④当时 ,有
,有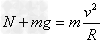 (N为拉力)
(N为拉力)
知识点拨:
向心力是从力的作用效果来命名的,因为它产生指向圆心的加速度,所以称它为向心力。它不是具有确定性质的某种类型的力。相反,任何性质的力都可以作为向心力。实际上它可是某种性质的一个力,或某个力的分力,还可以是几个不同性质的力沿着半径指向圆心的合外力。对一个物体进行受力分析的时候,是不需要画向心力的,向心力是效果力。
知识拓展:
对于向心力的理解,同学们可以切身的体会一下。两个同学手拉手,甲同学原地,乙同学绕着甲同学转,甲同学给乙同学的拉力就是向心力,当拉力大于向心力的时候,乙同学向心(甲同学)运动,当拉力小于向心力的时候,乙同学做离心运动。
圆锥摆的知识:
圆锥摆模型的结构特点——一根质量和伸长可以不计的线,系一个可以视为质点的摆球,在水平面内做匀速圆周运动,且在摆线沿顶点位置不变的圆锥面上运动。
圆锥摆的特点:
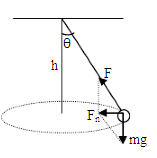
1、圆锥摆模型的受力特点——只受两个力:竖直向下的重力(mg)和沿摆线方向的拉力(F),二力的合力就是摆球做圆周运动的向心力(Fn),如图所示。
2、向心力和向心加速度的计算
设摆球的质量为m,摆长为l,与竖直方向的夹角为θ,摆球的线速度、角速度、周期和频率依次为v、ω、T和f。如图所示,根据不同的条件
向心力可以表示为: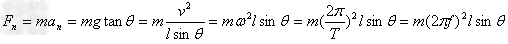 ;
;
向心加速度可表示为: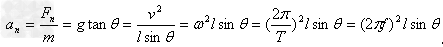 。
。
3、摆线拉力的计算计算
摆线的拉力,有两种基本思路:
①当θ角已知时,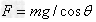 ;
;
②当θ角未知时,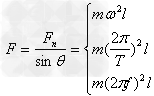 。
。
4、周期T、频率f和角速度ω的计算
根据向心加速度公式,有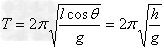 ,
,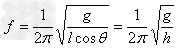 ,
, 。式中
。式中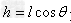 为摆球的轨道平面到悬点的距离,即圆锥摆的高度。由这些公式可知,高度相同的圆锥摆,即等高圆锥摆的T、f和ω相等,与m、l和θ无关。
为摆球的轨道平面到悬点的距离,即圆锥摆的高度。由这些公式可知,高度相同的圆锥摆,即等高圆锥摆的T、f和ω相等,与m、l和θ无关。
5、漏斗摆:物体在光滑的漏斗形容器内壁的某水平面上做匀速圆周运动。漏斗摆的力学特点:物体只受两个力,竖直向下的重力mg,垂直于漏斗壁的弹力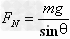 ,两个力的合力水平指向转轴,其向心力
,两个力的合力水平指向转轴,其向心力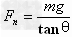 。如图所示。
。如图所示。
①向心加速度的计算 ,θ角一定,故an恒定。
,θ角一定,故an恒定。
②周期T、角速度ω、线速度v的计算(设匀速圆周运动的平面离漏斗尖端距离为h)
由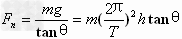 ,得
,得 ;
;
由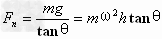 ,得
,得 ;
;
由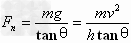 ,得
,得 。
。
可见,h增大,线速度增大,角速度减小,周期增大。
结构特点:
一根质量和伸长可以不计的线,系一个可以视为质点的摆球,在水平面内作匀速圆周运动。
受力特点:
只受两个力:竖直向下的重力 mg 和沿摆线方向的拉力 F 。两个力的合力,就是摆球作圆周运动的向心力 F n
与“摆角为θ的圆锥摆所受的向心力大小是( ) [ ] A.mgB.mgsinθC...”考查相似的试题有:
- 如图所示,已知,它们与轴的距离关系是,三物体与转盘表面的动摩擦因数相同,设最大静摩擦力等于滑动摩擦力,当转盘的转速逐...
- 如图所示,一木块放于水平转盘上,与转轴的距离为r,若木块与盘面间的最大静摩擦力是木块重力的μ倍,为使木块不与转盘发生相...
- 氢原子半径是0.53 ×10-10m ,根据卢瑟福的原子模型,求:(1) 电子所在轨道的电场强度;(2) 电子绕核运动的速率、频率.
- 一物块沿着圆弧下滑,由于摩擦作用,它的速率恰好保持不变,那么在下滑过程中下列说法正确的是( ) A.物块的加速度为零,合...
- 如图所示,MDN为绝缘材料制成的光滑竖直半圆环,半径为R,所处空间有磁感应强度为B的匀强磁场,方向垂直纸面向外。一带电量为...
- 如图所示,一个小球(视为质点)从H=12m高处,由静止开始通过光滑弧形轨道AB,进入半径R=4m的竖直圆环,且圆环动摩擦因数处处...
- 带电粒子在垂直于匀强磁场的平面内做匀速圆周运动,现欲缩短其旋转周期,可行的方案是( )A.减小粒子的入射速率B.减小磁感...
- 回旋加速器以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为d,两侧为相同匀强磁场,方向垂直纸面向里.一质...
- 在如图所示的竖直向下的匀强电场中,用绝缘的细线拴住的带电小球在竖直平面内绕悬点O做圆周运动,下列说法正确的是( )A.带...
- 图中,杂技演员在表演水流星节目时,盛水的杯子在竖直平面内做圆周运动,当杯子经过最高点时,里面的水也不会流出来,这是因...