本试题 “从静止开始做匀加速直线运动的物体,第1s 内通过的位移为0.3m,则( ) A.第ls末的速度为0.3m/s B.第2s内通过的位移是1.2m C.加速度为0.6m/s2 D.前2s内的...” 主要考查您对平均速度和瞬时速度的区别
匀变速直线运动规律的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 平均速度和瞬时速度的区别
- 匀变速直线运动规律的应用
平均速度:
质点在某段时间内的位移与发生这段位移所用时间的比值叫做这段时间(或位移)的平均速度v,即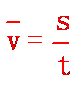 ,平均速度是矢量,其方向跟位移方向相同.平均速度是对变速运动的粗略描述。
,平均速度是矢量,其方向跟位移方向相同.平均速度是对变速运动的粗略描述。
瞬时速度:
运动物体在某一时刻(或经过某一位置)的速度,方向沿轨迹上质点所在点的切线方向指向前进的一侧,瞬时速度是对变速运动的精确描述,其大小叫速率。
平均速率:
物体在某段时间内通过的路程l跟通过这段路程所用的时间t的比值,叫做这段路程(或这段时间)的平均速率,即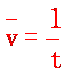 ,它是标量,值得注意的是:它并不是平均速度的大小.
,它是标量,值得注意的是:它并不是平均速度的大小.
平均速度和瞬时速度对比:
(1)区别:平均速度反映的是物体在整个运动过程中的整体运动情况,而瞬时速度反映的是物体在运动过程的某一时刻或某一位置的运动情况;
(2)联系:在匀速直线运动中,任何时刻的瞬时速度和整个运动过程中的平均速度相同。
方法与知识感悟:
平均速度是反映的某一段运动过程中的平均运动快慢,是这一过程中的位移与时间的比值( 是平均速度的定义式),适用于所有的运动;而
是平均速度的定义式),适用于所有的运动;而 适用于匀变速直线运动,但若
适用于匀变速直线运动,但若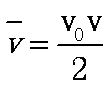 ,却不能判定该物体做匀变速直线运动.
,却不能判定该物体做匀变速直线运动.
平均速度的计算:
一辆汽车沿平直公路行驶,先以速度v1通过前的位移,再以速度v2=50km/h通过其余的位移.若整个位移中的平均速度=37.5km/h,则第一段位移内的平均速度是多少?
解:设整段位移为x,通过前位移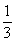 和后位移
和后位移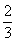 的时间分别为t和t
的时间分别为t和t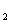 ,根据
,根据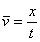 得
得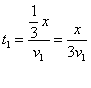 ,
,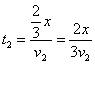 ,可得
,可得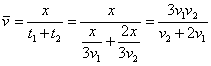 。解得第一段时间位移内的速度
。解得第一段时间位移内的速度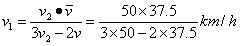 =25km/h。
=25km/h。
基本公式:
①速度公式:vt=v0+at;
②位移公式:s=v0t+ at2;
at2;
③速度位移公式:vt2-v02=2as。
推导公式:
①平均速度公式:V=![]() 。
。
②某段时间的中间时刻的瞬时速度等于该段时间内的平均速度:![]() 。
。
③某段位移的中间位置的瞬时速度公式:![]() 。无论匀加速还是匀减速,都有
。无论匀加速还是匀减速,都有![]() 。
。
④匀变速直线运动中,在任意两个连续相等的时间T内的位移差值是恒量,即ΔS=Sn+l–Sn=aT2=恒量。
⑤初速为零的匀变速直线运动中的比例关系(设T为相等的时间间隔,s为相等的位移间隔):
Ⅰ、T末、2T末、3T末……的瞬时速度之比为:v1:v2:v3:……:vn=1:2:3:……:n;
Ⅱ、T内、2T内、3T内……的位移之比为:s1:s2:s3:……:sn=1:4:9:……:n2;
Ⅲ、第一个T内、第二个T内、第三个T内……的位移之比为:sⅠ:sⅡ:sⅢ:……:sN=1:3:5:……:(2N-1);
Ⅳ、前一个s、前两个s、前三个s……所用的时间之比为:t1:t2:t3:……:tn=1:![]() ……:
……:![]() ;
;
Ⅴ、第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ:……:tN=1:![]() ……:
……:![]() 。
。
追及相遇问题:
①当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距会越来越大或越来越小,这时就会涉及追及、相遇或避免碰撞等问题。
②追及问题的两类情况:
Ⅰ、速度大者减速(如匀减速直线运动)追速度小者(如匀速运动): 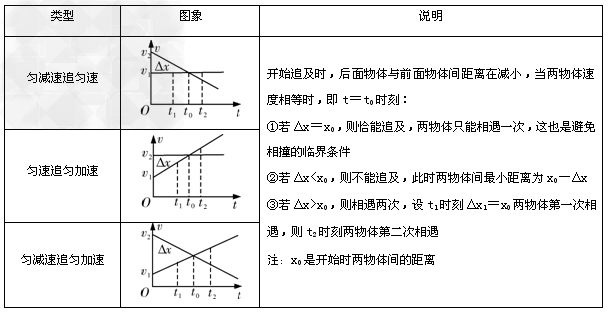
Ⅱ、速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动):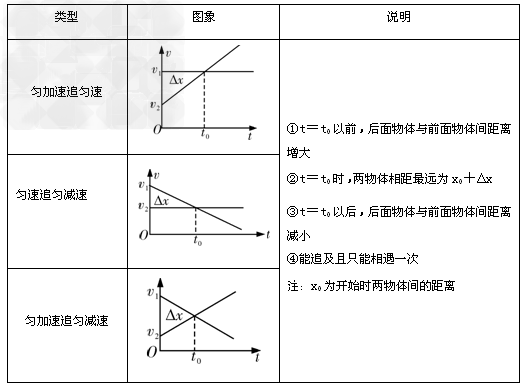
③相遇问题的常见情况:
Ⅰ、同向运动的两物体追及即相遇;
Ⅱ、相向运动的物体,当各自发生的位移大小和等于开始时两物体的距离时即相遇。
知识点拨:
例:如图所示,光滑斜面AE被分为四个长度相等的部分,即AB=BC=CD=DE,一物体由A点静止释放,下列结论不正确的是( )
A. 物体到达各点的速率之比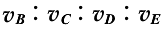 =
=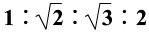 。
。
B. 物体到达各点所经历的时间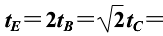
 。
。
C. 物体从A运动到E的全过程的平均速度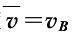 。
。
D. 物体通过每一部分时,其速度增量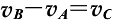
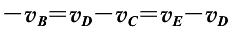 。
。
解析:由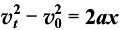 及
及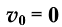 得
得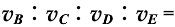
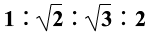 ,即A正确。由
,即A正确。由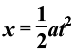 得
得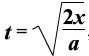 ,则
,则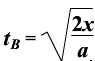 ,
, ,
,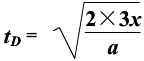 ,
,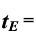
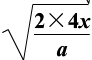 ,由此可知B正确。由
,由此可知B正确。由 得
得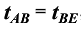 ,即B点为AE段的时间中点,故
,即B点为AE段的时间中点,故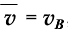 ,即C正确。对于匀变速直线运动,若时间相等,速度增量相等,故D错误,只有D符合题意。
,即C正确。对于匀变速直线运动,若时间相等,速度增量相等,故D错误,只有D符合题意。
答案:D
与“从静止开始做匀加速直线运动的物体,第1s 内通过的位移为0.3m...”考查相似的试题有:
- 不定项选择物体沿一条直线运动,下列说法中正确的有( )A.物体在某时刻的速度为3 m/s,则物体在1 s内一定走3 m B.物体在某...
- 一个物体做单向直线运动,它走完前半程的平均速度是12m/s,走完后半程的平均速度是6m/s,则它在全程的平均速度是( )A.12m/...
- 汽车刹车后作匀减速直线运动,最后停下来,在刹车过程中,汽车前半程的平均速度与后半程的平均速度之比是( )A.(2+1):1B....
- 汽车在两车站间沿直线行驶时,从甲站出发,先以速度v匀速行驶了全程的一半,接着匀减速行驶后一半路程,抵达乙车站时速度恰好...
- 刘翔冲刺终点撞线时的速度,是平均速度还是瞬时速度?
- 人类在探索自然规律的过程中总结了许多科学方法,如控制变量法、比值定义法、极限法等.在下列研究中,可以用极限法的是( )...
- 物体先做初速为零的匀加速运动,加速度为a1,当速度达到v时,改为以a2作匀减速运动直至速度为零,在加速和减速过程中,物体的...
- 某质点作直线运动,速度随时间的变化的关系式为v=(2t+ 4)m/s ,则对这个质点运动描述,正确的是A.初速度为4 m/sB.加速度...
- 为了安全,在公路上行驶的汽车之间应保持必要的距离。已知某公路的最高限速v=" 72" km/h。假设前方车辆突然停止,后车司机从...
- 我国是一个能源消耗大国,节约能源刻不容缓。设有一架直升飞机以加速度a从地面由静止开始竖直向上起飞,已知飞机在上升过程中...