本试题 “【选修3-4选做题】有一弹簧振子在水平方向上的BC之间做简谐运动,已知BC间的距离为20cm,振子在2s内完成了10次全振动。若从某时刻振子经过平衡位置时开始计时...” 主要考查您对简谐运动的图像
简谐运动的振幅
简谐运动的周期、频率和角频率
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 简谐运动的图像
- 简谐运动的振幅
- 简谐运动的周期、频率和角频率
1、意义:表示振动物体位移随时间变化的规律,注意振动图像不是质点的运动轨迹。
2、特点:简谐运动的图像是正弦(或余弦)曲线。
3、应用:可直观地读取振幅A、周期T以及各时刻的位移x,判定回复力、加速度方向,判定某段时间内位移、回复力、加速度、速度、动能、势能的变化情况。
简谐运动图像问题的解法:
简谐运动图像能够反映简谐运动的运动规律,因此将简谐运动图像跟具体的运动过程联系起来是讨论简谐运动的一种好方法。
①从简谐运动图像可以直接读出不同时刻t的位移值,从而知道位移x随时间£的变化情况。
②在简谐运动图像中,用作曲线上某点切线的办法可确定各时刻质点的速度大小和方向。当切线与x 轴正方向的夹角小于90。时,速度方向与选定的正方向相同,且夹角越大表明此时速度越大;当切线与x轴正方向的夹角大于90。时,速度方向与选定的正方向相反,且夹角越大表明此时速度越小。也可以根据位移情况来判断速度的大小。因为质点离平衡位置越近,质点速度越大,而最大位移处,质点速度为零。根据位移变化趋势判定速度方向,若正位移增大,速度为正方向,若正位移减小,速度为负方向;反之,若负位移增大,速度为负方向,若负位移减小,速度为正方向。
③由于 ,故可以根据图像上各个时刻的 位移变化情况确定质点加速度的变化情况。同样,只要知道了位移和速度的变化情况,也就不难判断出质点在不同时刻的动能和势能的变化情况。
,故可以根据图像上各个时刻的 位移变化情况确定质点加速度的变化情况。同样,只要知道了位移和速度的变化情况,也就不难判断出质点在不同时刻的动能和势能的变化情况。
振动物体离开平衡位置的最大距离,是标量,表示振动的强弱。
周期T和频率f:
1.意义:表示振动快慢的物理量,周期越短,频率越高,振动越快
2.定义:
完成一次全振动所需要的时间,用T表示
单位时间内完成全振动的次数,用f表示
3.关系:Tf=1
4.决定因素:周期与频率由振动系统本身决定,与振幅无关
5.角频率ω:ω=2πf。
应用简谐运动的对称性及周期性的解题方法:
如图所示, 物体在A与B间运动,O点为平衡位置,C和D两点关于O点对称,则有:
物体在A与B间运动,O点为平衡位置,C和D两点关于O点对称,则有:
1.时间的对称性 
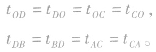
2.速度的对称性
(1)物体连续两次经过同一点(如D点)的速度大小相等,方向相反。
(2)物体经过关于D点对称的两点(如C与D两点)的速度大小相等,方向可能相同,也可能相反。
3.周期性简谐运动是一种周而复始的周期性的运动,按其周期性可作如下判断:
(1)若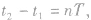 则
则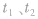 两时刻振动物体在同一位置,运动情况相同。
两时刻振动物体在同一位置,运动情况相同。
(2)若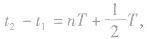 则
则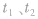 两时刻,描述运动的物理量
两时刻,描述运动的物理量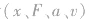 均大小相等,方向相反。
均大小相等,方向相反。
(3)若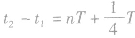 或
或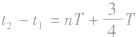 ,则当
,则当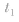 时刻物体在最大位移处时,
时刻物体在最大位移处时,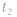 时刻物体到达平衡位置;当t1时刻物体在平衡位置时,t2时刻物体到达最大位移处;若t1时刻物体在其他位置,t2时刻物体到达何处就要视具体情况而定。
时刻物体到达平衡位置;当t1时刻物体在平衡位置时,t2时刻物体到达最大位移处;若t1时刻物体在其他位置,t2时刻物体到达何处就要视具体情况而定。
与“【选修3-4选做题】有一弹簧振子在水平方向上的BC之间做简谐运...”考查相似的试题有:
- 如图11-2-9所示,放在光滑水平面上的弹簧振子,振子质量为m,振子以O为平衡位置,在B和C之间振动,设振子经平衡位置时的速度...
- 劲度系数为20N/cm的弹簧振子,它的振动图象如图所示,在图中A点对应的时刻[ ]A.振子所受的弹力大小为5N,方向指向x轴的负方...
- 如图所示,是一列沿x轴正向传播的简谐横波在t时刻的图象。已知x轴上3cm处的质点P在Δt=t/-t=0.35s内通过的路程为14cm.则( )A...
- 图l是一列简谐横波在t=1.25s时的波形图,已知c位置的质点比a位置的晚0.5s起振,则图2所示振动图象对应的质点可能位于( )A....
- 一列沿x轴正向传播的横波在某时刻的波形图如图甲所示,a、b、c、d为介质中沿波的传播方向上四个质点的平衡位置,若从该时刻开...
- 一个弹簧振子在光滑的水平面上作简谐运动,其中有两个时刻弹簧对振子的弹力大小相等,但方向相反,那么这两个时刻弹簧振子的...
- 一个水平放置的弹簧振子在A、B两点间做简谐运动,O为平衡位置,如图所示.设水平向右方向为正方向,以某一时刻作计时起点(t=...
- 一水平弹簧振子的质量为100g,频率为5Hz,若把振子拉开4cm后放开,弹簧的劲度系数为100N/m,求:(1)弹簧振子的最大加速度大...
- 做简谐振动的质点每次经过同一位置时,不相同的物理量是( ) A.速度 B.位移 C.动能 D.加速度
- 下列物理量中能够反映物体做机械振动强弱的物理量是( ) A.频率 B.振幅 C.回复力 D.周期