本试题 “(A)某天文台测得某行星的一颗卫星绕行星做匀速圆周运动,测得其轨道半径为R,周期为T,则其向心加速度为______;行星的质量为______.(万有引力恒量为G)...” 主要考查您对匀变速直线运动的位移与时间的关系
人造地球卫星
万有引力定律的其他应用
牛顿第二定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 匀变速直线运动的位移与时间的关系
- 人造地球卫星
- 万有引力定律的其他应用
- 牛顿第二定律
匀变速直线运动的位移公式:
由平均速度的定义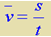 和匀变速直线运动的平均速度
和匀变速直线运动的平均速度 及速度公式
及速度公式 ,联立推导出匀变速直线运动的位移公式:
,联立推导出匀变速直线运动的位移公式: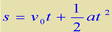
知识点拨:
1、是匀变速直线运动位移的一般表示形式.它能表明质点在各个时刻相对初始时刻(t=0)的位移。
2、在位移公式中s、v0、a均是矢量,解题时一般要选取v0方向为正。
3、位移公式可由速度图象来推导,
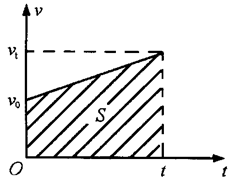
如图是某物体做匀变速直线运动的图象.根据图象的物理意义,它与横轴(时间轴)所围的那块梯形面积表示运动的位移.所以: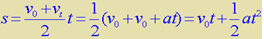
人造地球卫星:
在地球上抛出的物体,当它的速度足够大时,物体就永远不会落到地面上,它将围绕地球旋转,成为一颗人造地球卫星,简称人造卫星。
(1)人造卫星按运行轨道可分为低轨道卫星、中轨道卫星、高轨道卫星,以及地球同步轨道卫星、极地轨道卫星等。
(2)按用途人造卫星可分为三大类:科学卫星、技术试验卫星和应用卫星。
人造地球卫星:
1、若已知人造卫星绕地心做匀速率圆周运动的轨道半径为r,地球的质量为M,各物理量与轨道半径的关系:
①由![]() 得卫星运行的向心加速度为:
得卫星运行的向心加速度为:![]() ;
;
②由![]() 得卫星运行的线速度为:
得卫星运行的线速度为:![]() ;
;
③由![]() 得卫星运行的角速度为:
得卫星运行的角速度为: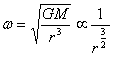 ;
;
④由 得卫星运行的周期为:
得卫星运行的周期为: ;
;
⑤由![]() 得卫星运行的动能:
得卫星运行的动能:![]() ;
;
即随着运行的轨道半径的逐渐增大,向心加速度a、线速度v、角速度ω、动能Ek将逐渐减小,周期T将逐渐增大。
2、用万有引力定律求卫星的高度:
通过观测卫星的周期T和行星表面的重力加速度g及行星的半径R可以求出卫星的高度。
3、近地卫星、赤道上静止不动的物体
①把在地球表面附近环绕地球做匀速率圆周运动的卫星称之为近地卫星,它运行的轨道半径可以认为等于地球的半径R0,其轨道平面通过地心。若已知地球表面的重力加速度为g0,则
由![]() 得:
得:![]() ;
;
由![]() 得:
得: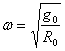 ;
;
由![]() 得:
得: 。
。
若将地球半径R0=6.4×106m和g0=9.8m/s2代入上式,可得v=7.9×103m/s,ω=1.24×10-3rad/s,T=5074s,由于![]() ,
, 和
和 且卫星运行的轨道半径 r>R0,所以所有绕地球做匀速率圆周运动的卫星线速度v<7.9×103m/s,角速度ω<1.24×10-3rad/s,而周期T>5074s。
且卫星运行的轨道半径 r>R0,所以所有绕地球做匀速率圆周运动的卫星线速度v<7.9×103m/s,角速度ω<1.24×10-3rad/s,而周期T>5074s。
②特别需要指出的是,静止在地球表面上的物体,尽管地球对物体的重量也为mg,尽管物体随地球自转也一起转,绕地轴做匀速率圆周运动,且运行周期等于地球自转周期,与近地卫星、同步卫星有相似之处,但它的轨道平面不一定通过地心,如图所示。只有当纬度θ=0°,即物体在赤道上时,轨道平面才能过地心.地球对物体的引力F的一个分力是使物体做匀速率圆周运动所需的向心力f=mω2r,另一个分力才是物体的重量mg,即引力F不等于物体的重量mg,只有当r=0时,即物体在两极处,由于f=mω2r=0,F才等于mg。
③赤道上随地球自转而做圆周运动的物体与近地卫星的区别:
A、赤道上物体受的万有引力只有一小部分充当向心力,另一部分作为重力使得物体紧压地面,而近地卫星的引力全部充当向心力,卫星已脱离地球;
B、赤道上(地球上)的物体与地球保持相对静止,而近地卫星相对于地球而言处于高速旋转状态。
4、卫星的超重和失重
“超重”是卫星进入轨道的加速上升过程和回收时的减速下降过程,此情景与“升降机”中物体超重相同。“失重”是卫星进入轨道后正常运转时,卫星上的物体完全“失重”(因为重力提供向心力),此时,在卫星上的仪器,凡是制造原理与重力有关的均不能正常使用,比如水银气压计、天平、密度计、电子称、摆钟等。
5、卫星变轨问题
卫星由低轨道运动到高轨道,要加速,加速后作离心运动,势能增大,动能减少,到高轨道作圆周运动时速度小于低轨道上的速度。 
当以第一宇宙速度发射人造卫星,它将围绕地球表面做匀速圆周运动;若它发射的速度介于第一宇宙速度与第二宇宙速度之间,则它将围绕地球做椭圆运动。有时为了让卫星绕地球做圆周运动,要在卫星发射后做椭圆运动的过程中二次点火,以达到预定的圆轨道。设第一宇宙速度为v,则由第一宇宙速度的推导过程有![]() 。在地球表面若卫星发射的速度v1>v,则此时卫星受地球的万有引力
。在地球表面若卫星发射的速度v1>v,则此时卫星受地球的万有引力![]() 应小于卫星以v1绕地表做圆周运动所需的向心力m
应小于卫星以v1绕地表做圆周运动所需的向心力m![]() ,故从此时开始卫星将做离心运动,在卫星离地心越来越远的同时,其速率也要不断减小,在其椭圆轨道的远地点处(离地心距离为R′),速率为v2(v2<v1),此时由于G>m
,故从此时开始卫星将做离心运动,在卫星离地心越来越远的同时,其速率也要不断减小,在其椭圆轨道的远地点处(离地心距离为R′),速率为v2(v2<v1),此时由于G>m![]() ,卫星从此时起做向心运动,同时速率增大,从而绕地球沿椭圆轨道做周期性的运动。如果在卫星经过远地点处开动发动机使其速率突然增加到v3,使G=m,则卫星就可以以速率v3,以R′为半径绕地球做匀速圆周运动。同样的道理,在卫星回收时,选择恰当的时机使做圆周运动的卫星速率突然减小,卫星将会沿椭圆轨道做向心运动,让该椭圆与预定回收地点相切或相交,就能成功地回收卫星。
,卫星从此时起做向心运动,同时速率增大,从而绕地球沿椭圆轨道做周期性的运动。如果在卫星经过远地点处开动发动机使其速率突然增加到v3,使G=m,则卫星就可以以速率v3,以R′为半径绕地球做匀速圆周运动。同样的道理,在卫星回收时,选择恰当的时机使做圆周运动的卫星速率突然减小,卫星将会沿椭圆轨道做向心运动,让该椭圆与预定回收地点相切或相交,就能成功地回收卫星。
万有引力定律的其他应用:
万有引力定律: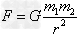 (G=6.67×10-11 N·m2/kg2),万有引力定律在天文学中的应用:
(G=6.67×10-11 N·m2/kg2),万有引力定律在天文学中的应用:
1、计算天体的质量和密度;
2、人造地球卫星、地球同步卫星、近地卫星;
3、发现未知天体;
4、分析重力加速度g随离地面高度h的变化情况;
①物体的重力随地面高度h的变化情况:物体的重力近似地球对物体的吸引力,即近似等于 ,可见物体的重力随h的增大而减小,由G=mg得g随h的增大而减小。
,可见物体的重力随h的增大而减小,由G=mg得g随h的增大而减小。
②在地球表面(忽略地球自转影响):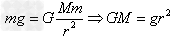 (g为地球表面重力加速度,r为地球半径)。
(g为地球表面重力加速度,r为地球半径)。
③当物体位于地面以下时,所受重力也比地面要小,物体越接近地心,重力越小,物体在地心时,其重力为零。
5、双星问题:天文学上把两颗相距比较近,又与其他星体距离比较远的星体叫做双星。双星的间距是一定的,它们绕二者连线上的同一点分别做圆周运动,角速度相等。以下图为例

由以上各式解得: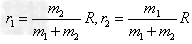
6、黄金代换公式:GM=gR2。
物体的加速度跟所受的外力的合力成正比,跟物体的质量成反比,加速度的方向跟合外力的方向相同,表达式F=kma。在国际单位制中,k=1,上式简化为F合=ma。牛顿这个单位就是根据牛顿第二定律定义的:使质量是1kg的物体产生1m/s2加速度的力,叫做1N(kg·m/s2=N)。
对牛顿第二定律的理解:
①模型性
牛顿第二定律的研究对象只能是质点模型或可看成质点模型的物体。
②因果性
力是产生加速度的原因,质量是物体惯性大小的量度,物体的加速度是力这一外因和质量这一内因共同作用的结果。
③矢量性
合外力的方向决定了加速度的方向,合外力方向变,加速度方向变,加速度方向与合外力方向一致。其实牛顿第二定律的表达形式就是矢量式。
④瞬时性
加速度与合外力是瞬时对应关系,它们同生、同灭、同变化。
⑤同一性(同体性)
 中各物理量均指同一个研究对象。因此应用牛顿第二定律解题时,首先要处理好的问题是研究对象的选择与确定。
中各物理量均指同一个研究对象。因此应用牛顿第二定律解题时,首先要处理好的问题是研究对象的选择与确定。⑥相对性
在
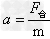 中,a是相对于惯性系的而不是相对于非惯性系的,即a是相对于没有加速度参照系的。
中,a是相对于惯性系的而不是相对于非惯性系的,即a是相对于没有加速度参照系的。⑦独立性
F合产生的加速度a是物体的总加速度,根据矢量的合成与分解,则有物体在x方向的加速度ax;物体在y方向的合外力产生y方向的加速度ay。牛顿第二定律分量式为:
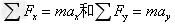 。
。⑧局限性(适用范围)
牛顿第二定律只能解决物体的低速运动问题,不能解决物体的高速运动问题,只适用于宏观物体,不适用与微观粒子。
牛顿第二定律的应用:
1.应用牛顿第二定律解题的步骤:
(1)明确研究对象。可以以某一个质点作为研究对象,也可以以几个质点组成的质点组作为研究对象。设每个质点的质量为mi,对应的加速度为ai,则有:F合=
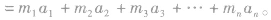
对这个结论可以这样理解:先分别以质点组中的每个质点为研究对象用牛顿第二定律:
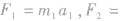
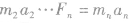 ,将以上各式等号左、右分别相加,其中左边所有力中,凡属于系统内力的,总是成对出现并且大小相等方向相反,其矢量和必为零,所以最后得到的是该质点组所受的所有外力之和,即合外力F。。
,将以上各式等号左、右分别相加,其中左边所有力中,凡属于系统内力的,总是成对出现并且大小相等方向相反,其矢量和必为零,所以最后得到的是该质点组所受的所有外力之和,即合外力F。。 (2)对研究对象进行受力分析,同时还应该分析研究对象的运动情况(包括速度、加速度),并把速度、加速度的方向在受力图旁边表示出来。
(3)若研究对象在不共线的两个力作用下做加速运动,一般用平行四边形定则(或三角形定则)解题;若研究对象在不共线的三个或三个以上的力作用下做加速运动,一般用正交分解法解题(注意灵活选取坐标轴的方向,既可以分解力,也可以分解加速度)。
(4)当研究对象在研究过程的小同阶段受力情况有变化时,那就必须分阶段进行受力分析,分阶段列方程求解。
2.两种分析动力学问题的方法:
(1)合成法分析动力学问题若物体只受两个力作用而产生加速度时,根据牛顿第二定律可知,利用平行四边形定则求出的两个力的合力方向就是加速度方向。特别是两个力互相垂直或相等时,应用力的合成法比较简单。
(2)正交分解法分析动力学问题当物体受到两个以上的力作用而产生加速度时,常用正交分解法解题。通常是分解力,但在有些情况下分解加速度更简单。
①分解力:一般将物体受到的各个力沿加速度方向和垂直于加速度方向分解,则:
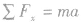 (沿加速度方向),
(沿加速度方向),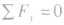 (垂直于加速度方向)。
(垂直于加速度方向)。 ②分解加速度:当物体受到的力相互垂直时,沿这两个相互垂直的方向分解加速度,再应用牛顿第二定律列方程求解,有时更简单。具体问题中要分解力还是分解加速度需要具体分析,要以尽量减少被分解的量,尽量不分解待求的量为原则。
3.应用牛顿第二定律解决的两类问题:
(1)已知物体的受力情况,求解物体的运动情况解这类题目,一般是应用牛顿运动定律求出物体的加速度,再根据物体的初始条件,应用运动学公式,求出物体运动的情况,即求出物体在任意时刻的位置、速度及运动轨迹。流程图如下:

(2)已知物体的运动情况,求解物体的受力情况解这类题目,一般是应用运动学公式求出物体的加速度,再应用牛顿第二定律求出物体所受的合外力,进而求出物体所受的其他外力。流程图如下:
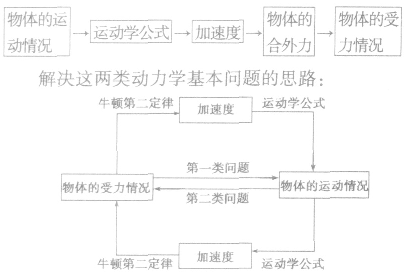
可以看出,在这两类基本问题中,应用到牛顿第二定律和运动学公式,而它们中间联系的纽带是加速度,所以求解这两类问题必须先求解物体的加速度。
知识扩展:
1.惯性系与非惯性系:牛顿运动定律成立的参考系,称为惯性参考系,简称惯性系。牛顿运动定律不成立的参考系,称为非惯性系。
2.关于a、△v、v与F的关系
(1)a与F有必然的瞬时的关系F为0,则a为0; F不为0,则a不为0,且大小为a=F/m。F改变,则a 立即改变,a和F之间是瞬时的对应关系,同时存在,同时消失.同时改变。
(2)△v(速度的改变量)与F有必然的但不是瞬时的联系 F为0,则△v为0;F不,0,并不能说明△v就一定不为0,因为
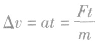 ,F不为0,而t=0,则△v=0,物体受合外力作用要有一段时间的积累,才能使速度改变。
,F不为0,而t=0,则△v=0,物体受合外力作用要有一段时间的积累,才能使速度改变。 (3)v(瞬时速度)与F无必然的联系 F为0时,物体可做匀速直线运动,v不为0;F不为0时,v可以为0,例如竖直上抛到达最高点时。
与“(A)某天文台测得某行星的一颗卫星绕行星做匀速圆周运动,测...”考查相似的试题有:
- 气球以10m/s的速度匀速竖直上升,从气球上掉下一个物体,经17s到达地面.物体刚脱离气球时气球的高度H=______M,到达地面的速...
- 小铁块置于长木板右端,木板放在光滑水平地面上,t=0时使二者获得等大反向的初速度开始运动,经过时间t1铁块在木板上停止滑动...
- 一个做初速度为零的匀加速直线运动的物体,它在4s内通过的位移是8m,则它的加速度为( )A.0.5m/s2B.1.0m/s2C.1.5m/s2D.2...
- 汽车以36km/h的速度在平直公路上匀速行驶,刹车后经2s速度变为21.6km/h,求:(1)刹车过程中的加速度;(2)刹车后8s内前进...
- 在光滑水平地面上,一物体静止.现受到水平拉力F的作用,拉力F随时间t变化的图象如图所示.则( )A.物体做往复运动B.0-4s...
- 我国和欧盟合作的“伽利略”卫星导航定位系统结束了美国全球卫星定位系统(GPS)一统天下的局面。该定位系统由30颗轨道卫星组成...
- 在讨论地球潮汐成因时,地球绕太阳运行轨道与月球绕地球运行轨道可视为圆轨道。已知太阳质量约为月球质量的2.7×107倍,地球绕...
- 斜面上的物体受到平行于斜面向下的力F作用,力F随时间变化的图象及物体运动的v-t图象,如图所示.由图象中的信息能够求出的量...
- 手托着一木块,由静止开始向上加速运动,手对木块的支持力应该( )A.小于木块对手的压力B.大于木块对手的压力C.等于木块...
- 下左图为某次实验中拍摄到的小滑块在粗糙水平面上滑动时的闪光照片.已知闪光频率为每秒l0次.当地重力加速度值为9.8m/s2,根...