本试题 “已知动圆S过点T(0,2)且被x轴截得的弦CD长为4。(1)求动圆圆心S的轨迹E的方程;(2)设P是直线l:y=x-2上任意一点,过P作轨迹E的切线PA,PB,A,B是切点,...” 主要考查您对导数的概念及其几何意义
直线的倾斜角与斜率
抛物线的标准方程及图象
直线与抛物线的应用
一元二次方程及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 导数的概念及其几何意义
- 直线的倾斜角与斜率
- 抛物线的标准方程及图象
- 直线与抛物线的应用
- 一元二次方程及其应用
平均变化率:
一般地,对于函数y =f(x),x1,x2是其定义域内不同的两点,那么函数的变化率可用式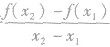 表示,我们把这个式子称为函数f(x)从x1到x2的平均变化率,习惯上用
表示,我们把这个式子称为函数f(x)从x1到x2的平均变化率,习惯上用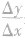 表示,即平均变化率
表示,即平均变化率
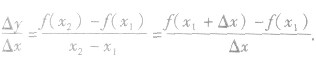
上式中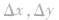 的值可正可负,但
的值可正可负,但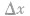 不为0.f(x)为常数函数时,
不为0.f(x)为常数函数时,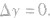
瞬时速度:
如果物体的运动规律是s=s(t),那么物体在时刻t的瞬时速度v就是物体在t到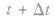 这段时间内,当
这段时间内,当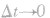 时平均速度的极限,即
时平均速度的极限,即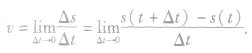
若物体的运动方程为s=f(t),那么物体在任意时刻t的瞬时速度v(t)就是平均速度v(t,d)为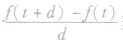 当d趋于0时的极限.
当d趋于0时的极限.
函数y=f(x)在x=x0处的导数的定义:
一般地,函数y=f(x)在x=x0处的瞬时变化率是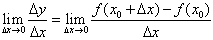 ,我们称它为函数y=f(x)在x=x0处的导数,记作
,我们称它为函数y=f(x)在x=x0处的导数,记作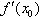 或
或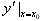 ,即
,即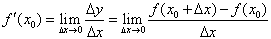 。
。
导函数:
如果函数y =f(x)在开区间(a,6)内的每一点都可导,则称在(a,b)内的值x为自变量,以x处的导数称为f(x为函数值的函数为fx)在(a,b)内的导函数,简称为f(x)在(a,b)内的导数,记作f′(x)或y′.即f′(x)=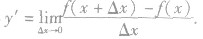
切线及导数的几何意义:
(1)切线:PPn为曲线f(x)的割线,当点Pn(xn,f(xn))(n∈N)沿曲线f(x)趋近于点P(x0,f(x0))时,割线PPn趋近于确定的位置,这个确定的位置的直线PT称为点P处的切线。
(2)导数的几何意义:函数f(x)在x=x0处的导数就是切线PT的斜率k,即k=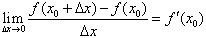 。
。
瞬时速度特别提醒:
①瞬时速度实质是平均速度当 时的极限值.
时的极限值.
②瞬时速度的计算必须先求出平均速度,再对平均速度取极限,
函数y=f(x)在x=x0处的导数特别提醒:
①当 时,比值
时,比值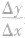 的极限存在,则f(x)在点x0处可导;若
的极限存在,则f(x)在点x0处可导;若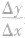 的极限不存在,则f(x)在点x0处不可导或无导数.
的极限不存在,则f(x)在点x0处不可导或无导数.
②自变量的增量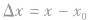 可以为正,也可以为负,还可以时正时负,但
可以为正,也可以为负,还可以时正时负,但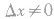 .而函数的增量
.而函数的增量 可正可负,也可以为0.
可正可负,也可以为0.
③在点x=x0处的导数的定义可变形为:

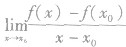
导函数的特点:
①导数的定义可变形为: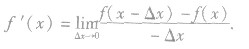
②可导的偶函数其导函数是奇函数,而可导的奇函数的导函数是偶函数,
③可导的周期函数其导函数仍为周期函数,
④并不是所有函数都有导函数.
⑤导函数 与原来的函数f(x)有相同的定义域(a,b),且导函数
与原来的函数f(x)有相同的定义域(a,b),且导函数 在x0处的函数值即为函数f(x)在点x0处的导数值.
在x0处的函数值即为函数f(x)在点x0处的导数值.
⑥区间一般指开区间,因为在其端点处不一定有增量(右端点无增量,左端点无减量).
导数的几何意义(即切线的斜率与方程)特别提醒:
①利用导数求曲线的切线方程.求出y=f(x)在x0处的导数f′(x);利用直线方程的点斜式写出切线方程为y-y0 =f′(x0)(x- x0).
②若函数在x= x0处可导,则图象在(x0,f(x0))处一定有切线,但若函数在x= x0处不可导,则图象在(x0,f(x0))处也可能有切线,即若曲线y =f(x)在点(x0,f(x0))处的导数不存在,但有切线,则切线与x轴垂直.
③注意区分曲线在P点处的切线和曲线过P点的切线,前者P点为切点;后者P点不一定为切点,P点可以是切点也可以不是,一般曲线的切线与曲线可以有两个以上的公共点,
④显然f′(x0)>0,切线与x轴正向的夹角为锐角;f′(x0)<o,切线与x轴正向的夹角为钝角;f(x0) =0,切线与x轴平行;f′(x0)不存在,切线与y轴平行.
直线的倾斜角的定义:
x轴正向与直线向上方向之间所成的角叫直线的倾斜角。特别地,当直线与x轴平行或重合时,我们规定它的倾斜角为0度。因此,倾斜角的取值范围是0°≤α<180°。
直线的斜率的定义:
倾斜角不是90°的直线,它的倾斜角的正切值叫做这条直线的斜率。直线的斜率常用k表示。即k=tanα。斜率反映直线与x轴的倾斜程度。
直线斜率的性质:
当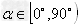 时,k≥0;当
时,k≥0;当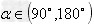 时,k<0;当
时,k<0;当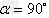 时,k不存在。
时,k不存在。
直线倾斜角的理解:
(1)注意“两个方向”:直线向上的方向、x轴的正方向;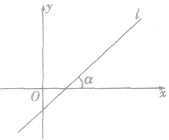
(2)规定当直线和x轴平行或重合时,它的倾斜角为0度。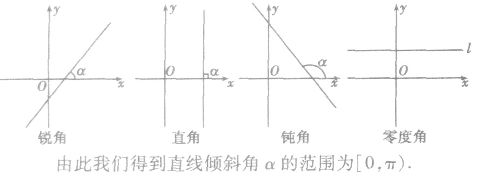
直线倾斜角的意义:
①直线的倾斜角,体现了直线对x轴正向的倾斜程度;
②在平面直角坐标系中,每一条直线都有一个确定的倾斜角;
③倾斜角相同,未必表示同一条直线。
直线斜率的理解:
每条直线都有倾斜角,但每条直线不一定都有斜率, 斜率不存在;当
斜率不存在;当 也逐渐增大;
也逐渐增大; 且逐渐增大。
且逐渐增大。
抛物线的标准方程及图像(见下表):

抛物线的标准方程的理解:
①抛物线的标准方程是指抛物线在标准状态下的方程,即顶点在原点,焦点在坐标轴上;
②抛物线的标准方程中的系数p叫做焦参数,它的几何意义是:焦点到准线的距离.焦点到顶点以及顶点到准线的距离均为
③抛物线的标准方程有四种类型,所以判断其类型是解题的关键,在方程的类型已确定的前提下,由于标准方程只有一个参数p,所以只需一个条件就可以确定一个抛物线的方程;
④对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,得出其异同点。
共同点:
a.原点在抛物线上;
b.焦点都在坐标轴上;
c.准线与焦点所在轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的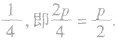
不同点:
a.焦点在x轴上时,方程的右侧为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2;
b.开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
求抛物线的标准方程的常用方法:
(1)定义法求抛物线的标准方程:定义法求曲线方程是经常用的一种方法,关键是理解定义的实质及注意条件,将所给条件转化为定义的条件,当然还应注意特殊情况.
(2)待定系数法求抛物线的标准方程:求抛物线标准方程常用的方法是待定系数法,为避免开口不确定,分成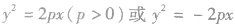 (p>0)两种情况求解的麻烦,可以设成
(p>0)两种情况求解的麻烦,可以设成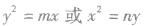 (m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
(m,n≠0),若m、n>0,开口向右或向上;m、n<0,开口向左或向下;m、n有两解,则抛物线的标准方程各有两个。
设直线l的方程为:Ax+By+C=0(A、B不同时为零),抛物线的方程为y2=2px(p>0),将直线的方程代入抛物线的方程,消去y(或x) 得到一元二次方程,进而应用根与系数的关系解题。
直线与抛物线的位置关系:
直线和抛物线的位置关系,可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定,同时注意过焦点的弦的一些性质,如:
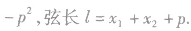
一元二次方程的定义:
含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:
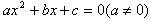 。
。
一元二次方程的应用:
建立一元二次方程模型进行求解,把得到的答案带回实际问题中检验是否合理,来解决实际问题,如打折、营销、增长率问题等。
一元二次方程的根与系数的关系:
如果方程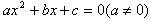 的两个实数根是
的两个实数根是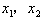 ,那么
,那么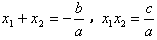 。
。
与“已知动圆S过点T(0,2)且被x轴截得的弦CD长为4。(1)求动圆...”考查相似的试题有:
- 曲线y=在点(1,2)处的切线为( ).
- 若存在过点(1,0)的直线与曲线y=x3和y=ax2+154x-9都相切,则a等于______.
- 设函数,且,,,下列命题:①若,则②存在,,使得③若,,则④对任意的,,都有其中正确的是_______________.(填写序号)
- 已知函数,(1)求函数在上的最小值;(2)若函数与的图像恰有一个公共点,求实数a的值;(3)若函数有两个不同的极值点,且...
- 一质点的运动方程为,该质点在时的瞬时速度 。
- 以100的速度向一气球中注入气体,如果气体的压强不变,气球的半径会逐渐增大,当半径增大到10时,气球半径增加的瞬时速度为__...
- 设直线的倾斜角为.(1)若,试求B的取值范围;(2)若,求的取值范围.
- 已知函数f(x)=axx2+b在x=1处取得极值2.(1)求函数f(x)的表达式;(2)当m满足什么条件时,函数f(x)在区间(m,2m+1)上...
- 设O是坐标原点,F是抛物线y2=2px(p>0)的焦点,A是抛物线上的一个动点,与x轴正方向的夹角为60°,求||的值.
- 设a>0,函数.(1)求证:关于x的方程没有实数根;(2)求函数的单调区间;(3)设数列{xn}满足,当a=2且,证明:对任意m∈N*...