本试题 “物体以初速度v0作竖直上抛运动,上升过程可以看成是两种简单直线运动的合成,合速度用vy表示,以y为正方向,重力加速度g已知,下列说法正确的是( )A.vy比...” 主要考查您对竖直上抛运动
力的合成
力的分解
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 竖直上抛运动
- 力的合成
- 力的分解
竖直上抛运动:
将物体以一定初速度沿竖直方向向上抛出,物体只在重力作用下运动(不考虑空气阻力作用),叫做竖直上抛运动。
竖直上抛运动的公式:
vt=v0-gt;h=v0t-![]() gt2;速度位移公式:vt2-v02=-2gh。
gt2;速度位移公式:vt2-v02=-2gh。
运动特征:
①运动到最高点v=0,a=-g(取竖直向下方向为正方向);
②能上升的最大高度hmax=![]() ;
;
③质点在通过同一高度位置时,上升速度与下落速度大小相等;物体在通过一段高度过程中,上升时间与下落时间相等,![]() 。
。
④物体只受重力作用,具有竖直向上的初速度。
运动性质:
初速度不为零的匀变速直线运动。
竖直上抛的处理方法:
1、分段处理法:
①上升阶段:已知v0,a=-g,vt=0的匀减速直线运动,取向上为正方向较方便。所以运动规律为
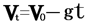 ,
, ,
,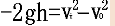
故,上升时间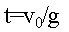 ,最大高度
,最大高度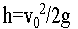 。
。
②最高点v=0,可是不处于静止状态,因为a=g。
③下降阶段:自由落体运动,取向下为正方向较方便。
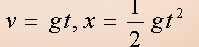
2、对称性:
①竖直上抛的物体上抛达到最大高度与从这一高度落回抛出点所用的时间相等。
②竖直上抛物体在上升和下落过程中经过同一位置时的速度大小相等方向相反。
3、V-t图像:
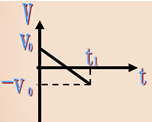
4、整体分析法:
将全过程看成是加速度为-g的匀变速直线运动,应用公式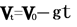 ,
,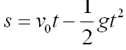
(1)s为正,表示质点在抛出点的上方,s为负表示在抛出点的下方。
(2)由同一s求出的t、可能有两个解,要注意分清其意义。
(3)算出的vt>0表示物体在向上过程中,vt<0表示物体在向下过程中;s>0表示物体在抛出点上方,s<0表示物体在抛出点下方.
当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的效果跟原来几个力的共同效果相同,这个力就叫做那几个力的合力,原来的几个力叫做这个力的分力。
①合力与分力是针对同一受力物体而言的。
②一个力之所以是其他几个力的合力,或者其他几个力之所以是这个力的分力,是冈为这一个力的作用效果与其他几个力共同作用的效果相当,合力与分力之间的关系是一种等效替代的关系。
③合力可能大于任何一个分力,也可能小于任何一个分力,也可能介于两个分力之间。
④如果两个分力的大小不变,夹角越大,合力就越小;夹角越小,合力就越大。
⑤两个大小一定的力F1、F2,其合力的大小范围
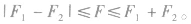

力的运算法则:
1.平行四边形定则
作用在同一点的两个互成角度的力的合力,不等于两分力的代数和,而是遵循平行四边形定则。如果以表示两个共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用这两个邻边之间的对角线表示,这叫做力的平行四边形定则,如图所示。 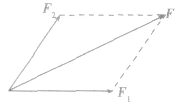
2.三角形定则和多边形定则如图(a)所示,两力F1、F2合成为F的平行四边形定则,可演变为(b)图,我们将(b)图称为三角形定则合成图,即将两分力F1、F2首尾相接,则F就是由F,的尾端指向F2的首端的有向线段所表示的力。
如果是多个力合成,则由三角形定则合成推广可得到多边形定则,如图为三个力F1,F2、F3的合成图,F 为其合力。
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
力的分解的几种情况:
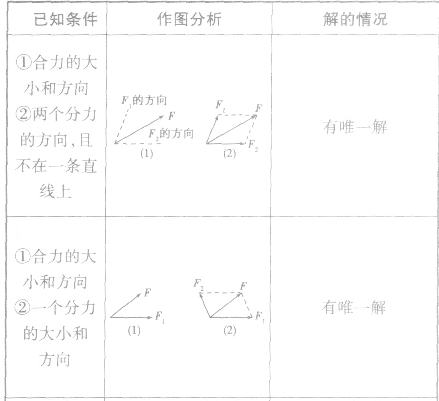
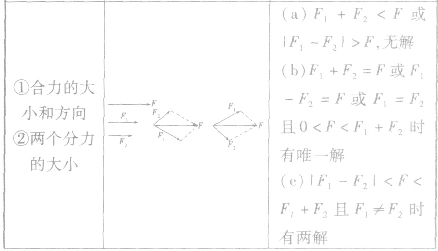
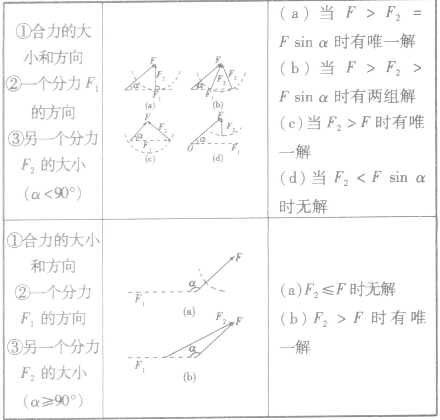
分解方法:
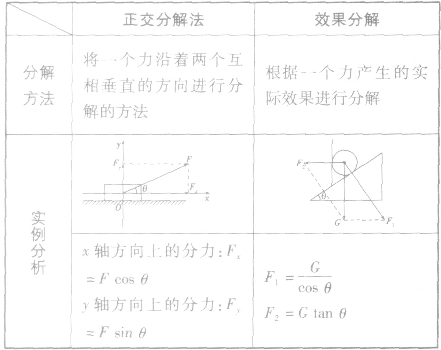
几种按效果分解的实例:


由力的三角形定则求力的最小值:
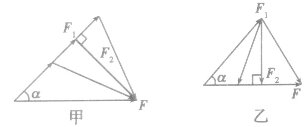
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值
 。
。 (2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值
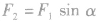 。
。
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值
 。
。由圆的切线求力方向的极值:
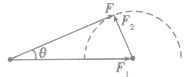
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足
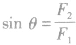 。
。 
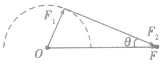
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足
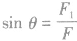 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足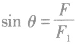 。
。
与“物体以初速度v0作竖直上抛运动,上升过程可以看成是两种简单...”考查相似的试题有:
- A球自距地面高h处开始自由下落,同时B球以初速度v0正对A球竖直上抛,空气阻力不计。问:(1)要使两球在B球上升过程中相遇,...
- 下图能正确反映竖直上抛运动速度、加速度、位移和动能随时间变化关系的是( )(以向上为正方向,以抛出点开始记时,位移起点...
- 一个物体在水平地面上由静止开始在水平力F的作用下前进了距离s,然后撤去F,物体又前进了距离2s停下来,那么,物体在运动中受...
- 如图所示,某同学在地面上拉着一个质量为m=30kg的箱子匀速前进,已知箱与地面间的动摩擦因数为μ=0.5,拉力F1与水平面夹角为θ=...
- (附加题)2008年春节前后,我国南方大部分省区遭遇了罕见的雪灾,此次灾害过程造成17个省(区、市、兵团)不同程度受灾.尤...
- L型木板P(上表面光滑)放在固定斜面上,轻质弹簧一端固定在木板上,另一端与置于木板上表面的滑块Q相连,如图所示.若P、Q一...
- 如图所示.木块A、B的质量分别是mA=5.0kg和mB=6.0kg,它们与水平地面之间的动摩擦因数均为μ=0.2,一轻弹簧原长为l0=10cm、劝...
- (1)在做“验证力的平行四边形定则”实验时,橡皮条的一端固定在木板上,用两个弹簧秤把橡皮条的另一端拉到某一确定的O点,则...
- 已知两个大小相等的共点力作用在同一物体上,当它们之间的夹角为120°时,其合力大小为6N。若其它条件不变,只改变这两个力之...
- 如图所示,质量为m的物体在沿斜面向上的拉力F作用下,沿放在水平地面上的质量为M的粗糙斜面匀速上滑,斜面倾角为θ,此过程中...