本试题 “轻质细线吊着一质量为m=0.32 kg,边长为L=0.8 m、匝数n=10的正方形线圈,总电阻为r=1 Ω。边长为的正方形磁场区域对称分布在线圈下边的两侧,如图甲所示,磁场...” 主要考查您对电功率
法拉第电磁感应定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 电功率
- 法拉第电磁感应定律
电功率:
1、定义:单位时间内电流做的功叫电功率
2、公式:P=W/t=UI,这是计算电功率普遍适用的公式,![]() 只适用于纯电阻电路。
只适用于纯电阻电路。
3、单位:瓦(W),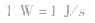
4、物理意义:电流做功的快慢
5、适用条件:任何电路
6、能量转化情况:单位时间内消耗电能的多少
电动机的三个功率及关系:

用电器额定功率和实际功率:
(1)用电器正常工作时所加的电压叫做额定电压,在额定电压下消耗的功率是额定功率,即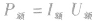 。当用电器两端电压达到额定电压
。当用电器两端电压达到额定电压 时,电流达到额定电流
时,电流达到额定电流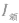 ,电功率也达到额定功率
,电功率也达到额定功率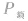 ,对于纯电阻用电器,
,对于纯电阻用电器,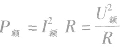 。
。
(2)实际功率是指用电器在实际电压下消耗的功率,即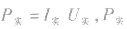 不一定等于
不一定等于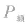 。若
。若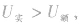 ,则
,则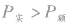 ,用电器可能被烧坏;若
,用电器可能被烧坏;若 ,则
,则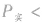
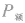 。实际功率不能长时间超过额定功率。
。实际功率不能长时间超过额定功率。
法拉第电磁感应定律:
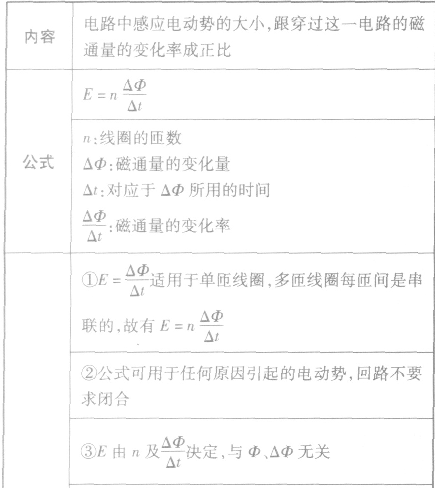

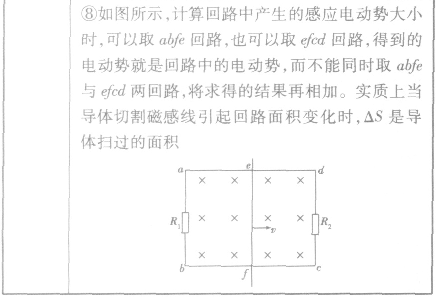
导体切割磁感线的两个特例:

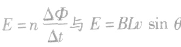 的区别与联系及选用原则:
的区别与联系及选用原则: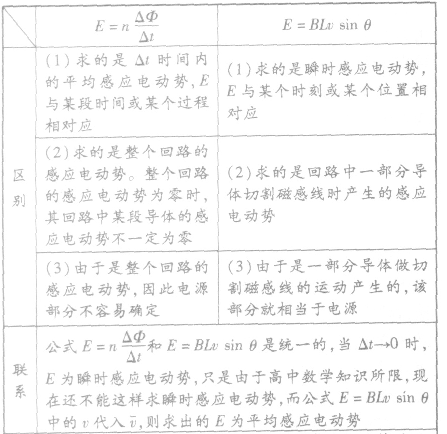

电磁感应中动力学问题的解法:
电磁感应和力学问题的综合,其联系的桥梁是磁场对感应电流的安培力,因为感应电流与导体运动的加速度有相互制约的关系。
1.分析思路
(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向。
(2)求回路中的电流。
(3)分析研究导体受力情况(包含安培力,用左手定则确定其方向)。
(4)列动力学方程或平衡方程求解。
2.常见的动态分析这类问题中的导体一般不是做匀变速运动,而是经历一个动态变化过程再趋于一个稳定状态,故解这类问题时正确进行动态分析确定最终状态是解题的关键。同时也要抓好受力情况和运动情况的动态分析,研究顺序为:导体受力运动产生感应电动势一感应电流一通电导体受安培力一合外力变化一加速度变化一速度变化一周而复始地循环,循环结束时,加速度等于零.导体达到稳定运动状态。
电磁感应中的动力学临界问题:
(1)解决这类问题的关键是通过运动状态的分析,寻找过程中的临界状态,如速度、加速度求最大值或最小值的条件。
(2)基本思路: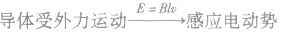
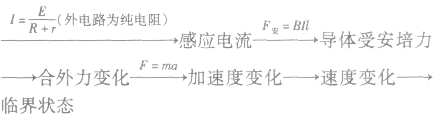
与“轻质细线吊着一质量为m=0.32 kg,边长为L=0.8 m、匝数n=10的...”考查相似的试题有:
- 某一用直流电动机提升重物的装置,重物的质量m=50kg,电源电压为120V.当电动机以v=0.9m/s的恒定速度向上提升重物时,电路中...
- 如图所示电路中,R1为定值电阻,R2为可变电阻,E为电源电动势,r为电源内阻.则以下说法中正确的是( )A.当R2=R1+r时,R2上...
- 有一铜块,重量为G,密度为D,电阻率为ρ.把它拉制成截面半径为r的导线,再用它做成一半径为R的圆形回路(R>>r).现加一个...
- 闭合回路的磁通量φ随时间t变化的图象分别如图①-④所示,关于回路中产生的感应电动势的下列论述,其中正确的是( )A.图①回路...
- 如图所示,固定于水平绝缘面上的平行金属导轨不光滑,垂直于导轨平面有一匀强磁场.质量为m的金属棒cd垂直放在导轨上,除R和cd...
- 如图5所示,匀强磁场方向垂直纸面向里,导体棒AB在金属框上向右运动;以下说法正确的是:A.AB中无电流B.AB中有电流,方向由...
- 如图示,两块水平放置的金属板间距为d,用导线与一个匝数为n的截面积为S的线圈相连,线圈总电阻为r,线圈中有竖直向上的磁场...
- 法拉第电磁感应定律可以这样表述:闭合电路中感应电动势的大小[ ]A.跟穿过这一闭合电路的磁通量成正比B.跟穿过这一闭合电路...
- 关于电路中感应电动势的大小,下列说法正确的是[ ]A.穿过电路的磁通量越大,感应电动势就越大B.电路中磁通量的改变量越大,...
- 某种小发电机的内部结构平面图如图1所示,永久磁体的内侧为半圆柱面形状,它与共轴的圆柱形铁芯间的缝隙中存在辐向分布、大小...