返回

高中二年级物理

首页
首页 高中二年级物理知识 碰撞 氢原子的能级 试题正文
  • 计算题
    (1)氢原子第n能级的能量为，其中E1是基态能量，而n=1，2……若一氢原子发射能量为的光子后处于比基态能量高出的激发态，则氢原子发射光子前后分别处于第几能级？
    (2)一速度为v的高速α粒子与同方向运动的氖核发生弹性正碰，碰后α粒子恰好静止。求碰撞前后氖核的速度。（不计相对论修正）
    本题信息：2011年同步题物理计算题难度极难 来源:马凤霞
  • 本题答案
    查看答案
本试题 “(1)氢原子第n能级的能量为，其中E1是基态能量，而n=1，2……若一氢原子发射能量为的光子后处于比基态能量高出的激发态，则氢原子发射光子前后分别处于第几能级...” 主要考查您对

碰撞

氢原子的能级

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 碰撞
  • 氢原子的能级
碰撞：

1、特点：
①时间：过程持续时间即相互作用时间极短
②作用力：在相互作用的过程中，相互作用力先是急剧增大，然后再急剧减小，平均作用力很大
③动量守恒条件：系统的内力远远大于外力，所以，系统即使所受外力之和不为零，外力也可以忽略，系统的总动量守恒
④位移：碰撞过程是在一瞬间发生的，时间极短，所以，在物体发生碰撞的瞬间，可忽略物体的位移，可以认为物体在碰撞前后仍在同一位置
⑤能量：在碰撞过程中，一般伴随着机械能的损失，碰撞后系统的总动能要小于或等于碰撞前系统的总动能，
2、两物体相碰通常有以下三种情况
①两物体碰撞后，动能无损失，称为弹性碰撞。当两相等质量的物体发生弹性碰撞时，则发生速度交换，这是一个很有用的结论。
 
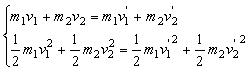
②两物体碰撞后虽分开，但动能有损失，称为非弹性碰撞。
 
③两物体碰撞后合为一个整体，以某一共同速度运动，称为完全非弹性碰撞。此类碰撞中动能损失最多，即动能转化为其他形式能的值最多。

弹性碰撞及讨论:

质量为m1与质量为m2的物体分别以速度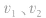运动并发生对心碰撞，碰撞过程中无机械能损失(如图所示)。

设碰后两物体的速度分别为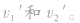
据动量守恒得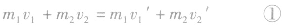
据机械能守恒得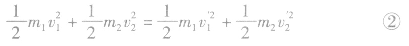
由①②两式得
由上述表达式可以看出：
(1)若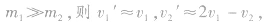
(2)若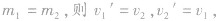即速度交换。
(3)若，即m2的速度几乎不变。

“一动一静”模型:

(1)弹性正碰，如图所示，在光滑水平面上质量为 m1的小球以速度v1与质量为m2的静止小球发生弹性正碰．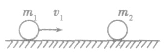

讨论碰后两球的速度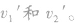根据动量守恒和机械能守恒有：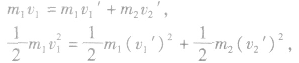

解上面两式可得：
碰后m1的速度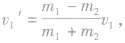
碰后m2的速度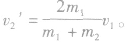
讨论：
①若表示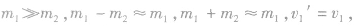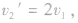表示m1的速度不变，m2以2v1速度被撞出去。
②若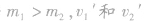都是正值，表示都与v1方向相同。
③若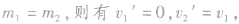，则有即碰后两球速度互换。
④若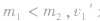为负值，表示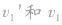方向相反， m1被弹回。
⑤若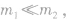这时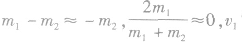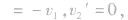表示m1被反向以原速率弹回，而m2仍静止。
⑥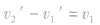
两物体碰后的速度随两物体的质量比变化情况如图所示。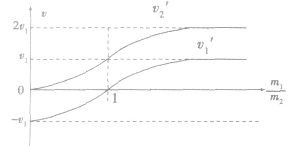

⑦能量传递：在弹性碰撞中，传递的能量跟两者质量比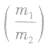有关，即两球质量越接近，碰撞中传递的动能越大；在两种情况下，传递的动能相等。
(2)完全非弹性碰撞上例中m1与m2发生完全非弹性碰撞，则有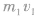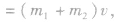，碰后的共同速度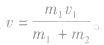
损失的动能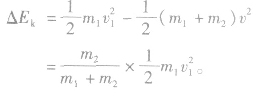

 “二合一”模型:

这种模型是指两个速度不同的物体通过发生相互作用，最终两物体粘在一起运动或以共同的速度运动的模型。
这种模型的主要特征是终态共速(也可以是只在某一时刻共速．而研究的过程是从初始到共速的过程)，从能量角度来看，这种过程中能量损失是最大的，属于完全非弹性碰撞的类型，在一维碰撞中的方程有：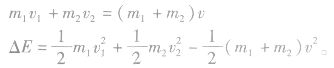

相互作用的两个物体在很多情况下皆可当成碰撞处理，那么对相互作用中两物体相距“恰最近”、相距 “恰最远”或“恰上升到最高点”等一类，临界问题，求解的关键都是“速度相等”。在“类碰撞”问题中，碰撞时间不一定很短,但遵守的规律却是相同的，例如下面几种情形。
(1)如图中，光滑水平面上的A物体以速度v0去撞击静止的B物体，A、B两物体相距最近时,两物体速度必定相等，此时弹簧最短，其压缩量最大，系统损失的动能等于弹簧获得的弹性势能，

(2)在图中，物体A以速度v0滑到静止在光滑水平面上的小车B上，当A在B上滑行的距离最远时，A、B相对静止，A、B的速度必定相等，系统损失的动能等于AB间摩擦产生的热量。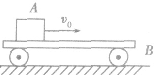

(3)在图中，子弹以速度v0射入静止在光滑的水平面上的木块中。当子弹不穿出时，子弹和木块的速度必定相等，系统损失的动能等于子弹与木块间摩擦产生的热量。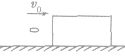

(4)如图所示，质量为M的滑块静止在光滑水平面上，滑块的光滑弧面底部与桌面相切，一个质量为m 的小球以速度v0向滑块滚来。设小球不能越过滑块，则小球到达滑块上的最高点时(即小球在竖直方向上的速度为零)，两者的速度肯定相等(方向为水平向右)，小球获得的重力势能等于系统损失的动能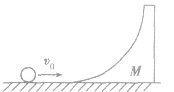

碰撞合理性的判断方法:

碰撞的合理性要遵循动量守恒定律、能量关系和速度关系：
1．系统动量守恒
 
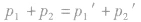
2．碰撞过程中系统的总动能不会增加
如果物体发生的是弹性碰撞，总动能不变；其他情况碰撞后会有部分动能转化为内能，系统的动能将减小。即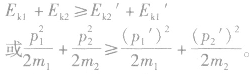

3．速度要符合情景如果碰前两物体同向运动，则后面物体的速度必大于前面物体的速度，即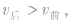否则无法实现碰撞。碰撞后，原来在前的物体速度一定增大，且原来在前的物体速度大于或等于原来在后的物体速度，即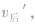否则碰撞没有结束。如果碰前两物体是相向运动，则碰后，两物体的运动方向不可能都不改变，除非两物体碰撞后速度均为零。


氢原子的能级:

1、氢原子的能级图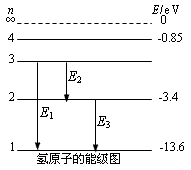

2、光子的发射和吸收
①原子处于基态时最稳定，处于较高能级时会自发地向低能级跃迁，经过一次或几次跃迁到达基态，跃迁时以光子的形式放出能量。
②原子在始末两个能级Em和En（m>n）间跃迁时发射光子的频率为ν，其大小可由下式决定：hυ=Em-En。
③如果原子吸收一定频率的光子，原子得到能量后则从低能级向高能级跃迁。
④原子处于第n能级时，可能观测到的不同波长种类N为：。
⑤原子的能量包括电子的动能和电势能（电势能为电子和原子共有）即：原子的能量En=EKn+EPn。轨道越低，电子的动能越大，但势能更小，原子的能量变小。
电子的动能：，r越小，EK越大。


氢原子的能级及相关物理量:

在氢原子中，电子围绕原子核运动，如将电子的运动看做轨道半径为r的圆周运动，则原子核与电子之间的库仑力提供电子做匀速圆周运动所需的向心力，那么由库仑定律和牛顿第二定律，有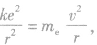，则
①电子运动速率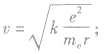
②电子的动能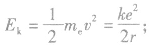
③电子运动周期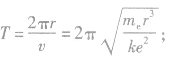
④电子在半径为r的轨道上所具有的电势能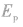
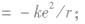
⑤等效电流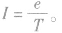由以上各式可见，电子绕核运动的轨道半径越大，电子的运行速率越小，动能越小，电子运动的周期越大．在各轨道上具有的电视能越大。

原子跃迁时光谱线条数的确定方法:

1．直接跃迁与间接跃迁
原子从一种能量状态跃迁到另一种能量状态时，有时可能是直接跃迁，有时可能是间接跃迁，两种情况辐射(或吸收)光子的频率可能不同。
2．一群原子和一个原子
氧原子核外只有一个电子，这个电子在某个时刻只能处在某一个可能的轨道上，在某段时间内，由某一轨道跃迁到另一个轨道时，可能的情况只有一种，但是如果容器中盛有大量的氢原子，这些原子的核外电子跃迁时就会有各种情况出现了。
3．一群氢原子处于量子数为n的激发态时，可能辐射的光谱线条数
如果氢原子处于高能级，对应量子数为n，则就有可能向量子数为(n一1)，(n一2)，(n一3)…1诸能级跃迁，共可形成(n一1)条谱线，而跃迁至量子数为(n一 1)的氢原子又可向(n一2)，(n一3)…1诸能级跃迁，共可形成(n一2)条谱线。同理，还可以形成(n一3)，(n 一4)…1条谱线。将以上分析结果归纳求和，则从量子数为n对应的能级向低能级(n—1)，(n一2)…1跃迁可形成的谱线总条数为(n一1)+(n一2)+(n一3)+ …+1=n(n一1)／2。数学表示为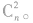
4．一个氢原子处于量子数为n的激发态时，可能辐射的光谱线条数
对于处于量子数为n的一个氢原子，它可能发生直接跃迁，只放出一个光子，也可能先跃迁到某个中间能级上，再跃迁回基态而放出两个光子，也可能逐级跃迁，即先跃迁到n一1能级上，再跃迁到n一2能级上， ……，最后回到基态上，共放出n—1个光子。即一个氢原子在发生能级跃迁时，最少放出一个光子，最多可放出n一1个光子。

利用能量守恒及氢原子能级特征解决跃迁电离等问题的方法:

在原子的跃迁及电离等过程中，总能量仍是守恒的。原子被激发时，原子的始末能级差值等于所吸收的能量，即入射光子的全部能量或者入射粒子的全部或部分能量；原子被电离时，电离能等于原子被电离前所处能级的绝对值，原子所吸收的能量等于原子电离能与电离后电离出的电子的动能之和；辐射时辐射出的光子的能量等于原子的始末能级差。氢原子的能级 F 关系为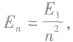，第n能级与量子数n2成反比，导致相邻两能级间的能量差不相等，量子数n越大，相邻能级差越小，且第n能级与第n一1能级的差比第n能级与无穷远处的能级差大，即另外，能级差的大小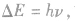故也可利用光子能量来判定能级差大小。


跃迁与电离:

激发的方式:


发现相似题
与“(1)氢原子第n能级的能量为，其中E1是基态能量，而n=1，2……若...”考查相似的试题有：