本试题 “如图所示,滑块质量为m,受一大小为3mRg水平冲量后,沿动摩擦因数为0.1的水平地面滑行5R,并冲上一半径为R的光滑14圆弧,在圆弧边沿正上方R高处有一旋转圆形...” 主要考查您对线速度
角速度
动能定理
动量
冲量
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 线速度
- 角速度
- 动能定理
- 动量
- 冲量
线速度的定义:
质点沿圆周运动通过的弧长与所用时间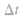 的比值叫做线速度。
的比值叫做线速度。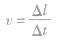 ,
,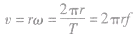 。
。
线速度的特性:
线速度是矢量,方向和半径垂直,和圆周相切。它是描述做圆周运动的物理运动快慢的物理量。
对线速度的理解:
物体上任一点对定轴作圆周运动时的速度称为“线速度”。它的一般定义是质点作曲线运动时所具有的顺时速度。它的方向沿运动轨道的切线方向,故又称切向速度。它是描述作曲线运动的质点运动快慢和方向的物理量。物体上各点作曲线运动时所具有的顺时速度,其方向沿运动轨道的切线方向。 (高中物理中的切线方向就指速度一侧的方向,和数学中的切线不同)
知识点拨:
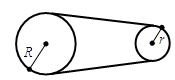
如图,大圆和小圆有同一根皮带相连,皮带上的各个点的速率相同,所以大圆和小圆圆周上的线速度是相同的。
角速度的定义:
圆周运动中,连接质点和圆心的半径转过的角度 跟所用时间
跟所用时间 的比值叫做角速度。
的比值叫做角速度。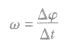 ,
,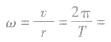
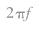 。
。
角速度的特性:
角速度是矢量,高中阶段不研究其方向。它是描述做圆周运动的物体绕圆心转动快慢的物理量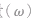 。
。
单位:在国际单位制中,单位是“弧度/秒”(rad/s)。(1rad=360d°/(2π)≈57°17'45″)
转动周数时(例如:每分钟转动周数),则以转速来描述转动速度快慢。角速度的方向垂直于转动平面,可通过右手螺旋定则来确定。(角速度的方向,在高中物理的学习不属于考察的内容)
线速度和角速度的对比:
角速度是单位时间转过的角度;或者说是转过的角度和所用时间的比值。
线速度是单位时间走过的弧长;或者说是弧长和所用时间的比值。
角速度和线速度的关系:
知识拓展提升:
例:计算地球和月亮公转的角速度:

通过计算知道,书中所提到的地球和月球的争论是没有结论的。比较运动得快慢,要看比较线速度还是角速度,不能简单说谁快谁慢。
动能定理:
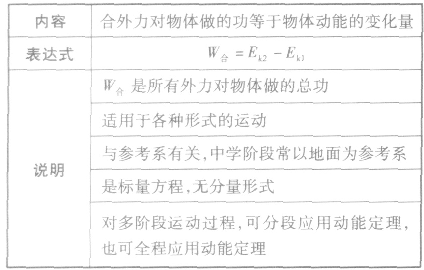
动能定理的应用方法技巧:
1.应用动能定理解题的基本思路
(1)选取研究对象,明确并分析运动过程。
(2)分析受力及各力做功的情况,求出总功:
(3)明确过程始、末状态的动能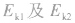 。
。
(4)列方程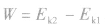 ,必要时注意分析题目潜在的条件,列辅助方程进行求解。
,必要时注意分析题目潜在的条件,列辅助方程进行求解。
2.应用动能定理应注意的几个问题
(1)明确研究对象和研究过程,找出始末状态的速度。
(2)要对物体正确地进行受力分析,明确各力做功的大小及正负情况(待求的功除外)。
(3)有些力在物体运动过程中不是始终存在的。若物体运动过程中包括几个阶段,物体在不同阶段内的受力情况不同,在考虑外力做功时需根据情况区分对待。
3.几种应用动能定理的典型情景
(1)应用动能定理求路程在多阶段或往返运动中,如果摩擦力或介质阻力大小不变,方向与速度方向关系恒相反,则在整个过程中克服摩擦力或介质阻力所做的功等于力与路程的乘积,从而可将物体在摩擦力或介质阻力作用下通过的路程与动能定理联系起来。
(2)应用动能定理求解多过程问题物体在某个运动过程中包含几个运动性质不同的小过程(如加速、减速的过程),此时可以分段考虑,也可以对全过程考虑,但如能对整个过程根据动能定理列式求解,则可以使问题简化。根据题意灵活地选取研究过程,可以使问题变得简单。有时取全过程简单,有时取某一阶段简单。原则是尽量使做功的力减少,各个力的功计算方便,或使初、未动能等于零。
(3)用动能定理求变力的功变力的功无法用公式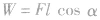 直接求解,有时该力也不是均匀变化的,无法用高中知识表达平均力,此时可以考虑用动能定理间接求解。涉及功、能的极值问题在涉及功、能的极值问题中,有些极值的形成是南运动形式的临界状态造成的。如竖直平面内圆周运动的最高点、平抛运动等。有些极值的形成是由题设条件造成的。在解决涉及功、能的极值问题时,一种思路是分析运动形式的临界状态,将临界条件转化为物理方程来求解;另一种思路是将运动过程的方程解析式化,利用数学方法求极值。
直接求解,有时该力也不是均匀变化的,无法用高中知识表达平均力,此时可以考虑用动能定理间接求解。涉及功、能的极值问题在涉及功、能的极值问题中,有些极值的形成是南运动形式的临界状态造成的。如竖直平面内圆周运动的最高点、平抛运动等。有些极值的形成是由题设条件造成的。在解决涉及功、能的极值问题时,一种思路是分析运动形式的临界状态,将临界条件转化为物理方程来求解;另一种思路是将运动过程的方程解析式化,利用数学方法求极值。
知识拓展:
1.总功的计算物体受到多个外力作用时,计算合外力的功,一般有如下三种方法:
(1)先由力的合成与分解法或根据牛顿第二定律求出合力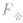 ,然后由
,然后由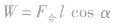 计算。采用此法计算合力的总功时,一是要求各力同时作用在物体上。二是要求合外力是恒力。
计算。采用此法计算合力的总功时,一是要求各力同时作用在物体上。二是要求合外力是恒力。
(2)由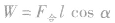 计算各个力对物体做的功
计算各个力对物体做的功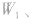
 ,然后将各个外力所做的功求代数和。当多阶段运动过程中不同阶段物体所受外力不同,即外力分阶段作用在物体上时常用此法求外力的总功。
,然后将各个外力所做的功求代数和。当多阶段运动过程中不同阶段物体所受外力不同,即外力分阶段作用在物体上时常用此法求外力的总功。
(3)外力做的总功等于物体动能的变化量,在物体初、末状态已知的情况下可考虑从动能变化量来确定合外力做的功。
2.系统动能定理
动能定理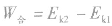 实质上是一个质点的功能关系,是针对单体或可看做单个物体的物体系而言的。所谓能看成单个物体的物体系,简单来说就是物体系内各物体之间的相对位置不变,从而物体系的各内力做功之和为零.物体系的动能变化就取决于所有外力做的总功了。
实质上是一个质点的功能关系,是针对单体或可看做单个物体的物体系而言的。所谓能看成单个物体的物体系,简单来说就是物体系内各物体之间的相对位置不变,从而物体系的各内力做功之和为零.物体系的动能变化就取决于所有外力做的总功了。
但是对于不能看成单个物体的物体系或不能看成质点的物体,可将其看成是由大量质点组成的质点系,对质点系组成的系统应用动能定理时,就不能仅考虑外力的作用,还需考虑内力所做的功。即: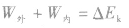
如人在从地面上竖直跳起的过程中,只受到了重力、地面支持力两个力的作用,而人从下蹲状态到离开地面的过程中,支持力不对人做功,重力对人做负功,但人的动能增加了,原因就在于此过程中人不能被看成单一的质点,人体内肌肉、骨骼之间的内力对人也做功。再如光滑水平面上由静止释放两带异种电荷的小球,对两小球组成的系统来说,没有外力对它们做功,但它们的动能却增加了,原因也在于它们的内力对它们做了功。
3.动能、动能的变化与动能定理的比较: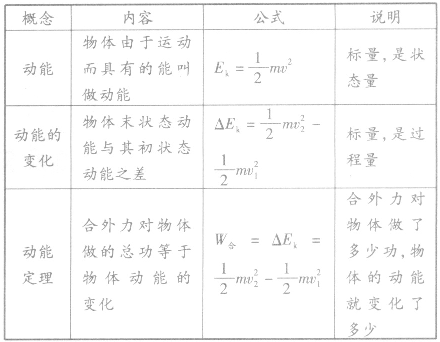
动量:
1.定义:物体的质量(m)跟其速度(v)的乘积(mv)叫做物体的动量,用符号p表示
2.定义式:p=mv
3.单位:千克·米/秒,符号kg·m/s
4.标矢性:矢量,方向与速度同向
5.状态量:对应于某一时刻或某一位置
6.相对性:与参考系有关,通常取地面为参考系
7.引入意义:①为了描述力作用一段时间后对物体产生的效果。②为了揭示相互作用的物体系统,在作用过程中遵守的规律
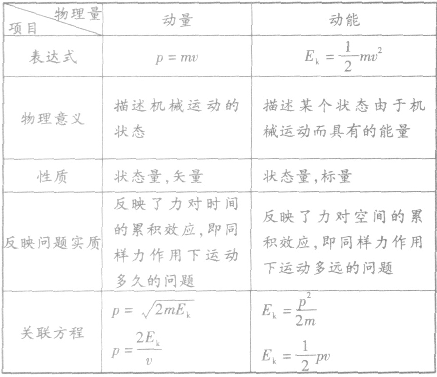
动量与动能:
冲量:
定义
力与力的作用时间的乘积叫力的冲量
定义式
I=Ft
标失性
力是矢量,冲量也是矢量
过程性
冲量是描述力对物体作用的时间积累效应的物理量,力越大,作用时间越长,冲量就越大
绝对性
由于力和时间都跟参考系的选择无关,因此冲量也跟参考系的选择无关;另外物体受某个力的冲量只取决于这个力及其作用时间,与物体的运动状态、是否受其他力无关
单位
牛顿·秒,简称牛·秒,符号N·s
备注
(1)冲量表达式,I=Ft只适用于计算恒力的冲量;计算变力的冲量一般用动量定理。
(2)如图所示,在力F随时间t变化的F—t图像中,图线与时间轴之间的“面积”为力的冲量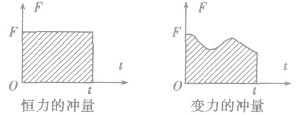
(3)合外力冲量的计算。
①如果物体受到的各个力作用的时间相同,且都为恒力,可用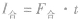 计算;
计算;
②如果在物体运动的整个过程中不同阶段受力不同,则合冲量为各个阶段冲量的矢量和
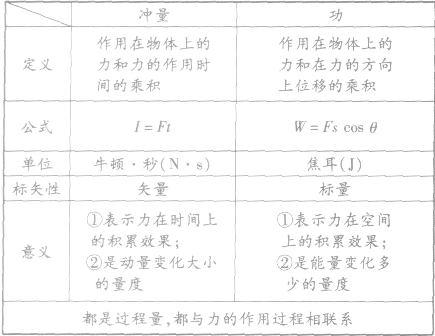
冲量和功的区别:
与“如图所示,滑块质量为m,受一大小为3mRg水平冲量后,沿动摩擦...”考查相似的试题有:
- 不定项选择细绳的一端捆着一块小石头作匀速圆周运动,当小石头绕转至图(一)中的P点时,细绳突然断裂,则图(二)中表示细线断裂...
- 毛泽东主席著名诗句,“坐地日行八万里,巡天遥看一千河”,这里的“一里”为0.5km.(1)试说明“坐地日行八万里”的科学道理.(2)人在...
- 在赤道的物体A和在杭州的物体B随地球自转而做匀速圆周运动,如图所示,它们的线速度分别为vA、vB,周期分别为TA、TB,则( )...
- 如图所示,固定斜面的倾角θ=30°,物体A与斜面之间的动摩擦因数为,轻弹簧下端固定在斜面底端,弹簧处于原长时上端位于C点....
- 一质量为2 kg的物体被人用手提着由静止开始提升了1.5 m,物体的速度是2 m/s,在此过程中,合力做的功为__________J;物体克服...
- 将质量为m的重球与较长的细丝线组成单摆,小振幅振动(摆角小于5°)时周期为T。使小球带电量为q的正电后,置于水平向右的匀强...
- 如图所示,水平轨道AB与位于竖直面内半径为R的半圆形光滑轨道BCD相连,半圆形轨道的直径BD与AB垂直,水平轨道上有一质量m=1.0...
- (10分)如图所示,有一倾角为θ=370的硬杆,其上套一底端固定且劲度系数为k=120N/m的轻弹簧,弹簧与杆间无摩擦。一个质量为m...
- 如图甲所示, A、B、C、D为固定于竖直平面内的闭合绝缘轨道,AB段、CD段均为半径R=1.6 m的半圆,BC、AD段水平,AD=BC=8 m...
- 下列说法正确的是( )A.合外力对质点做的功为零,则质点的动能、动量都一定不改变B.合外力对质点施的冲量不为零,则质点的...