本试题 “1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽...” 主要考查您对动能定理
质谱仪
回旋加速器
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 动能定理
- 质谱仪
- 回旋加速器
动能定理:
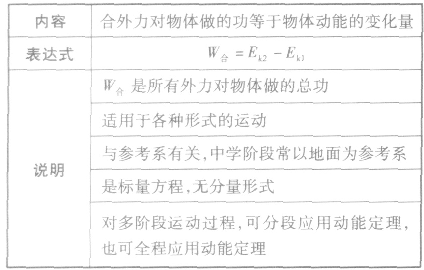
动能定理的应用方法技巧:
1.应用动能定理解题的基本思路
(1)选取研究对象,明确并分析运动过程。
(2)分析受力及各力做功的情况,求出总功:
(3)明确过程始、末状态的动能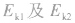 。
。
(4)列方程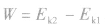 ,必要时注意分析题目潜在的条件,列辅助方程进行求解。
,必要时注意分析题目潜在的条件,列辅助方程进行求解。
2.应用动能定理应注意的几个问题
(1)明确研究对象和研究过程,找出始末状态的速度。
(2)要对物体正确地进行受力分析,明确各力做功的大小及正负情况(待求的功除外)。
(3)有些力在物体运动过程中不是始终存在的。若物体运动过程中包括几个阶段,物体在不同阶段内的受力情况不同,在考虑外力做功时需根据情况区分对待。
3.几种应用动能定理的典型情景
(1)应用动能定理求路程在多阶段或往返运动中,如果摩擦力或介质阻力大小不变,方向与速度方向关系恒相反,则在整个过程中克服摩擦力或介质阻力所做的功等于力与路程的乘积,从而可将物体在摩擦力或介质阻力作用下通过的路程与动能定理联系起来。
(2)应用动能定理求解多过程问题物体在某个运动过程中包含几个运动性质不同的小过程(如加速、减速的过程),此时可以分段考虑,也可以对全过程考虑,但如能对整个过程根据动能定理列式求解,则可以使问题简化。根据题意灵活地选取研究过程,可以使问题变得简单。有时取全过程简单,有时取某一阶段简单。原则是尽量使做功的力减少,各个力的功计算方便,或使初、未动能等于零。
(3)用动能定理求变力的功变力的功无法用公式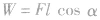 直接求解,有时该力也不是均匀变化的,无法用高中知识表达平均力,此时可以考虑用动能定理间接求解。涉及功、能的极值问题在涉及功、能的极值问题中,有些极值的形成是南运动形式的临界状态造成的。如竖直平面内圆周运动的最高点、平抛运动等。有些极值的形成是由题设条件造成的。在解决涉及功、能的极值问题时,一种思路是分析运动形式的临界状态,将临界条件转化为物理方程来求解;另一种思路是将运动过程的方程解析式化,利用数学方法求极值。
直接求解,有时该力也不是均匀变化的,无法用高中知识表达平均力,此时可以考虑用动能定理间接求解。涉及功、能的极值问题在涉及功、能的极值问题中,有些极值的形成是南运动形式的临界状态造成的。如竖直平面内圆周运动的最高点、平抛运动等。有些极值的形成是由题设条件造成的。在解决涉及功、能的极值问题时,一种思路是分析运动形式的临界状态,将临界条件转化为物理方程来求解;另一种思路是将运动过程的方程解析式化,利用数学方法求极值。
知识拓展:
1.总功的计算物体受到多个外力作用时,计算合外力的功,一般有如下三种方法:
(1)先由力的合成与分解法或根据牛顿第二定律求出合力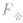 ,然后由
,然后由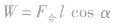 计算。采用此法计算合力的总功时,一是要求各力同时作用在物体上。二是要求合外力是恒力。
计算。采用此法计算合力的总功时,一是要求各力同时作用在物体上。二是要求合外力是恒力。
(2)由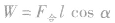 计算各个力对物体做的功
计算各个力对物体做的功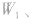
 ,然后将各个外力所做的功求代数和。当多阶段运动过程中不同阶段物体所受外力不同,即外力分阶段作用在物体上时常用此法求外力的总功。
,然后将各个外力所做的功求代数和。当多阶段运动过程中不同阶段物体所受外力不同,即外力分阶段作用在物体上时常用此法求外力的总功。
(3)外力做的总功等于物体动能的变化量,在物体初、末状态已知的情况下可考虑从动能变化量来确定合外力做的功。
2.系统动能定理
动能定理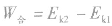 实质上是一个质点的功能关系,是针对单体或可看做单个物体的物体系而言的。所谓能看成单个物体的物体系,简单来说就是物体系内各物体之间的相对位置不变,从而物体系的各内力做功之和为零.物体系的动能变化就取决于所有外力做的总功了。
实质上是一个质点的功能关系,是针对单体或可看做单个物体的物体系而言的。所谓能看成单个物体的物体系,简单来说就是物体系内各物体之间的相对位置不变,从而物体系的各内力做功之和为零.物体系的动能变化就取决于所有外力做的总功了。
但是对于不能看成单个物体的物体系或不能看成质点的物体,可将其看成是由大量质点组成的质点系,对质点系组成的系统应用动能定理时,就不能仅考虑外力的作用,还需考虑内力所做的功。即: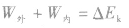
如人在从地面上竖直跳起的过程中,只受到了重力、地面支持力两个力的作用,而人从下蹲状态到离开地面的过程中,支持力不对人做功,重力对人做负功,但人的动能增加了,原因就在于此过程中人不能被看成单一的质点,人体内肌肉、骨骼之间的内力对人也做功。再如光滑水平面上由静止释放两带异种电荷的小球,对两小球组成的系统来说,没有外力对它们做功,但它们的动能却增加了,原因也在于它们的内力对它们做了功。
3.动能、动能的变化与动能定理的比较: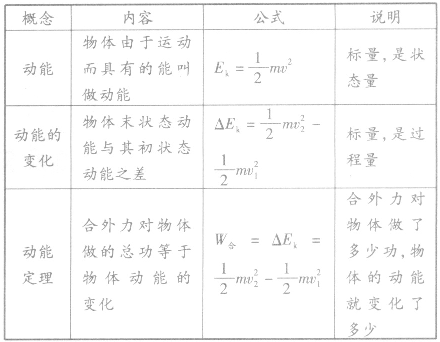
质谱仪:
具有相同核电荷数而不同质量数的原子互称同位素,质谱仪是分离各种元素的同位素并测量它们质量的仪器,它由静电加速器、速度选择器、偏转磁场、显示屏等组成,它的结构原理如图所示。 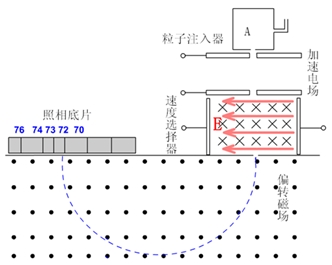
如图所示,离子源S产生质量为m,电荷量为q的正离子(所受重力不计)。离子出来时速度很小(可忽略不计),经过电压为U的电场加速后进入磁感应强度为B的匀强磁场中做匀速圆周运动,经过半个周期到达记录它的照相底片P上,测得它在P上的位置到入口处的距离为L,则 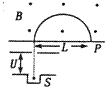
![]()
联立求解得![]() 。
。
因此,只要知道q、B、L与U,就可计算出带电粒子的质量m。
速度选择器:
(1)平行板中电场强度E和磁感应强度B互相垂直,这种装置能把具有一定速度的粒子选择出来,所以叫做速度选择器,如图所示。
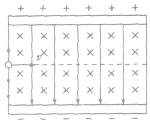
(2)带电粒子能够沿直线匀速通过速度选择器的条件是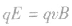 ,即
,即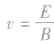 ,与带电粒子的质量,所带电荷的正负、电荷量均无关,只与速度有关。
,与带电粒子的质量,所带电荷的正负、电荷量均无关,只与速度有关。
(3)若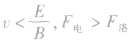 ,粒子向电场力方向偏,电场力做正功,粒子动能增加;
,粒子向电场力方向偏,电场力做正功,粒子动能增加;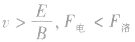 ,粒子向磁场力方向偏,电场力做负功,动能减少。
,粒子向磁场力方向偏,电场力做负功,动能减少。
回旋加速器:
(1)构造:
回旋加速器的核心部件是两个D 形扁金属盒,整个装置放在真空容器中,如图所示。 
①两个D形盒之间留有一个窄缝,在中心位置放有粒子源。
②两个D形盒分别接在高频交变电源的两极上,在两盒间的窄缝中形成一个方向呈周期性变化的交变电场。
(2)原理:
利用电场对带电粒子的加速作用和磁场对运动电荷的偏转作用来获得高能粒子,如图所示。 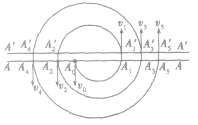
①磁场的作用:带电粒子以某一速度垂直于磁场方向进入匀强磁场时,只在洛伦兹力作用下做匀速圆周运动,其中周期与速度和半径无关,使带电粒子每次进入D形盒中都能运动相等时间(半个周期)后,平行于电场方向进入电场中加速。
②交流电压:为了保证每次带电粒子经过狭缝时均被加速,使能量不断提高,要在狭缝处加一个周期与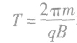 相同的交流电压。
相同的交流电压。
(3)特点
①带电粒子在D形盒中的回转周期等于两盒狭缝间高频电场的变化周期,与带电粒子速度无关(磁场保证带电粒子做回旋运动,如图所示)。
②带电粒子在D形金属盒内运动的轨道半径不等距分布。设带正电粒子的质量为m,电荷量为q,狭缝间加速电压大小为U,粒子源产生的带电粒子,经电场加速第一次进入左半盒时速度和半径分别为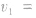
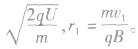 。
。
第二次进入左半盒时,经电场加速3次,进人左半盒的速度和半径为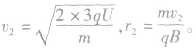
第k次进入左半盒时,经电场加速(2k一1)次,进入左半盒时速度和半径为
所以,任意相邻两轨道半径之比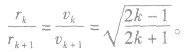
可见带电粒子在D形金属盒内运动时,越靠近D 形金属盒的边缘,相邻两轨道的间距越小。
③带电粒子在回旋加速器内运动的最终能量。由于D形金属盒的大小一定,所以不管粒子的大小及带电荷量如何,粒子最终从加速器内射出时应具有相同的旋转半径。
由牛顿第二定律得
动量大小与动能之间存在定量关系
由①②两式得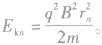
可见,带电粒子离开回旋加速器的动能与加速电压无关,而仅受磁感应强度B和D形盒半径的限制。加速电压的大小只能影响带电粒子在D形盒内加速的次数。
④带电粒子在回旋加速器内的运动时间。带电粒子在回旋加速器内运动时间的长短,与带电粒子做匀速圆周运动的周期有关,同时还与带电粒子在磁场中转动的圈数有关。设带电粒子在磁场中转动的圈数为n,加速电压为U。因每加速一次粒子获得的能量为qU,每圈有两次加速。结合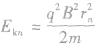 知
知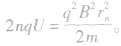 因此:
因此:
所以带电粒子在回旋加速器内运动时间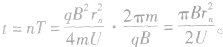
⑤由于随着带电粒子速度的增大,当速度接近光速时,据爱因斯坦狭义相对论可知,粒子质量增大,回转周期变大,而与交变电压周期不一致,使加速器无法正常工作,所以回旋加速器不能无限地对带电粒子加速。
与“1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工...”考查相似的试题有:
- 如图所示,绝缘水平面上的AB区域宽度为d,带正电、电量为q、质量为m的小滑块以大小为v0的初速度从A点进入AB区域,当滑块运动...
- 物体以60焦的初动能从A点出发做竖直上抛,在它上升到某一高度时,动能减少了30焦,而机械能损失了10焦.若物体在运动过程中所...
- 如图,一质量为m=10kg的物体,由1/4光滑圆弧轨道上端从静止开始下滑,到达底端后沿水平面向右滑动1m距离后停止。已知轨道半径...
- 质量mA=3.0kg、长度L=0.60m、电量q=4.0×10-5C的导体板A在绝缘水平面上,质量mB=1.0kg可视为质点的绝缘物块B在导体板A上的左端...
- 如图所示,利用动滑轮来吊起质量为20kg的物体,已知拉力F=140N,滑轮与绳的质量以及摩擦均不计,则当物体由静止开始升高1m时...
- “神舟”六号载人航天飞船的返回舱,在接近地面时打开降落伞后继续下落,下落速度仍达v="8" m/s.为了实现软着陆,在返回舱离地面约...
- 如图所示,质量为m的物体(可视为质点)以水平速度v0滑上原来静止在光滑水平面上、质量为M的小车上,物体与小车表面间的动摩...
- 如图所示,MPQ为竖直面内一固定轨道,MP是半径为R的1/4光滑圆弧轨道,它与水平轨道PQ相切于P,Q端固定一竖直挡板,PQ长为s....
- 如图所示的平行板器件中.电场强度E和磁感应强度B相互垂直,具有不同水平速度的带电粒子从P孔射入后发生偏转的情况不同.利用...
- 回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D形金属盒.两盒间的狭缝中形成的周期性变化的...