本试题 “下列说法正确的是( )A.由ρ=mV可知,ρ与m成正比与V成反比.B.由V=st可知,匀速运动时,V与S成正比C.由P=ρgh可知,压强与密度和高度有关D.由p=Wt可知,在...” 主要考查您对液体压强的计算
功率的计算
密度公式的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 液体压强的计算
- 功率的计算
- 密度公式的应用
P=ρgh(ρ是液体密度,单位是千克/米3;g=9.8牛/千克;h是深度,指液体自由液面到液体内部某点的竖直距离,单位是米。)
对液体压强公式 的理解
的理解
1.由公式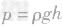 可知,液体内部的压强只跟液体的密度和深度有关,而跟液体的质量、重力、体积以及容器的形状、底面积等无关。
可知,液体内部的压强只跟液体的密度和深度有关,而跟液体的质量、重力、体积以及容器的形状、底面积等无关。
2.公式只适用于计算静止的液体产生的压强,而对固体、气体或流动的液体均不适用。
3.在液体压强公式中h表示深度,而不是高度。判断出h的大小是计算液体压强的关键,如图所示,甲图中A点的深度为30cm,乙图中B点的深度为 40cm.丙图中C点的深度为50cm。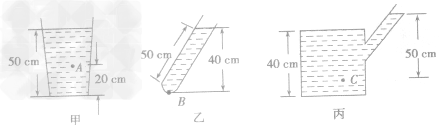
4.运用公式时应统一单位:ρ的单位用kg/m3,h 的单位用m,计算出的压强单位才是Pa。
5.两公式的区别与联系: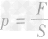 是压强的定义式, 无论固体、液体还是气体,它都是普遍适用的;而
是压强的定义式, 无论固体、液体还是气体,它都是普遍适用的;而 是结合液体的具体情况通过
是结合液体的具体情况通过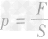 推导出来的,所以适用于液体。
推导出来的,所以适用于液体。
6.用公式求出的压强是液体由于自身重力产生的压强,它不包括液体受到的外加压强。
转换法和控制变量法探究液体压强大小跟哪些因素有关:
在探究液体压强的大小时,由于液体压强的大小不易测量或是不能直接观测到它的大小,我们用“转换法”,通过液体压强计中两玻璃管液面的高度差的大小来比较液体压强的大小,将抽象的东西变成了直观且形象的东两,使问题简化了。
由于液体内部压强跟液体的深度和液体密度两方面因素有关,所以在探究液体内部压强的规律时要采用控制变量法,即在探究液体压强与深度的关系时,要保持液体密度不变,在探究液体压强与液体的密度关系时,要保持液体的深度不变。
(1)P=W/t,其中P代表功率,单位为W,W代表功,单位为J;t代表时间,单位为s。
(2)因为P=W/t,W=Fs,v=s/t,所以P=W/t=Fs/t=Fv,P=Fv是功率的又一表达式。
公式法计算功率:
运用 时一定要注意三个量的对应关系。“W”一定是对应“t”完成的,不能张冠李戴。单位要统一,P、W、t的单位分别为瓦、焦、秒。
时一定要注意三个量的对应关系。“W”一定是对应“t”完成的,不能张冠李戴。单位要统一,P、W、t的单位分别为瓦、焦、秒。
例1 如图所示,铁明同学向上跳台阶进行晨练,铁明重500N,在10s内匀速连跳12个台阶,每个台阶的高度为0.2m。在这个过程中,已知铁明克服摩擦做功为2800J,求出此过程中: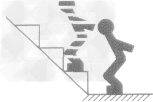
(1)铁明竖直向上跳的平均速率多大?
(2)铁明克服重力做功是多少?
(3)铁明做功的总功率多大?
解析:竖直向上跳的平均速度可以通过向上跳的总高度与所用时间利用速度公式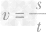 求出,克服重力做功等于重力与高度的乘积,即
求出,克服重力做功等于重力与高度的乘积,即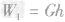 ,总功率可以通过所做的总功和时间利用功率公式
,总功率可以通过所做的总功和时间利用功率公式 求得。
求得。
(1)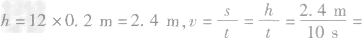 0.24m/s
0.24m/s
(2)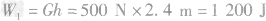
(3)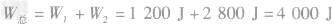
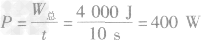
例2在打捞海底沉船时,常用水下机器人潜入水下打捞船上物品,已知ρ海水=1.03×103kg/m3。
(1)机器人在水下70m处受到海水产生的压强是多大?
(2)某时刻机器人在水下用竖直向上的力举着体积为0.02m3,密度为2.7×103kg/m3的物体静止不动,求该力的大小。
(3)若机器人在水下运动时,所受海水阻力与速度的关系如图所示,求机器人在水下以0.5m/s的水平速度匀速运动时,机器人水平推进力的功率。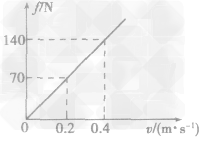
解析:(1)由液体压强公式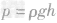 得,
得,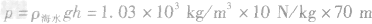 ,
,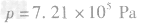
(2)物体在水下受平衡力的作用,则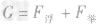
则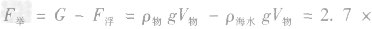
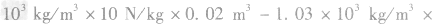

(3)由题图可知,海水阻力与机器人的运动速度成正比,当机器人运动速度为0.5m/s时,f=175N 机器人匀速前进时,机器人水平推进力F=f
P=Fv=175N×0.5m/s=87.5W
答案:(1)7.21×105Pa(2)334N(3)87.5W
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比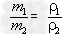 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比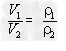 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
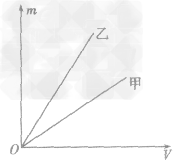
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
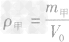 ,ρ乙=
,ρ乙= 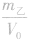 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。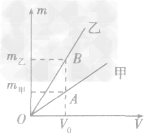
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,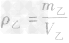
(2)写出该物理量比的表达式:
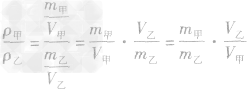
(3)化简:代入已知比值的求解:
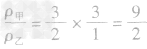
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
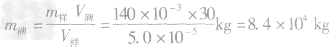 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
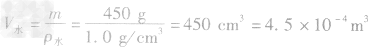 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为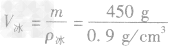 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,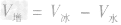 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
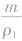 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=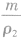 ,合金的体积
,合金的体积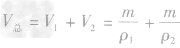 ,则合金的密度
,则合金的密度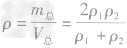
在(2)中两种金属的体积相等,设为
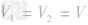 ,合金的体积
,合金的体积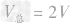 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=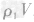 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为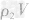 ,合金的质量m总
,合金的质量m总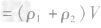 ,合金的密度为
,合金的密度为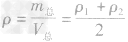 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
与“下列说法正确的是( )A.由ρ=mV可知,ρ与m成正比与V成反比....”考查相似的试题有:
- 一个杯子中盛满水,把一个小木块放入杯中时,木块浮在水面上.此时杯底受到的水的压强将______,压力将______.(选填“变大”...
- 中山舰是“浓缩了中国现代史”的一代名舰,其排水量780t,长64.48m,宽8.99m,它在安全航行中受到的最大浮力为________N。1938...
- 用压强计“探究影响液体内部压强大小的因素”;①图中所示压强计是通过U形管中液面的______________来反映被测压强大小的.使用...
- 重500N的物体A在50N的拉力F作用下以0.2m/s的速度匀速移动,如图所示,则3s内拉力做的功是__________J,拉力的功率是________...
- 甲、乙两个同学的体重相同,各自从1楼上到5楼,若甲是走上去的而乙是跑着上去的,则( )A.甲做的功多,但功率较小B.乙做的...
- 如图所示,工人利用动滑轮在10 s内将重为100N的重物(包括桶)沿竖直方向匀速向上提升了5m。若该动滑轮重10N,忽略绳与滑轮之...
- 在多哈亚运会中,一举重运动员在2.5s内用1000N的力把杠铃举高了2m,在这段时间内,他做功的功率为 ______W;如果他举起杠铃后...
- 把一金属块浸没在盛满酒精的杯中,从杯中溢出10g酒精,若将该金属块浸没在盛满水的杯中,则从杯中溢出的水的质量[ ]A.大于10...
- 由同种不锈钢制成的饭锅、饭盒、小勺,根据公式ρ=m/V,可以得出的结论是( )A.锅的质量大,所以饭锅的密度大B.饭盒的体积...
- 一瓶铭牌标有5L(1L=10-3m3)d的“鲁花”牌花生油,密度为0.94×103㎏/m3,质量为______㎏.这瓶花生油用去一半后,剩下花生油的...