本试题 “质量m=1.0kg的甲物体与竖直放置的轻弹簧的上端连接,弹簧下端固定在地面上,如右图所示.质量m=1.0kg的乙物体从甲物体正上方,距离甲物体h=0.40m处自由落下,...” 主要考查您对自由落体运动
机械能守恒定律
动量守恒定律
简谐运动的振幅
简谐运动的周期、频率和角频率
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 自由落体运动
- 机械能守恒定律
- 动量守恒定律
- 简谐运动的振幅
- 简谐运动的周期、频率和角频率
自由落体运动:
物体只在重力作用下从静止开始下落的运动叫做自由落体运动。
自由落体运动的公式:
v=gt;h=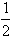 gt2;v2=2gh。
gt2;v2=2gh。
运动性质:
自由落体运动是初速度为零的匀加速直线运动。
自由落体加速度:
在同一地点,一切物体在自由落体运动中的加速度都相同,这个加速度叫自由落体加速度,也叫重力加速度。
物体做自由落体运动的条件:
①只受重力而不受其他任何力,包括空气阻力。
②从静止开始下落。
重力加速度g:
①方向:总是竖直向下的。
②大小:g=9.8m/s2,粗略计算可取g=10m/s2
③在地球上不同的地方,g的大小不同.g随纬度的增加而增大(赤道g最小,两极g最大),g随高度的增加而减小。
知识点拨:
自由落体运动的规律:
自由落体运动是初速度为零的匀加速直线运动,所以,匀变速直线运动公式也适用于自由落体运动。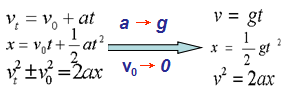
小知识--重力加速度:
①把地球当做旋转椭球,重力加速度计算公式为:g=9.7803(1+0.0052884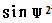 -0.0000059
-0.0000059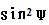 2)m/s2
2)m/s2
式中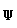 为物体所在处的地理纬度
为物体所在处的地理纬度
②重力加速度还和物体离地面的高度h有关。当h远小于地球半径R时,
小知识—空气阻力:
空气阻力是物体在空气中运动时受到的阻力。空气阻力的大小与物体相对于空气的速度、物体的形状等都有很大的关系。
1、内容:只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变。
2、表达式:
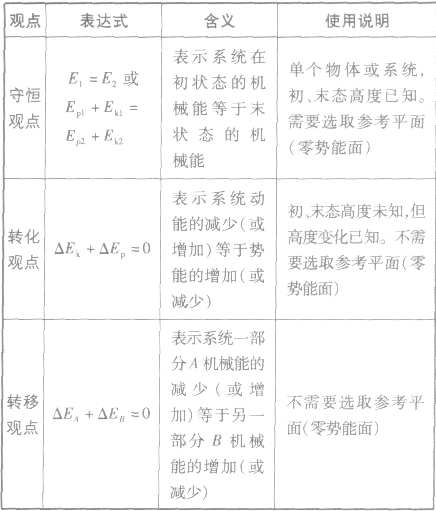
3.条件
机械能守恒的条件是:只有重力或弹力做功。可以从以下三个方面理解:
(1)只受重力作用,例如在不考虑空气阻力的情况下的各种抛体运动,物体的机械能守恒。
(2)受其他力,但其他力不做功,只有重力或弹力做功。例如物体沿光滑的曲面下滑,受重力、曲面的支持力的作用,但曲面的支持力不做功,物体的机械能守恒。
(3)其他力做功,但做功的代数和为零。
判定机械能守恒的方法:
(1)条件分析法:应用系统机械能守恒的条件进行分析。分析物体或系统的受力情况(包括内力和外力),明确各力做功的情况,若对物体或系统只有重力 (或弹力)做功,没有其他力做功或其他力做功的代数和为零,则系统的机械能守恒。
(2)能量转化分析法:从能量转化的角度进行分析:若只有系统内物体间动能和重力势能及弹性势能的相互转化,系统跟外界没有发生机械能的传递,机械能也没有转化成其他形式的能(如内能),则系统的机械能守恒。
(3)增减情况分析法:直接从机械能的各种形式的能量的增减情况进行分析。若系统的动能与势能均增加或均减少,则系统的机械能不守恒;若系统的动能不变,而势能发生了变化,或系统的势能不变,而动能发生了变化,则系统的机械能不守恒;若系统内各个物体的机械能均增加或均减少,则系统的机械能不守恒。
(4)对一些绳子突然绷紧、物体间非弹性碰撞等,除非题目特别说明,否则机械能必定不守恒。
竖直平面内圆周运动与机械能守恒问题的解法:
在自然界中,违背能量守恒的过程肯定是不能够发生的,而不违背能量守恒的过程也不一定能够发生,因为一个过程的进行要受到多种因素的制约,能量守恒只是这个过程发生的一个必要条件。如在竖直平面内的变速圆周运动模型中,无支撑物的情况下,物体要到达圆周的最高点,从能量角度来看,要求物体在最低点动能不小于最高点与最低点的重力势能差值。但只满足此条件物体并不一定能沿圆弧轨道运动到圆弧最高点。因为在沿圆弧轨道运动时还需满足动力学条件:所需向心力不小于重力,由此可以推知,在物体从圆弧轨道最低点开始运动时,若在动能全部转化为重力势能时所能上升的高度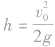 满足
满足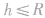 时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在
时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在 ,物体上升到圆周最高点时的速度
,物体上升到圆周最高点时的速度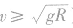 )时,物体可做完整的圆周运动;若在
)时,物体可做完整的圆周运动;若在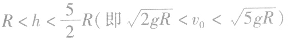 时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度
时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度 满足
满足 。故在解决这类问题时不能单从能量守恒的角度来考虑。
。故在解决这类问题时不能单从能量守恒的角度来考虑。
1、内容:一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变。
2、表达式:m1v1+m2v2=m1v1'+m2v2'。
3、动量守恒定律成立的条件:
①系统不受外力或系统所受外力的合力为零;
②系统所受的外力的合力虽不为零,但系统外力比内力小得多,如碰撞问题中的摩擦力,爆炸过程中的重力等外力比起相互作用的内力来小得多,可以忽略不计;
③系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变。
4、动量守恒的速度具有“四性”:
①矢量性;②瞬时性;③相对性;④普适性。
动量守恒定律与机械能守恒定律的比较:



系统动量守恒的判断方法:
方法一:南动量守恒的条件判断动量守恒的步骤如下:
(1)明确系统由哪几部分组成。
(2)对系统中各物体进行受力分析,分清哪些是内力,哪些是外力。
(3)看所有外力的合力是否为零,或内力是否远大于外力,从而判断系统的动量是否守恒。
方法二:南系统动量变化情况判断动量守恒方法如下:
(1)明确初始状态系统的总动量是多少。
(2)对系统内的物体进行受力分析、运动分析,确定每一个物体的动量变化情况。
(3)确定系统动量变化情况,进而判定系统的动量是否守恒。
振动物体离开平衡位置的最大距离,是标量,表示振动的强弱。
周期T和频率f:
1.意义:表示振动快慢的物理量,周期越短,频率越高,振动越快
2.定义:
完成一次全振动所需要的时间,用T表示
单位时间内完成全振动的次数,用f表示
3.关系:Tf=1
4.决定因素:周期与频率由振动系统本身决定,与振幅无关
5.角频率ω:ω=2πf。
应用简谐运动的对称性及周期性的解题方法:
如图所示, 物体在A与B间运动,O点为平衡位置,C和D两点关于O点对称,则有:
物体在A与B间运动,O点为平衡位置,C和D两点关于O点对称,则有:
1.时间的对称性 
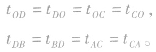
2.速度的对称性
(1)物体连续两次经过同一点(如D点)的速度大小相等,方向相反。
(2)物体经过关于D点对称的两点(如C与D两点)的速度大小相等,方向可能相同,也可能相反。
3.周期性简谐运动是一种周而复始的周期性的运动,按其周期性可作如下判断:
(1)若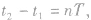 则
则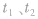 两时刻振动物体在同一位置,运动情况相同。
两时刻振动物体在同一位置,运动情况相同。
(2)若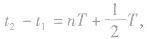 则
则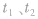 两时刻,描述运动的物理量
两时刻,描述运动的物理量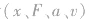 均大小相等,方向相反。
均大小相等,方向相反。
(3)若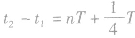 或
或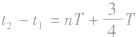 ,则当
,则当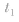 时刻物体在最大位移处时,
时刻物体在最大位移处时,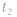 时刻物体到达平衡位置;当t1时刻物体在平衡位置时,t2时刻物体到达最大位移处;若t1时刻物体在其他位置,t2时刻物体到达何处就要视具体情况而定。
时刻物体到达平衡位置;当t1时刻物体在平衡位置时,t2时刻物体到达最大位移处;若t1时刻物体在其他位置,t2时刻物体到达何处就要视具体情况而定。
与“质量m=1.0kg的甲物体与竖直放置的轻弹簧的上端连接,弹簧下端...”考查相似的试题有:
- 关于自由落体运动,下列说法正确的是( )A.物体竖直向下的运动就是自由落体运动B.加速度等于重力加速度的运动就是自由落体...
- 如图所示,小球Q在竖直平面内做匀速圆周运动,当Q球转到图示位置时,有另一小球P在距圆周最高点为h处开始自由下落,要使两球...
- 如图所示,小球P被悬挂在距地面高为H处,一水平放置的枪指向小球射击,枪口A与小球P等高,距离为S,如果在开枪射击时小球同时...
- 某人在同一地点从同一高度同时释放质量不等的甲、乙两个物体,且m甲>m乙.则在下落过程中( )A.甲的重力加速度大于乙物体...
- 如图所示,质量为M的“∟”形物体,固定在水平面上,物体的AB部分是半径为R的四分之一光滑圆弧,BC部分是粗糙水平面,将质量为m...
- 下列与能量有关的说法正确的是( )A.卫星绕地球做圆周运动的半径越大,动能越小B.在只有静电力做功时,系统机械能守恒C....
- (9分) 如图,质量为m的小船甲在静止在水面上,一质量为m/3的人站在船尾。另一相同小船乙以速率v0从后方驶来,为避免两船相...
- 如图所示,A、B两个木块质量分别为2kg与0.9kg,A、B与水平地面间接触光滑,上表面粗糙,质量为0.1kg的铁块以10m/s的速度从A的...
- 如图所示,、两物体的质量之比,原来静止在平板小车上,、间有一根被压缩的弹簧,地面光滑。当弹簧突然释放后,、两物体被反...
- 如图所示,在光滑水平面上有两辆车处于静止状态,其上分别站有甲、乙两个小孩,每辆车和小孩的总质量均为M,甲车上的小孩拿着...