本试题 “如图所示,水平抛出的物体,抵达斜面上端P处时速度恰好沿着斜面方向,紧贴斜面PQ无摩擦滑下;ABCD为物体沿x方向和y方向运动的位移-时间图象及速度-时间图象,...” 主要考查您对平抛运动
从受力确定运动情况
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 平抛运动
- 从受力确定运动情况
平抛运动的定义:
将物体以一定的初速度沿水平方向抛出,不考虑空气阻力,物体只在重力作用下所做的运动,叫做平抛运动。
平抛运动的特性:
以抛出点为坐标原点,水平初速度V0,竖直向下的方向为y轴正方向,建立如图所示的坐标系,在该坐标系下,对任一时刻t: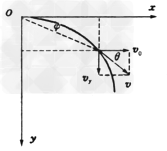
①位移
分位移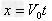 (水平方向),
(水平方向),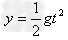 (竖直方向);
(竖直方向);
合位移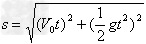 ,
, (φ为合位移与x轴夹角)。
(φ为合位移与x轴夹角)。
②速度
分速度 (水平方向),Vy=gt(竖直方向);
(水平方向),Vy=gt(竖直方向);
合速度 ,
,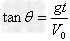 (θ为合速度V与x轴夹角)。
(θ为合速度V与x轴夹角)。
③平抛运动时间: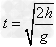 (取决于竖直下落的高度)。
(取决于竖直下落的高度)。
④水平射程: (取决于竖直下落的高度和初速度)。
(取决于竖直下落的高度和初速度)。
类平抛运动:
(1)定义当物体所受的合外力恒定且与初速度垂直时,物体做类平抛运动。
(2)类平抛运动的分解方法
①常规分解法:将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力的方向)的匀加速直线运动,两分运动彼此独立,互不影响,且与合运动具有等时性。
②特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为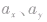 ,,初速度
,,初速度 分解为
分解为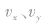 ,然后分别在x、y方向上列方程求解。
,然后分别在x、y方向上列方程求解。
(3)类平抛运动问题的求解思路
根据物体受力特点和运动特点判断该问题属于类平抛运动问题——求出物体运动的加速度——根据具体问题选择用常规分解法还是特殊分解法求解。
(4)类抛体运动
当物体在巨力作用下运动时,若物体的初速度不为零且与外力不在一条直线上,物体所做的运动就是类抛体运动。
在类抛体运动中可采用正交分解法处理问题,基本思路为:
①建立直角坐标系,将外力、初速度沿这两个方向分解。
②求出这两个方向上的加速度、初速度。
③确定这两个方向上的分运动性质,选择合适的方程求解。
从受力确定运动情况:
1、知道物体受到的全部作用力,应用牛顿第二定律求加速度,再应用运动学公式求出物体的运动情况。
2、分析这两点问题的关键是抓住受力情况和运动情况的桥梁——加速度。
3、由物体的受力情况求解物体的运动情况的一般方法和步骤:
①确定研究对象,对研究对象进行受力分析,并画出物体的受力图;
②根据力的合成与分解的方法,求出物体所受的合外力(包括大小和方向);
③根据牛顿第二定律列方程,求出物体的加速度;
④结合给定的物体运动的初始条件,选择运动学公式,求出所需的运动参量,并分析讨论结果是否正确合理。
动力学中临界、极值问题的解决方法:
(1)在运用牛顿运动定律解决动力学有关问题时,常常会讨论相互作用的物体是否会发生相对滑动,相互接触的物体是否会发生分离等,这类问题就是临界问题。临界问题是指物体的运动性质发生突变,要发生而尚未发生改变时的状态。此时运动物体的特殊条件往往是解题的突破口。本部分中常出现的临界条件为:
①绳子或杆的弹力为零;
②相对静止的物体间静摩擦力达到最大,通常在计算中取最大静摩擦力等于滑动摩擦力;
③接触面间弹力为零,但接触物体的速度、加速度仍相等。临界状态往往是极值出现的时刻,题目中常出现隐含临界状态的词语,如“最大”“最小”“最短”“恰好”等.
(2)解决临界问题的关键是要分析出临界状态,例如两物体刚好要发生相对滑动时,接触面上必出现最大静摩擦力,两个物体要发生分离时,相互之间的作用力——弹力必定为零。
(3)解决临界问题的一般方法
①极限法:题设中若出现“最大”“最小…‘刚好”等这类词语时,一般就隐含着临界问题,解决这类问题时,常常是把物理问题(或物理过程)引向极端,进而使临界条件或临界点暴露出来,达到快速解决有关问题的目的。
②假设法:有些物理问题在变化过程中可能会出现临界问题,也可能不出现临界问题,解答这类问题,一般要用假设法。
③数学推理法:根据分析的物理过程列出相应的数学表达式,然后由数学表达式讨论出临界条件。
变加速运动过程的分析方法:
力可以改变速度的大小,也可以改变速度的方向。在牛顿运动定律的应用中,常常会出现物体在变力作用下,对物体的运动情况作出定性判断。处理此类问题的关键是抓住力或加速度与速度之间的方向关系,即同向加速,反向减速,而至于加速度变大或变小,只是影响速度改变的快慢,如在分析自由下落的小球,下落一段时间与弹簧接触后的运动情况时,从它开始接触弹簧到弹簧被压缩到最短的过程中,加速度和速度的变化情况讨论如下(过程图示如图).
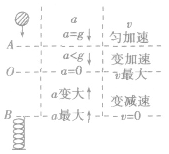
①小球接触弹簧上端后受两个力作用:向下的重力和向上的弹力,在接触后的前一阶段,重力大于弹力,合力向下,因为弹力F=kx不断增大,所以合力不断变小,故加速度也不断减小,由于加速度与速度同向,因此速度不断变大。
②当弹力逐渐增大到与重力大小相等时,合外力为零,加速度为零,速度达到最大。(注意:此位置是两个阶段的转折点)
③后一阶段,即小球到达上述平衡位置之后,由于惯性仍继续向下运动,但弹力大于重力,合力向上,且逐渐变大,因而加速度逐渐变大,方向向上,小球做减速运动,因此速度逐渐减小到零,到达最低点时,弹簧的压缩量最大。
与“如图所示,水平抛出的物体,抵达斜面上端P处时速度恰好沿着斜...”考查相似的试题有:
- 在一堵竖直高墙前S远处的高台上水平抛出A、B两小球,若两球抛出的初速度vA>vB,A、B两球分别打到高墙 a、b两点,则有( )A. ...
- 如图所示,圆桶底面半径为R,在上部有个入口A,在A的正下方h处有个出口B,在A处沿切线方向有一斜槽,一个小球恰能沿水平方向...
- 关于平抛运动,下列说法正确的是( )A:平抛运动是匀变速运动 B:平抛运动是变加速运动C:任意两段时间内加速度相同 D:任意...
- (14分)地面上有一个半径为R的圆形跑道,高为h的平台边缘上的P点在地面上P′点的正上方,P′与跑道圆心O的距离为L(L>R),如...
- 在同一平台上的O点抛出的3个物体,作平抛运动的轨迹如图所示,则3个物体作平抛运动的初速度vA,vB,vC的关系和3个物体平抛运...
- 如图所示,从高为h的斜面顶端A点以速度v0水平抛出一个小球,小球落在斜面底端B点(已知重力加速度大小为g,不计空气阻力),...
- 如图所示,水平台面AB距地面的高度h=0.80m.有一滑块从A点以v0=6.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩...
- 甲、乙两人在同一点O,分别向竖直墙壁MN水平投掷飞镖,落在墙上时,飞镖A与竖直墙壁夹角为α=53°,飞镖B与竖直墙壁夹角为β=37°...
- 如图,在距地面h高处以初速度v0沿水平抛出一个物体,不计空气阻力,物体在下落过程中,下列说法中正确的是( )A.物体在c点...
- 如图所示,一轻质弹簧一端系在墙上的O点,自由伸长到B点,今用一小物体m把弹簧压缩到A点,然后释放,小物体能运动到C点静止,...