本试题 “在水平地面上,有一小球A从某点以初速度v0=6m/s向右做匀加速直线运动.同时,在A球的正上方高h=20m处,另一小球B以速度vB=8m/s向右水平抛出,B球落地时刚好砸...” 主要考查您对匀变速直线运动的速度与时间的关系
匀变速直线运动的位移与时间的关系
平抛运动
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 匀变速直线运动的速度与时间的关系
- 匀变速直线运动的位移与时间的关系
- 平抛运动
匀变速直线运动:
物体在一条直线上运动,如果在相等的时间内速度的变化相等,这种运动就叫做匀变速直线运动。也可定义为:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动。
匀变速直线运动的速度公式:
Vt=V0+at。
公式说明:
- 速度公式是匀变速直线运动速度的一般表示形式。它所表明瞬时速度与时刻t的对应关系。
- 通常取初速度v0方向为正方向,加速度a可正可负(正、负表示方向),在匀变速直线运动中a恒定。
①当a与v0同方向时,a>0表明物体的速度随时间均匀增加,如下左图。
②当a与v0反方向时,a<0表明物体的速度随时间均匀减少,如下右图。
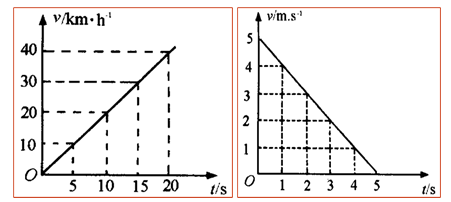
3. 速度图象是对速度公式的直观体现.图象斜率表示加速度,图象与时间轴所围的面积表示位移。
匀变速直线运动的位移公式:
由平均速度的定义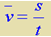 和匀变速直线运动的平均速度
和匀变速直线运动的平均速度 及速度公式
及速度公式 ,联立推导出匀变速直线运动的位移公式:
,联立推导出匀变速直线运动的位移公式: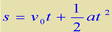
知识点拨:
1、是匀变速直线运动位移的一般表示形式.它能表明质点在各个时刻相对初始时刻(t=0)的位移。
2、在位移公式中s、v0、a均是矢量,解题时一般要选取v0方向为正。
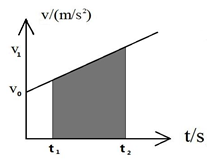
3、位移公式可由速度图象来推导,
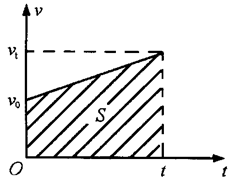
如图是某物体做匀变速直线运动的图象.根据图象的物理意义,它与横轴(时间轴)所围的那块梯形面积表示运动的位移.所以: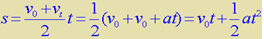
平抛运动的定义:
将物体以一定的初速度沿水平方向抛出,不考虑空气阻力,物体只在重力作用下所做的运动,叫做平抛运动。
平抛运动的特性:
以抛出点为坐标原点,水平初速度V0,竖直向下的方向为y轴正方向,建立如图所示的坐标系,在该坐标系下,对任一时刻t: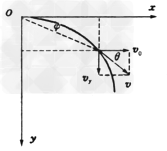
①位移
分位移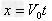 (水平方向),
(水平方向),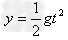 (竖直方向);
(竖直方向);
合位移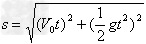 ,
, (φ为合位移与x轴夹角)。
(φ为合位移与x轴夹角)。
②速度
分速度 (水平方向),Vy=gt(竖直方向);
(水平方向),Vy=gt(竖直方向);
合速度 ,
,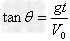 (θ为合速度V与x轴夹角)。
(θ为合速度V与x轴夹角)。
③平抛运动时间: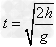 (取决于竖直下落的高度)。
(取决于竖直下落的高度)。
④水平射程: (取决于竖直下落的高度和初速度)。
(取决于竖直下落的高度和初速度)。
类平抛运动:
(1)定义当物体所受的合外力恒定且与初速度垂直时,物体做类平抛运动。
(2)类平抛运动的分解方法
①常规分解法:将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力的方向)的匀加速直线运动,两分运动彼此独立,互不影响,且与合运动具有等时性。
②特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为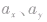 ,,初速度
,,初速度 分解为
分解为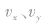 ,然后分别在x、y方向上列方程求解。
,然后分别在x、y方向上列方程求解。
(3)类平抛运动问题的求解思路
根据物体受力特点和运动特点判断该问题属于类平抛运动问题——求出物体运动的加速度——根据具体问题选择用常规分解法还是特殊分解法求解。
(4)类抛体运动
当物体在巨力作用下运动时,若物体的初速度不为零且与外力不在一条直线上,物体所做的运动就是类抛体运动。
在类抛体运动中可采用正交分解法处理问题,基本思路为:
①建立直角坐标系,将外力、初速度沿这两个方向分解。
②求出这两个方向上的加速度、初速度。
③确定这两个方向上的分运动性质,选择合适的方程求解。
与“在水平地面上,有一小球A从某点以初速度v0=6m/s向右做匀加速...”考查相似的试题有:
- 物体由静止开始运动,加速度恒定,在第7s内的初速度是2.6m/s,则物体的加速度是( )A.0.46m/s2B.0.37m/s2C.2.6m/s2D.0.4...
- 一物体以初速v0冲上斜面,斜面与物体问滑动摩擦系数为μ,到达最高点后又下滑,则在此过程中( )A.冲上过程的加速度比下滑时...
- 如图1所示,质量为60kg的消防队员从一根固定的竖直金属杆上由静止滑下,经过2.5s时间落到地面上.下滑中消防队员受到的竖直向...
- 海滨浴场的滑梯从顶端到入水处约12m,一个人由滑梯顶端开始做初速度为零的匀加速直线运动,开始运动1s后通过的位移是0.75m,...
- 一物体运动的位移与时间关系x=6t-4t2(x、t的单位分别为s、m)则( )A.这个物体的初速度为12m/sB.这个物体的初速度为6m/sC...
- (10分)汽车以1.6m/s的速度在水平地面上匀速行驶,汽车后壁货架上放有一小球(可视作质点),架高1.8 m。由于前方事故,突然...
- 有一个物体在高为h处,以初速度v0水平抛出,落地时的速度为vt,竖直分速度为vy,水平位移为S,则下列公式不能用来计算物体在...
- 中国计划在2017年实现返回式月球软着陆器对月球进行科学探测,宇航员在月球上着陆后,自高h处以初速度v0水平抛出一小球,测出...
- 如图,用小球在O点对准前方的一块竖直放置的挡板,O与A在同一高度。小球的水平初速度分别是ν1、ν2、ν3,不计空气阻力,打在挡...
- 在高为h的地方以初速v0平抛一物体,落地后水平位移为s,下列说法正确的是( )A 若将起抛点的高度升至2h,初速度不变,那么落...