本试题 “在衰变中常伴有一种称为“中微子”的例子放出。中微子的性质十分特别,因此在实验中很难探测。1953年,莱尼斯和柯文建造了一个由大水槽和探测器组成的实验系统...” 主要考查您对动量守恒定律的应用
粒子的波动性,德布罗意波
核反应
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 动量守恒定律的应用
- 粒子的波动性,德布罗意波
- 核反应
1、动量守恒定律:一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变。即m1v1+m2v2=m1v1'+m2v2'。
2、动量守恒定律的常见问题:
①碰撞问题;
②爆炸问题;
③反冲现象;
④人船模型;
“人船模型”是动量守恒定律的应用的一个经典模型,该模型应用的条件:一个原来处于静止状态的系统,当系统中的物体间发生相对运动的过程中,有一个方向上动量守恒。
⑤子弹打木块模型。
子弹打木块模型及推广:
Ⅰ、一物块在木板上滑动,μNS相对=ΔEk系统=Q,Q为摩擦在系统中产生的热量;
Ⅱ、小球在置于光滑水平面上的竖直平面内弧形光滑轨道上滑动,包括小车上悬一单摆单摆的摆动过程等。小球上升到最高点时系统有共同速度(或有共同的水平速度);系统内弹力做功时,不将机械能转化为其它形式的能,因此过程中系统机械能守恒。
Ⅲ、一静一动的同种电荷追碰运动等。
从“六性”把握动量守恒定律的应用方法:
1.条件性
动量守恒定律的成立是有条件的,只有当系统满足动量守恒的条件时才能利用方程式进行计算。
2.矢量性
动量守恒方程是一个矢量方程。对于作用前后物体的运动方向都在同一直线上的问题,应选取统一的正方向,凡是与选取正方向相同的动量为正,相反为负。若方向未知,可设为与正方向相同列动量守恒方程,通过解得结果的正负,判定未知量的方向。
3.参考系的同一性速度
具有相对性,公式中的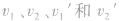 均应对同一参考系而言,一般均取对地的速度。
均应对同一参考系而言,一般均取对地的速度。
4.状态的同一性
相互作用前的总动量,这个“前”是指相互作用前的某一时刻,所以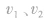 均是此时刻的瞬时速度,同理
均是此时刻的瞬时速度,同理 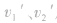 应是相互作用后的某一时刻的瞬时速度。
应是相互作用后的某一时刻的瞬时速度。
5.整体性
动量守恒定律是针对一个物体系统而言的,具有系统的整体性。
6.普适性
它不仅适用于两个物体所组成的系统,也适用于多个物体组成的系统;不仅适用于宏观物体组成的系统,也适用于微观粒子组成的系统。
临界与极值问题的解法:
在动量守恒定律的应用中,常常会遇到相互作用的两物体相距最近、避免相碰和物体开始反向运动等临界问题。分析临界问题的关键是寻找临界状态,临界状态的出现是有条件的,这种条件就是临界条件。临界条件往往表现为某个(或某些)物理量的特定取值。在与动量相关的临界问题中,临界条件常常表现为两物体的相对速度关系与相对位移关系,这些特定关系的判断是求解这类问题的关键。
“人船模型”的解题规律:
“人船模型”是动量守恒定律的拓展应用,它把速度和质量的关系推广到质量和位移的关系,这样给我们提供了一种解题思路和解决问题的方法。人船问题的适用条件是:两个物体组成的系统(当有多个物体组成系统时,可以先转化为两个物体组成的系统)动量守恒,系统的合动量为零。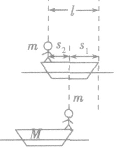
这种模型中涉及两种题型,一种题型是求解某物体在相互作用过程中通过的位移,此题型中需根据动量守恒、位移关系得到两个关系求解,如在图中,人从船头走到船尾时由动量守恒可得: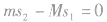
再由图中几何关系有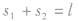
可得人船的位移分别为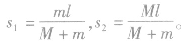
另一种题型是求某一时刻物体的速度,这种题型是先要由动量守恒求得两物体的一个速度关系,再由能量守恒得到两物体的另一个速度关系,从而求得物体的瞬时速度(或与瞬时速度相关的物理量)。
物质波:
| 经典粒子与经典波 | 经典粒子:任意时刻的确定的位置和速度以及时空中的确定的轨道,是经典物理学中粒子运动的基本特征 |
| 经典波:具有波长和频率,即在空间与时间上具有周期性 | |
| 物质波 | 德布罗意认为,任何一个运动着的物体,都有一种波与之相伴随,其波长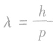 ,p是物体的动量,h是普朗克常量。人们把这种波称为物质波,也称为德布罗意波 ,p是物体的动量,h是普朗克常量。人们把这种波称为物质波,也称为德布罗意波 |
| 概率波 | 在现代物理中,微观粒子的运动不具有确定的位置和动量,没有轨迹的慨念。某时刻粒子在空间任一点都有可能出现,只是在不同位置出现的概率不同。粒子在空间出现的概率遵从波动规律,这种感觉波就成为概率波 |
| 不确定关系 | 利用数学方法对微观粒子的运动进行分析可以知道,如果以缸表示粒子位置的不确定量,以 △P表示粒子在x方向上的动量的不确定量,那么 式中h为普朗克常量 式中h为普朗克常量 |
| 备注 | (1)宏观物体观察不到其波动性的原因是其波长太短,波动性太弱 (2)物质波是概率波 (3)光波也是概率波 (4)对于光,先有波动理论(v和λ),其后在量子理论中引入了光子的能量E和动量p来补充它的粒子性。对于实物粒子,则先有粒子概念(E和p),再引用德布罗意波的概念来补充它的波动性 |
1、定义:原子核在其他粒子的轰击下产生新原子核的过程。所有核反应的反应前后都遵守:质量数守恒、电荷数守恒。
2、原子核的人工转变
①质子的发现:用α粒子轰击氮,
②电子的发现:用α粒子轰击铍,
与“在衰变中常伴有一种称为“中微子”的例子放出。中微子的性质十...”考查相似的试题有:
- 如图,质量为的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下...
- 如图,一质量为M的物块静止在光滑水平桌面的边缘,桌面离水平面的高度为h,一质量为m的子弹以水平速度v0射入物块后,以水平速...
- 如图所示,以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内,一滑板静止在光滑水平地面 上,左端紧靠B点,上表面所在...
- 质量为m=100kg的小船静止在水面上,水的阻力不计,船上左、右两端各站着质量分别为m甲=40kg,m乙=60kg的游泳者,当甲朝左...
- 在中子衍射技术中,常利用热中子研究晶体的结构,因为热中子的德布罗意波长与晶体中原子间距相近。已知中子质量m=1.67×10-27k...
- 不定项选择下列说法正确的是( )A.比结合能小的原子核结合成比结合能大的原子核时一定吸收核能B.一定强度的入射光照射某金...
- 如图所示为EAST部分装置的简化模型:垂直纸面的有环形边界的匀强磁场b区域,围着磁感应强度为零的圆形a区域,a区域内的离子向...
- 一个质子和一个中子聚变结合成一个氘核,同时辐射一个γ光子,已知质子、中子、氘核的质量分别为m1、m2、m3,普朗克常量为h,...
- 在人类认识原子与原子核结构的过程中,符合物理学史的是( )A.查德威克通过研究阴极射线发现了电子B.汤姆生首先提出了原子...
- 1919年,卢瑟福用α粒子轰击氮核发现质子.科学研究表明其核反应过程是:α粒子轰击静止的氮核后形成了不稳定的复核,复核发生...