本试题 “用动力臂是阻力臂3倍的杠杆,将重600N 的物体抬高40cm ,手向下压杠杆的力是250N ,手下降的高度是 cm ,人做的功是 J ,机械效率是 。” 主要考查您对功的计算
杠杆的机械效率
杠杆的平衡条件
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 功的计算
- 杠杆的机械效率
- 杠杆的平衡条件
功(W)等于力(F)跟物体在力的方向上通过的距离(s)的乘积。(功=力×距离),W=FS。
单位:
国际单位制中,力的单位是N,距离的单位是m,功的单位是N·m,它有一个专用名称叫做焦耳,简称焦,用符号J表示,1J=1N·m。
在利用该公式进行计算时的注意点:
(1)力与物体移动的距离在方向上必须一致;
(2)力与物体移动的距离必须对应于同一物体;
(3)力与物体移动的距离必须对应于同一段时间。
| 有用功 | W有用=Gh |
| 总功 | W总=Fs |
| 额外功 | W额外=W总-W有用 |
| 机械效率 | 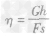 |
测量杠杆的机械效率:
【器材】
轻质杠杆(木质),重质杠杆(铁制),钩码,有支座的木板,弹簧秤,细线。
【操作】
(1)将轻质杠杆按如图装在画有等间距水平横线的木板上。在杠杆的A处悬挂几个钩码,把弹簧秤系在杠杆B处并竖直缓慢地向上拉杠杆。记下钩码重G1、钩码被提升的高度h1、弹簧秤的示数F1和弹簧秤移动的距离S1,比较G1h1和F1S1的大小,并根据η1=(G1h1)/(F1S1)算出此时杠杆的效率η1。
(2)减少悬在A处的钩码个数,重复上述实验,算出杠杆的效率η2。
比较η1和η2的大小,得η2<η1,表明同一杠杆在不同情况下,效率可能不同。
(3)用重质杠杆代替轻质杠杆重复(1),算出杠杆的效率η3。比较η1和η3的大小,得η1>η3,可知不同杠杆在相同工作情况下,效率也可能不同。
简单分析η1、η2、η3大小不同的原因。
杠杆的平衡条件:
动力×动力臂=阻力×阻力臂。
即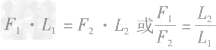
在杠杆平衡时,动力臂是阻力臂的几倍,动力就是阻力的几分之几。
利用杠杆平衡条件来分析和计算有关问题,一般遵循以下步骤:
(1)确定杠杆支点的位置。
(2)分清杠杆受到的动力和阻力,明确其大小和方向,并尽可能地作出力的示意图。
(3)确定每个力的力臂。
(4)根据杠杆平衡条件列出关系式并分析求解。
例:如图所示,AOB为一机械设备的简化示意图,我们可以把它看成杠杆(自重不计),已知AO= 2OB。固定D点,使OB处于水平位置,此时B端挂一重为40N的物体,要使杠杆不发生转动,至少需在A端施加F=____N的力,在图上画出此时力F的方向。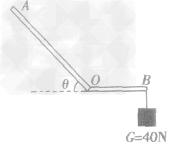
解析:要想得到施加在A点的最小力,就要找到最大力臂,由图可知,最大力臂应是OA,故过A点作们的垂线,方向斜向下即为最小力。据杠杆平衡条件得:F·OA=G·OB,代入数值为F×2OB=40N×OB,解方程得F=20N。
答案:20 力F的方向如图
实验法探究杠杆平衡条件:
实验前要调节杠杆的平衡螺母使其在水平位置上平衡,目的是使杠杆的重心落在支点上,从而消除杠杆的重力对平衡的影响。当杠杆水平平衡时,O点距悬挂钩码处的距离便是力臂,而且可用杠杆上的“格数”代替力臂大小。
例:我们都做过“探究杠杆平衡条件”的实验。
(1)实验没有挂钩码时,若杠杆左端下倾,则应将右端的平衡螺母向____(选填“左”或“右”)调节,使杠杆在水平位置平衡。实验前使杠杆水平平衡的目的是____.
(2)实验中,用图所示的方式悬挂钩码,杠杆也能水平平衡(杠杆上每格等距),但老师却提醒大家不要采用这种方式。这主要是因为该种方式( )
A.一个人无法独立操作
B.需要使用太多的钩码
C.力臂与杠杆不重合
D.力和力臂数目过多
(3)图中,不改变支点O右侧所挂的两个钩码及其位置,保持左侧第____格的钩码不动,将左侧另外两个钩码改挂到它的下方,杠杆仍可以水平平衡。 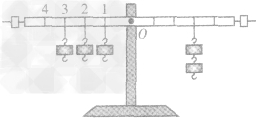
解析:(1)实验前要调节杠杆的平衡螺母使其在水平位置平衡,目的是方便地测量力臂。调节方法是将平衡螺母向杠杆偏高的一端调,即哪端轻向哪端调。
(2)探究杠杆平衡条件时,用的力和力臂数目过多,每个力都会给杠杆转动带来影响,给探究过程带来麻烦。
(3)根据杠杆平衡条件 ,即
,即
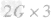 ,所以l1=2(格)。
,所以l1=2(格)。
答案:(1)右方便地测量力臂(2)D(3)2
利用杠杆平衡条件求最小力的方法:
由公式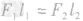 可知,当阻力、阻力臂一定时,动力臂越长,动力越小。当动力臂最长时,动力最小。要求最小动力,必须先画出最大动力臂。
可知,当阻力、阻力臂一定时,动力臂越长,动力越小。当动力臂最长时,动力最小。要求最小动力,必须先画出最大动力臂。
1.寻找最大动力臂的方法
(1)当动力作用点确定后,支点到动力作用点的线段即为最大动力臂;
(2)动力作用点没有规定时,应看杠杆上哪一点离支点最远,则这一点到支点的距离即为最大动力臂。
2.作最小动力的方法
(1)找到最大动力臂后,过作用点作动力臂的垂线;
(2)根据实际,动力能使杠杆沿阻力作用的反方向转动,从而确定动力的方向。
与“用动力臂是阻力臂3倍的杠杆,将重600N 的物体抬高40cm ,手向...”考查相似的试题有:
- 老人和小孩一同爬楼,小孩比老人先到楼顶,则小孩一定比老人( )A.做功少B.做功多C.做功块D.做功慢
- 下列数据中,最符合实际情况的是( ) A.一枚鸡蛋的质量50g B.将一瓶矿泉水从地面拿到桌面需做功50J C.洗澡时的水温70℃ D...
- 2007年4月18日,新型高速列车“和谐”号动车组开始驰骋在主要铁路线上,从而拉开了全国铁路第六次大提速的大幕.如图所示的CRH2...
- 如图中小朋友用力推车,虽然累得满头大汗,可是车却一动不动,小孩有无做功?_____________________________________________...
- 如图所示,用一动滑轮将重为1200N的物体A沿水平方向匀速移动,物体A与水平的摩擦力为300N,此时动滑轮的机械效率为80%.求:...
- 在“研究杠杆平衡条件”的实验中(1) 实验前,发现杠杆处于如图所示位置,为了使杠杆在水平位置平衡,应将杠杆右端的平衡螺母...
- 如图所示,物体的物重是G,在下列三种情况下,杠杆处于平衡状态,当杠杆、滑轮的物重及摩擦不计时,拉力F1=____;F2=____;F3...
- 弹簧测力计量程为5N。给你一支铅笔,铁丝和铁钉(如图所示),请你将它的量程改为15 N。请画图(将装置图画在方框内)说明做法...
- 小森在“探究杠杆平衡条件”的实验中:(1)把杠杆挂在支架上,观察到杠杆左端下沉,当他去调节螺母时,发现两侧螺母已丢失,聪明...
- 小阳同学用一个左右各为12格的杠杆,如图所示,一个量程为5N,分度值为0.2 N的弹簧测力计做动力,一个重为6N的重物做阻力,两...