本试题 “如图所示,质量分别为m1、m2的两个小球A、B,带有等量异种电荷,通过绝缘轻质弹簧相连接,置于绝缘光滑的水平面上,突然加一水平向右的匀强电场后,两球A、B...” 主要考查您对弹力的大小、胡克定律
动量守恒定律
电场强度的定义式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 弹力的大小、胡克定律
- 动量守恒定律
- 电场强度的定义式
弹力的大小:
弹力的大小与物体的形变程度有关,形变量越大,产生的弹力越大;形变量越小,产生的弹力越小。
(1)一般情况下,弹力的大小可以利用平衡条件或牛顿运动定律计算出来;对于弹簧的弹力,在弹性限度内遵循胡克定律:
(2)胡克定律在弹性限度内,弹簧的弹力和其形变量(伸长或缩短的长度)成正比,即F=kx,式中k为劲度系数,x为弹簧的形变量,F为弹力。
胡克定律的图像如图所示。 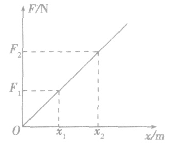
①式中形变量是指在弹性限度内发生的。形变量x是弹簧在原长基础上的改变量,即弹簧伸缩后的长度L与原长L0的差:x=|L—L0|,不能将x当做弹簧的长度。
②胡克定律中劲度系数k的单位是N/m,由弹簧自身的条件(材料、长度、横截面积)决定,弹簧做好后,劲度系数是确定的。不同弹簧的劲度系数一般不同。
③劲度系数k的两种求法
a.由胡克定律F=kx知:k=F/x
b.由F一x图像知: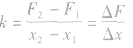
判定弹力的有无及其方向的方法:
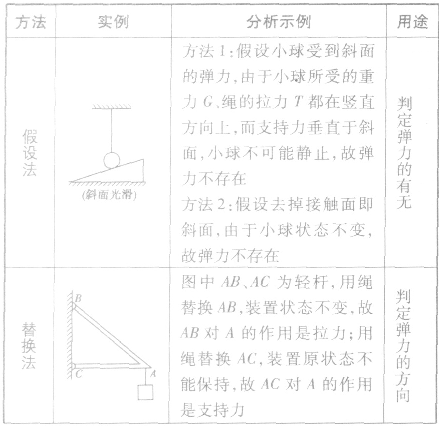
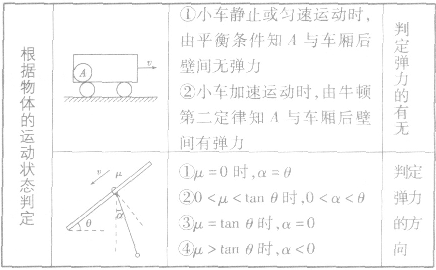
1、内容:一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变。
2、表达式:m1v1+m2v2=m1v1'+m2v2'。
3、动量守恒定律成立的条件:
①系统不受外力或系统所受外力的合力为零;
②系统所受的外力的合力虽不为零,但系统外力比内力小得多,如碰撞问题中的摩擦力,爆炸过程中的重力等外力比起相互作用的内力来小得多,可以忽略不计;
③系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变。
4、动量守恒的速度具有“四性”:
①矢量性;②瞬时性;③相对性;④普适性。
动量守恒定律与机械能守恒定律的比较:



系统动量守恒的判断方法:
方法一:南动量守恒的条件判断动量守恒的步骤如下:
(1)明确系统由哪几部分组成。
(2)对系统中各物体进行受力分析,分清哪些是内力,哪些是外力。
(3)看所有外力的合力是否为零,或内力是否远大于外力,从而判断系统的动量是否守恒。
方法二:南系统动量变化情况判断动量守恒方法如下:
(1)明确初始状态系统的总动量是多少。
(2)对系统内的物体进行受力分析、运动分析,确定每一个物体的动量变化情况。
(3)确定系统动量变化情况,进而判定系统的动量是否守恒。
电场强度:


计算场强的四种方法:
1.计算电场强度的常用方法——公式法
(1)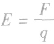 是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
(2)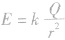 要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
(3)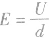 是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
2.计算多个电荷形成的电场强度的方法——叠加法
当空间的电场由几个点电荷共同激发的时候,空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和,其合成遵循矢量合成的平行四边形定则。
3.计算特殊带电体产生的电场强度的方法
(1)补偿法对于某些物理问题,当直接去解待求的A很困难或没有条件求解时,可设法补上一个B,补偿的原则是使A+B成为一个完整的模型,从而使A+B变得易于求解,而且,补上去的B也必须容易求解。这样,待求的A便可从两者的差值中获得,问题就迎刃而解了,这就是解物理题时常用的补偿法。用这个方法可算出一些特殊的带电体所产生的电场强度。
(2)微元法在某些问题中,场源带电体的形状特殊,不能直接求解场源带电体在空间某点所产生的总电场,此时可将场源带电体分割,在高中阶段,这类问题中分割后的微元常有部分微元关于待求点对称,这就可以利用场的叠加及对称性来解题。
4.计算感应电荷产生的电场强度的常用方法—— 静电平衡法根据静电平衡时导体内部场强处处为零的特点,外部场强与感应电荷产生的场强(附加电场)的合场强为零,可知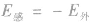 ,这样就可以把复杂问题变简单了。
,这样就可以把复杂问题变简单了。
与“如图所示,质量分别为m1、m2的两个小球A、B,带有等量异种电...”考查相似的试题有:
- A、B两球质量分别为m1与m2,用一劲度系数为k的弹簧相连,一长为L1的细线与m1相连,置于水平光滑桌面上,细线 的另一端拴在竖...
- 如图所示,m与M、M与地面之间均光滑,当m沿斜面下滑时,对m和M组成的系统有( )A.机械能守恒B.动量守恒C.m的重力势能的减...
- 如图所示,水平地面上放着一个内表面光滑的凹槽,槽两端固定有两轻质弹簧,一弹性小球在两弹簧间往复运动,把槽、小球和弹簧...
- 在水平桌面上沿一条直线放两个完全相同的小物块A和B(可看作质点)质量均为m,它们相距s.B到桌边的距离是2s.对A施以瞬间水...
- 关于电场强度,正确的是( )A.电场强度的大小与检验电荷的电量成反比B.电场强度的方向与检验电荷的正负有关C.电场强度大...
- 在静电场中A.电场强度处处为零的区域内,电势也一定处处为零B.电场强度处处相等的区域内,电势也一定处处相等C.电场强度的...
- 对于电场中的某一点,下列各量中,与检验电荷无关的物理量是A.电场力FB.电场强度EC.电势能EpD.电场力做的功W
- A点的电场强度E=2.0×104N/C,将电荷量Q=+2.O×10-8C的点电荷放在A点。求该点电荷在A点所受静电力F的大小。
- 空间存在电场,在x轴上A点处,放一个电荷量大小为2.0×10-6C的负点电荷q1,q1受到的电场力F1=1.4×10-2N,沿+x方向.(1)求A点...
- 判断下列说法正确的是[ ]A.电荷在电场中某点受到的电场力大,该点的电场强度就大B.电场强度的方向总跟电场力的方向一致C....