本试题 “如图所示,由导体棒ab和矩形线框cdef组成的“10”图案在匀强磁场中一起向右匀速平动,匀强磁场的方向垂直线框平面向里,磁感应强度B随时间均匀增大,则下列说法...” 主要考查您对右手定则
法拉第电磁感应定律
导体切割磁感线时的感应电动势
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 右手定则
- 法拉第电磁感应定律
- 导体切割磁感线时的感应电动势
| 内容 | 伸开右手,大拇指跟其余四指垂直,并且都跟手掌在同一平面内,让磁感线垂直穿入掌心,大拇指指向导体运动的方向,其余四指所指的方向,就是感应电流的方向 |
| 适用范围 | 导体切割磁感线 |
| 相对性 | 在右手定则中,导体运动的方向是指导体切割磁感线的方向,即导体相对磁场的运动方向,如图中,磁场以速度v1向右运动,导体棒以速度v2也向右运动,若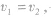 导体棒相对磁场静止,不切割磁感线,若 导体棒相对磁场静止,不切割磁感线,若 导体棒向右切割磁感线,大拇指需指向右方,但若 导体棒向右切割磁感线,大拇指需指向右方,但若 ,导体棒向左切割磁感线,大拇指需指向左方 ,导体棒向左切割磁感线,大拇指需指向左方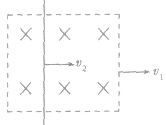 |
| 备注 | 当导体切割磁感线但回路中磁通量不变时,回路中没有电流,但切割磁感线的那部分导体仍是要产生电动势的,右手定则所判定的方向就是所产生的电动势的方向(在电源内部由负极指向正极的方向,也是该电源使电流流动的方向) |
右手定则与左手定则的区别:
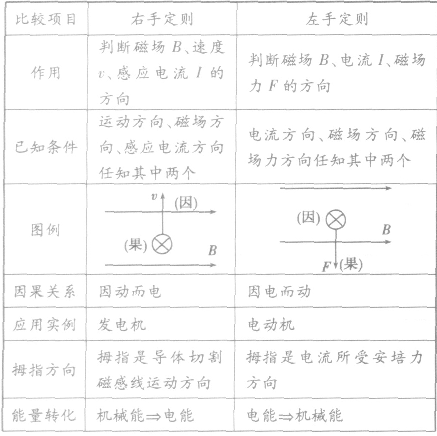

法拉第电磁感应定律:
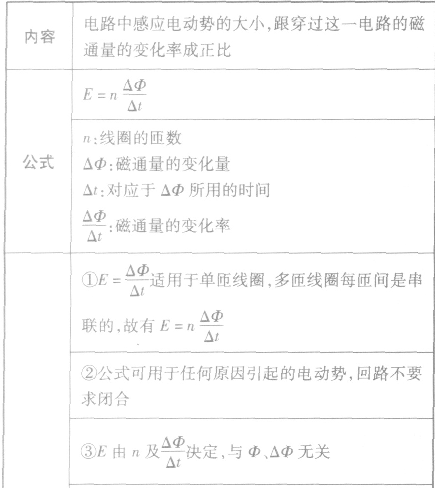

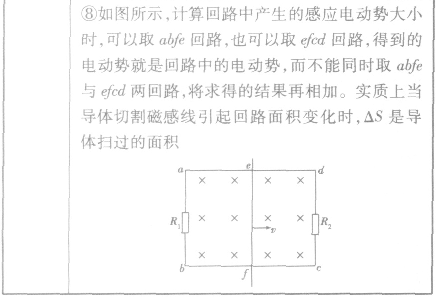
导体切割磁感线的两个特例:

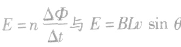 的区别与联系及选用原则:
的区别与联系及选用原则: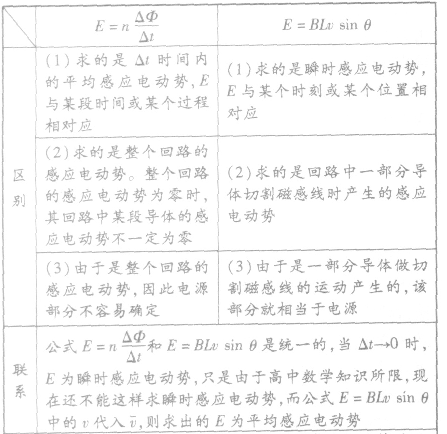

电磁感应中动力学问题的解法:
电磁感应和力学问题的综合,其联系的桥梁是磁场对感应电流的安培力,因为感应电流与导体运动的加速度有相互制约的关系。
1.分析思路
(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向。
(2)求回路中的电流。
(3)分析研究导体受力情况(包含安培力,用左手定则确定其方向)。
(4)列动力学方程或平衡方程求解。
2.常见的动态分析这类问题中的导体一般不是做匀变速运动,而是经历一个动态变化过程再趋于一个稳定状态,故解这类问题时正确进行动态分析确定最终状态是解题的关键。同时也要抓好受力情况和运动情况的动态分析,研究顺序为:导体受力运动产生感应电动势一感应电流一通电导体受安培力一合外力变化一加速度变化一速度变化一周而复始地循环,循环结束时,加速度等于零.导体达到稳定运动状态。
电磁感应中的动力学临界问题:
(1)解决这类问题的关键是通过运动状态的分析,寻找过程中的临界状态,如速度、加速度求最大值或最小值的条件。
(2)基本思路: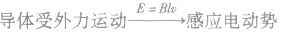
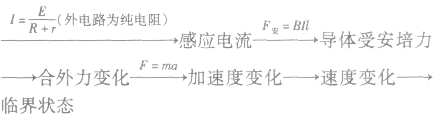
导体切割磁感线产生的电动势:
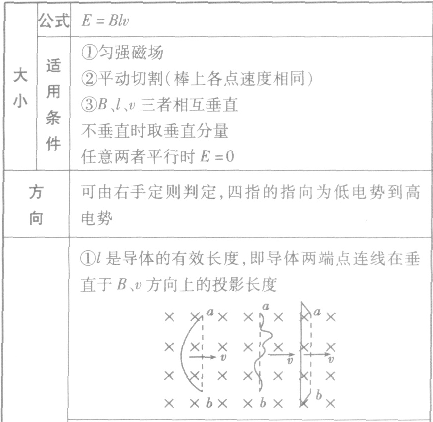
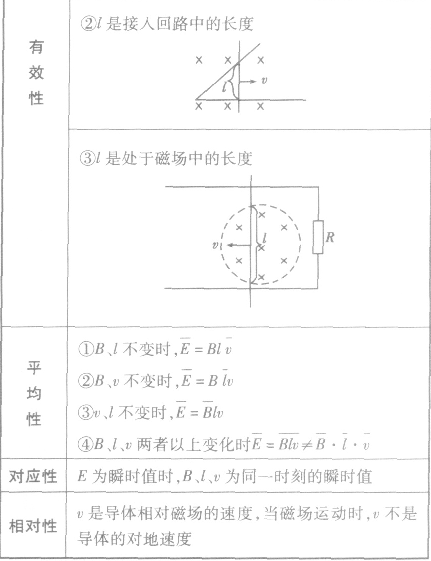
电磁感应中电路问题的解法:
电磁感应规律与闭合电路欧姆定律相结合的问题,主要涉及电路的分析与计算。解此类问题的基本思路是:
(1)找电源:哪部分电路产生了电磁感应现象,则这部分电路就是电源。
(2)由法拉第电磁感应定律求出感应电动势的大小,根据楞次定律或右手定则确定出电源的正负极。
①在外电路,电流从正极流向负极;在内电路,电流从负极流向正极。
②存在双感应电动势的问题中,要求出总的电动势。
(3)正确分析电路的结构,画出等效电路图。
①内电路:“切割”磁感线的导体和磁通量发生变化的线圈都相当于“电源”,该部分导体的电阻相当于内电阻。
②外电路:除“电源”以外的电路即外电路。
(4)运用闭合电路欧姆定律、串并联电路特点、电功率等列方程求解。
与“如图所示,由导体棒ab和矩形线框cdef组成的“10”图案在匀强磁...”考查相似的试题有:
- 如图所示,光滑平行金属导轨PP'和OO',都处于同一水平面内,P和Q之间连接一电阻R。整个装置处于竖直向下的匀强磁场中。现垂直...
- 如图所示,N、S两极间有闭合电路的一部分导体在做切割磁感线运动,其中(C)导体垂直纸面向里运动,(D)导体垂直纸面向外运...
- 如图所示,面积为S的矩形线圈共N匝,线圈总电阻为R,在磁感应强度为B、方向垂直纸面向里的匀强磁场中以竖直线OO′为轴,以角速...
- 如图所示,交流发电机转子有n匝线圈,每匝线圈所围面积为S,匀强磁场的磁感应强度为B,匀速转动的角速度为ω,线圈总电阻为r,...
- 一闭合线圈有50匝,总电阻R=20Ω,穿过它的磁通量在0.1s内由8×10-3Wb增加到,则线圈中的感应电动势E= ,线圈中的平均电流强...
- 如图所示,一对平行放置的金属板M、N的中心各有一小孔P、Q,PQ连线垂直金属板;N板右侧的圆形区域A内分布有方向垂直于纸面向...
- 如图(a)为某实验小组利用微电流传感器在做验证楞次定律DIS实验时在计算机屏幕上得到的波形图,某横坐标为时间t,纵坐标为电...
- 如图所示,宽为L=0.5m、足够长的平行金属导轨MN和M’N’固定在倾角为θ=37°的斜面上,在N和N’之间连有一个0.8Ω的电阻R.在导轨上...
- 一个边长为L的正方形导线框在倾角为θ的光滑固定斜面上由静止开始沿斜面下滑,随后进入虚线下方方向垂直于斜面的匀强磁场中....
- 如图所示,AB、CD是两根足够长的光滑固定平行金属导轨,两导轨间的距离为L,导轨平面与水平面的夹角为θ,在整个导轨平面内都...