本试题 “在数列{an}和{bn}中,a1=1,b1=2,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列(n∈N*),(1)求a2,a3,a4和b2,b3,b4;(2)猜想{an},{bn}的通...” 主要考查您对等差中项
等比中项
数学归纳法证明不等式
数学归纳法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差中项
- 等比中项
- 数学归纳法证明不等式
- 数学归纳法
等差中项:
若a,A,b成等差数列,那么A叫做a与b的等差中项,且2A=a+b,即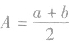 ,反之,若
,反之,若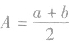 ,则a,A,b成等差数列。
,则a,A,b成等差数列。
等差数列中相邻三项之间存在如下关系:
(1)
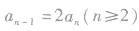 反之,若数列中相邻三项之间存在如下关系:
反之,若数列中相邻三项之间存在如下关系: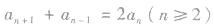 则该数列是等差数列,
则该数列是等差数列,
(2) 若a,A,b成等差数列,那么 2A=a+b,A-a =b -A,a-A =A -b都是等价的.
2A=a+b,A-a =b -A,a-A =A -b都是等价的.
等比中项:
若数a,G,b成等比数列,那么就称G为a与b的等比中项,从而有G2=ab或G=±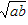 。
。
等比中项的理解:
如果a,G,b三个数成等比数列,则有G2=ab.反之不一定成立.由等比中项定义可知: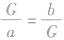 ,
, 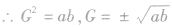 ,
,
这表明,只有同号的两项才有等比中项,并且这两项有2个互为相反数的等比中项,当a>0,b>0时,G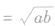 又叫做a,b的几何平均数。
又叫做a,b的几何平均数。
归纳法的定义:
由有限多个个别的特殊事例得出一般结论的推理方法,称为归纳法。
数学归纳法证明不等式的步骤:
(1)证明当n取初始值n0(例如n0=0,n0=1等)时不等式成立;
(2)假设当n=k(k为自然数,k≥n0)时不等式成立,证明当n=k+1时不等式也成立。
对数学归纳法的理解:
(1)数学归纳法是一种用于证明与自然数n有关的命题的正确性的证明方法.它的操作步骤简单、明确。
(2)运用数学归纳法证明与正整数有关的数学命题,两个步骤缺一不可.理解数学归纳法中的递推思想,尤其要注意其中第二步,证明n=k+1命题成立时必须要用到n=k时命题成立这个条件.这种理解不仅使我们能够正确认识数学归纳法的原理与本质,也为证明过程中第二步的设计指明了思维方向.
归纳法:
对于某类事物,由它的一些特殊事例或其全部可能情况,归纳出一般结论的推理方法叫做归纳法。归纳法包括完全归纳法和不完全归纳法。
数学归纳法:
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
(1)证明当n取第一个值n0(n0∈N*)时命题成立;
(2)假设当n=k(k∈N*,k≥n0)时命题成立,证明当n=k+1时命题也成立;
完成这两步,就可以断定这个命题对从n0开始的所有正整数n都成立,这种证明方法叫做数学归纳法。
数学归纳法的特点:
①用数学归纳法进行证明时,要分两个步骤,两步同样重要,两步骤缺一不可;
②第二步证明,由假设n=k时命题成立,到n=k+1时.必须用假设条件,否则不是数学归纳法;
③最后一定要写“由(1)(2)……”。
数学归纳法的应用:
(1)证明恒等式;
(2)证明不等式;
(3)三角函数;
(4)计算、猜想、证明。
与“在数列{an}和{bn}中,a1=1,b1=2,且an,bn,an+1成等差数列...”考查相似的试题有:
- △ABC中,角A,B,C所对的边分别为a,b,c,若a,b,c成等差数列,∠B=30°,,那么b=( )。
- 如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+...+a7=A.28B.21C.14D.35
- 在等差数列{an}中,若a1+a5+a9=,则sin(a4+a6)= [ ]A、B、C、0D、
- 已知α1,α2,…αn∈(0,π),n是大于1的正整数,求证:|sin(α1+α2+…+αn)|<sinα1+sinα2+…+sinαn。
- 用数学归纳法证明:()的过程中,从“到”左端需增加的代数式为 ( )
- 从中得出的一般性结论是________
- 已知f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:f(a·b)=af(b)+bf(a), (Ⅰ)求f(0),f(1)的值...
- 有一个奇数列1,3,5,7,9,┅,现在进行如下分组:第一组含一个数{1},第二组含两个数{3,5},第三组含三个数{7,9,11},第...
- 已知数列{an}的通项公式为an=n+12,n=2k-1(k∈N*)2n2,n=2k(k∈N*),设bn=a2n-1a2n,Sn=b1+b2+…+bn.(1)求Sn;(2)证明:当n...
- 已知△ABC的三边长为有理数。(1)求证:cosA是有理数;(2)求证:对任意正整数n,cosnA是有理数。