本试题 “在军事演习中,某空降兵从飞机上跳下,先做自由落体运动,t1时刻,速度达最大值v1时打开降落伞,做减速运动,在t2时刻以较小速度v2着地.他的速度图象如图所...” 主要考查您对平均速度和瞬时速度的区别
功
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 平均速度和瞬时速度的区别
- 功
平均速度:
质点在某段时间内的位移与发生这段位移所用时间的比值叫做这段时间(或位移)的平均速度v,即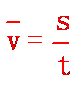 ,平均速度是矢量,其方向跟位移方向相同.平均速度是对变速运动的粗略描述。
,平均速度是矢量,其方向跟位移方向相同.平均速度是对变速运动的粗略描述。
瞬时速度:
运动物体在某一时刻(或经过某一位置)的速度,方向沿轨迹上质点所在点的切线方向指向前进的一侧,瞬时速度是对变速运动的精确描述,其大小叫速率。
平均速率:
物体在某段时间内通过的路程l跟通过这段路程所用的时间t的比值,叫做这段路程(或这段时间)的平均速率,即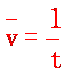 ,它是标量,值得注意的是:它并不是平均速度的大小.
,它是标量,值得注意的是:它并不是平均速度的大小.
平均速度和瞬时速度对比:
(1)区别:平均速度反映的是物体在整个运动过程中的整体运动情况,而瞬时速度反映的是物体在运动过程的某一时刻或某一位置的运动情况;
(2)联系:在匀速直线运动中,任何时刻的瞬时速度和整个运动过程中的平均速度相同。
方法与知识感悟:
平均速度是反映的某一段运动过程中的平均运动快慢,是这一过程中的位移与时间的比值( 是平均速度的定义式),适用于所有的运动;而
是平均速度的定义式),适用于所有的运动;而 适用于匀变速直线运动,但若
适用于匀变速直线运动,但若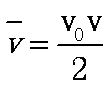 ,却不能判定该物体做匀变速直线运动.
,却不能判定该物体做匀变速直线运动.
平均速度的计算:
一辆汽车沿平直公路行驶,先以速度v1通过前的位移,再以速度v2=50km/h通过其余的位移.若整个位移中的平均速度=37.5km/h,则第一段位移内的平均速度是多少?
解:设整段位移为x,通过前位移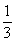 和后位移
和后位移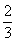 的时间分别为t和t
的时间分别为t和t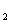 ,根据
,根据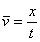 得
得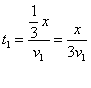 ,
,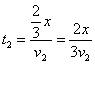 ,可得
,可得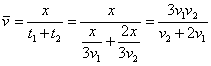 。解得第一段时间位移内的速度
。解得第一段时间位移内的速度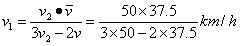 =25km/h。
=25km/h。
功:
1、功的定义:力和作用在力的方向上通过的位移的乘积。是描述力对空间积累效应的物理量,是过程量。
2、功的两个必要因素:作用在物体上的力;物体在力的方向上发生的位移。
3、功的定义式:W=Fscosα,其中F是恒力,s是作用点的位移,α是力与位移间的夹角(功的单位焦耳,简称焦,符号J)。
4、功的计算
①恒力的功可根据W=FScosα进行计算,本公式只适用于恒力做功;
②根据W=P·t,计算一段时间内平均做功;
③利用动能定理计算力的功,特别是变力所做的功;
④根据功是能量转化的量度反过来可求功。
力做功情况的判定方法:
一个力对物体做不做功,是做正功还是做负功,判断的方法是:
(1)看力与位移之间的夹角,或者看力与速度之间的夹角:为锐角时,力对物体做正功;为钝角时,力对物体做负功;为直角时,力对物体不做功。
(2)看物体间是否有能量转化:若有能量转化,则必定有力做功。此方法常用于相连的物体做曲线运动的情况。
变力做功的求法:
公式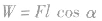 只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
1.用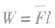 求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用
求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用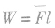 求变力F所做的功。其平均值大小 为
求变力F所做的功。其平均值大小 为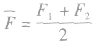 ,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
2.用微元法(或分段法)求变力做功变力做功时,可将整个过程分为几个微小的阶段,使力在每个阶段内不变,求出每个阶段内外力所做的功,然后再求和。当力的大小不变而方向始终与运动方向间的夹角恒定时,变力所做的功形: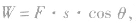 其中s是路程。
其中s是路程。
3.用等效法求变力做功若某一变力做的功等效于某一恒力做的功,则可以应用公式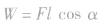 来求。这样,变力做功问题就转化为了恒力做功问题。
来求。这样,变力做功问题就转化为了恒力做功问题。
4.用图像法求变力做功存F—l图像中,图线与两坐标轴所围“面积”的代数和表示F做的功,“面积”有正负,在l轴上方的“面积”为正,在l轴下方的“面积”为负。
5.应用动能定理求变力做功
如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能变化量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
6.利用功能关系求变力做功
在变力做功的过程中,当有重力势能、弹性势能以及其他形式的能量参与转化时,可以考虑用功能关系求解。因为做功的过程就是能量转化的过程,并且转化过程中能量守恒。
7.利用W=Pt求变力做功
这是一种等效代换的观点,用W=Pt计算功时,必须满足变力的功率是恒定的。若功率P是变化的,则需用 计算,其中当P随时间均匀变化时,
计算,其中当P随时间均匀变化时, 。
。
与“在军事演习中,某空降兵从飞机上跳下,先做自由落体运动,t1...”考查相似的试题有:
- 一辆汽车以速度v行驶了全程的一半,然后匀减速行驶了后一半,恰好停止,全程的平均速度为( )A.v2B.2v3C.v2D.v3
- 试判断下列几个速度中哪个是平均速度( )A.子弹出枪口的速度800m/sB.小球第3s末的速度6m/sC.汽车从甲站行驶到乙站的速度4...
- 某中学正在举行班级对抗赛,张明明同学是短跑运动员,在百米竞赛中,测得他在5 s末的速度为10.4m/s,10 s末到达终点的速度为1...
- 不定项选择下列关于速度的叙述中,属于瞬时速度的是( )A.火车以76km/h的速度通过南京长江大桥B.子弹以600m/s的速度从枪口...
- 在平直公路上行驶的汽车中,某人从车窗相对于车静止释放一个小球,不计空气阻力,用固定在路边的照相机对小球进行闪光照相....
- 如图所示,质量为M的物体放在光滑水平地面上,受与水平方向成α角的恒定拉力F作用,从静止开始沿水平地面运动,在时间t内,拉...
- 用起重机把重量为2.0×104N的物体以2m/s的速度匀速地提高了5m,则A.钢绳的拉力做正功为1.0×105JB.重力对物体做正功为1.0×...
- 如图所示,竖直平面内放一直角杆,杆的水平部分粗糙,竖直部分光滑,两部分各套有质量分别为mA=2.0kg和mB=1.0kg的小球A和B,A...
- 在距地面10 m高处,一人以50 m/s的速度水平抛出一个质量为4 kg的物体,物体落地时速度大小仍然是50 m/s,则人抛出物体的过程...
- 某健身游戏过程可简化为如图所示物理模型.在平静的水面上,有一长L=12m的木船,木船右端固定一直立桅杆,木船和桅杆的总质量...