本试题 “如图所示,质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.2,现用F=25N与水平方向成θ=37°的力拉物体,使物体由静止开始做匀加速运动:(1)物体所受支持力为...” 主要考查您对力的分解
从受力确定运动情况
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 力的分解
- 从受力确定运动情况
力的合成与分解:
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
分解方法:
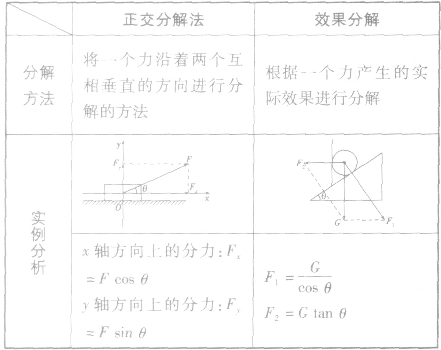
几种按效果分解的实例:


由力的三角形定则求力的最小值:
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值 。
。
(2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值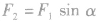 。
。
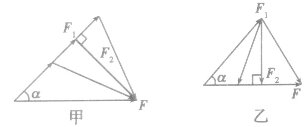
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值 。
。
由圆的切线求力方向的极值:
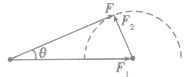
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足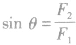 。
。 
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足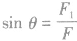 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足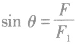 。
。
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
力的分解的几种情况:
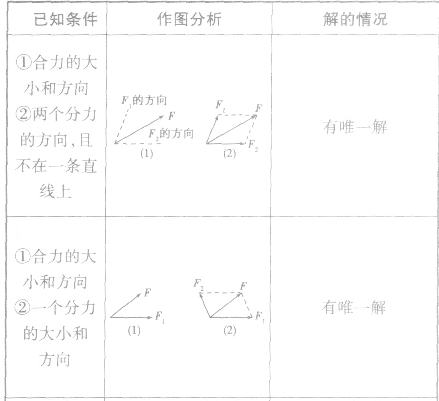
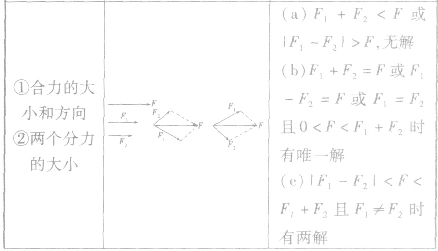
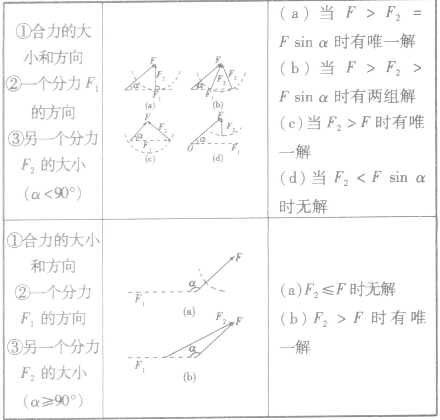
分解方法:

几种按效果分解的实例:


由力的三角形定则求力的最小值:
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值
 。
。 (2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值
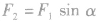 。
。
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值
 。
。由圆的切线求力方向的极值:
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足
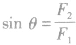 。
。 
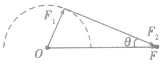
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足
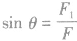 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足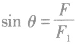 。
。
从受力确定运动情况:
1、知道物体受到的全部作用力,应用牛顿第二定律求加速度,再应用运动学公式求出物体的运动情况。
2、分析这两点问题的关键是抓住受力情况和运动情况的桥梁——加速度。
3、由物体的受力情况求解物体的运动情况的一般方法和步骤:
①确定研究对象,对研究对象进行受力分析,并画出物体的受力图;
②根据力的合成与分解的方法,求出物体所受的合外力(包括大小和方向);
③根据牛顿第二定律列方程,求出物体的加速度;
④结合给定的物体运动的初始条件,选择运动学公式,求出所需的运动参量,并分析讨论结果是否正确合理。
动力学中临界、极值问题的解决方法:
(1)在运用牛顿运动定律解决动力学有关问题时,常常会讨论相互作用的物体是否会发生相对滑动,相互接触的物体是否会发生分离等,这类问题就是临界问题。临界问题是指物体的运动性质发生突变,要发生而尚未发生改变时的状态。此时运动物体的特殊条件往往是解题的突破口。本部分中常出现的临界条件为:
①绳子或杆的弹力为零;
②相对静止的物体间静摩擦力达到最大,通常在计算中取最大静摩擦力等于滑动摩擦力;
③接触面间弹力为零,但接触物体的速度、加速度仍相等。临界状态往往是极值出现的时刻,题目中常出现隐含临界状态的词语,如“最大”“最小”“最短”“恰好”等.
(2)解决临界问题的关键是要分析出临界状态,例如两物体刚好要发生相对滑动时,接触面上必出现最大静摩擦力,两个物体要发生分离时,相互之间的作用力——弹力必定为零。
(3)解决临界问题的一般方法
①极限法:题设中若出现“最大”“最小…‘刚好”等这类词语时,一般就隐含着临界问题,解决这类问题时,常常是把物理问题(或物理过程)引向极端,进而使临界条件或临界点暴露出来,达到快速解决有关问题的目的。
②假设法:有些物理问题在变化过程中可能会出现临界问题,也可能不出现临界问题,解答这类问题,一般要用假设法。
③数学推理法:根据分析的物理过程列出相应的数学表达式,然后由数学表达式讨论出临界条件。
变加速运动过程的分析方法:
力可以改变速度的大小,也可以改变速度的方向。在牛顿运动定律的应用中,常常会出现物体在变力作用下,对物体的运动情况作出定性判断。处理此类问题的关键是抓住力或加速度与速度之间的方向关系,即同向加速,反向减速,而至于加速度变大或变小,只是影响速度改变的快慢,如在分析自由下落的小球,下落一段时间与弹簧接触后的运动情况时,从它开始接触弹簧到弹簧被压缩到最短的过程中,加速度和速度的变化情况讨论如下(过程图示如图).
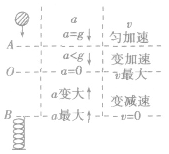
①小球接触弹簧上端后受两个力作用:向下的重力和向上的弹力,在接触后的前一阶段,重力大于弹力,合力向下,因为弹力F=kx不断增大,所以合力不断变小,故加速度也不断减小,由于加速度与速度同向,因此速度不断变大。
②当弹力逐渐增大到与重力大小相等时,合外力为零,加速度为零,速度达到最大。(注意:此位置是两个阶段的转折点)
③后一阶段,即小球到达上述平衡位置之后,由于惯性仍继续向下运动,但弹力大于重力,合力向上,且逐渐变大,因而加速度逐渐变大,方向向上,小球做减速运动,因此速度逐渐减小到零,到达最低点时,弹簧的压缩量最大。
发现相似题
与“如图所示,质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.2...”考查相似的试题有:
- 如下图所示,在水平粗糙横杆上,有一质量为m的小圆环A,用一细线悬吊一个质量为m的球B。现用一水平拉力缓慢地拉起球B,使细线...
- 在匀变速直线运动中,下列说法中正确的是( )A.匀变速直线运动的位移随时间均匀变化B.匀变速直线运动的速度随时间均匀变化C...
- 如图所示,质量为M的半球形容器静止在水平桌面上,质量为m的木块静止在容器内P点,O点为容器的球心,已知OP与水平方向的夹角...
- 两根长度相等的轻绳,下端悬挂一质量为m的物体,绳的上端分别固定在水平天花板上的M、N两点.M、N两点之间的距离为x,如图所示...
- 如图所示,横截面为直角三角形的斜劈A,放在粗糙的水平地面上,在劈与竖直墙壁之间放置一光滑球B,系统处于静止状态.若在球B...
- 一轮船以一定的速度垂直河岸向对岸开行,当河水流速均匀时,轮船所通过的路程、过河所用的时间与水流速度的正确关系是( )A...
- 如图所示,两个质量分别为m1=1kg、m2=4kg的物体置于光滑的水平面上,中间用轻质弹簧秤连接,两个大小分别为F1=30N、F2=20N的...
- 如图所示,从某一高处自由下落的小球,落至弹簧上端并将弹簧压缩到最短。问小球被弹簧弹起直至离开弹簧的过程中,小球的速度...
- 将一个质量为1kg的物块置于倾角为37°的固定斜面上,物块在与斜面夹角为30°的拉力F作用下加速上升,已知物块与斜面间的动摩擦...
- 如图所示为某小球所受的合力与时间的关系图象,各段的合力大小相同,作用时间相同,设小球从静止开始运动。由此可判定[ ]A....