本试题 “夏天暴雨前,往往会电闪雷鸣.其中雷声是由于云团之间放电引起空气的剧烈 ______产生的,如果在看到闪电后3s才听到雷声,已知当时气温为25℃.声音在空气中的...” 主要考查您对声音的产生
声速
密度公式的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 声音的产生
- 声速
- 密度公式的应用
声源:
正在发声的物体叫做声源。一切正在发声的物体都在振动,振动停止,发声也停止。固体、液体和气体都能发声,都可以是声源。
①钢琴是靠琴弦的振动发声的;
②笛子是靠空气柱振动发声的;
③哺乳动物是靠声带振动发声的;
④蝉靠胸部的两片鼓膜振动发声;
⑤鸟靠鸣膜振动发声;
⑥蟋蟀靠翅膀相互摩擦发声;
⑦蜜蜂、蚊子、苍蝇在飞行时才有声音,是因为它们飞行时翅膀在振动,如图所示。

声音的产生:
概念的理解:
1. 不同发声体的发声部位一般不同。
2. “振动停止,发声停止”不能叙述为“振动停止,声音消失”,因为振动停止,只是不再发声,而原来发出的声音仍存在并继续传播。
转换放大法理解振动发生:
将不易直接观察到的微小现象,通过某种方式把它形象、直观地呈现出来,这种方法叫转换放大法,是我们探究问题经常采用的一种可行的方法。
例如图所示,在探究“声音是由物体振动产生的”实验中,将正在发声的音叉紧靠悬线下的轻质小球,发现小球被多次弹开。这样做是为了( )
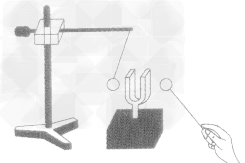
A.使音叉的振动尽快停下来
B.把音叉的微小振动放大,便于观察
C.把声音的振动时间延迟
D.使声波被多次反射形成回声
解析发声体都在振动。音叉的振动幅度很小不易觉察,可用丝线悬吊轻质小球靠近音叉,这样通过轻质小球的跳动,反映出音叉的振动,即把音叉微小的振动放大。
答案B
声现象:知识梳理

正在发声的物体叫做声源。一切正在发声的物体都在振动,振动停止,发声也停止。固体、液体和气体都能发声,都可以是声源。
①钢琴是靠琴弦的振动发声的;
②笛子是靠空气柱振动发声的;
③哺乳动物是靠声带振动发声的;
④蝉靠胸部的两片鼓膜振动发声;
⑤鸟靠鸣膜振动发声;
⑥蟋蟀靠翅膀相互摩擦发声;
⑦蜜蜂、蚊子、苍蝇在飞行时才有声音,是因为它们飞行时翅膀在振动,如图所示。

声音的产生:
| 声音的产生 | 由于物体的振动 |
| 声音的停止 | 振动停止,发生停止 |
| 发声体 | 是一切正在振动的固体,液体,气体 |
| 一切发声体都在振动 | |
概念的理解:
1. 不同发声体的发声部位一般不同。
2. “振动停止,发声停止”不能叙述为“振动停止,声音消失”,因为振动停止,只是不再发声,而原来发出的声音仍存在并继续传播。
转换放大法理解振动发生:
将不易直接观察到的微小现象,通过某种方式把它形象、直观地呈现出来,这种方法叫转换放大法,是我们探究问题经常采用的一种可行的方法。
例如图所示,在探究“声音是由物体振动产生的”实验中,将正在发声的音叉紧靠悬线下的轻质小球,发现小球被多次弹开。这样做是为了( )

A.使音叉的振动尽快停下来
B.把音叉的微小振动放大,便于观察
C.把声音的振动时间延迟
D.使声波被多次反射形成回声
解析发声体都在振动。音叉的振动幅度很小不易觉察,可用丝线悬吊轻质小球靠近音叉,这样通过轻质小球的跳动,反映出音叉的振动,即把音叉微小的振动放大。
答案B
声现象:知识梳理

常见的发声体及发生原因
| 发声体 | 发生原因 |
| 蝉 | 腹基部鼓膜受到振动而发出声音 |
| 机械唱片 | 唱针振动 |
| 人说话 | 声带振动 |
| 打击乐器 | 被打击物体振动 |
| 弦乐器 | 弦的振动 |
| 管乐器 | 管内空气柱振动 |
| 蚊子,苍蝇,密封 | 翅膀振动 |
| 小鸟鸣叫 | 气管和支管交接处的鸣膜振动 |
声速:
在常见物质中的传播速度:
声速与气温的关系:
气温影响空气的密度,气温高,空气的密度小,声波在传播的过程中受到的阻碍小,所以声速较大,因此声音由声源发出后不一定沿直线传播。晴天的中午,地表迅速升温,地表附近的气温比上一层气温高,声音在地表的传播比上层快,于是在地面上发出的声音向四周传播时是向上拐弯的。
| 定义 | 声音存介质中每秒传播的距离叫声速,用v表示 |
| 计算公式 | s=vt,其中 |
| 单位 | 米/秒(m/s),读做米每秒 |
| 常数 | v=340m/s(15℃的空气中) |
| 影响因素 | 介质种类。一般情况下,v固>v液>v气 介质温度。声速随温度的升高而增大,温度每升高1℃,声音在空气中每秒传播的距离增加约0.6m。当空气中不同Ⅸ域的温度有区别时,声音的传播路线是向着低温方向的。如上方的温度低,声音就向上传播,此时,高处的人容易听到低处的声音 |
在常见物质中的传播速度:
| 物质名称 | 传播速度v/m﹒s-1 |
| 空气 | 340 |
| 水 | 1500 |
| 钢铁 | 5200 |
| 松木 | 3320 |
| 玻璃 | 5000-6000 |
声速与气温的关系:
气温影响空气的密度,气温高,空气的密度小,声波在传播的过程中受到的阻碍小,所以声速较大,因此声音由声源发出后不一定沿直线传播。晴天的中午,地表迅速升温,地表附近的气温比上一层气温高,声音在地表的传播比上层快,于是在地面上发出的声音向四周传播时是向上拐弯的。
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比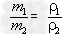 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比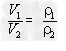 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
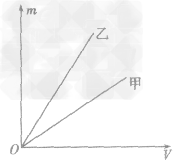
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
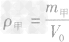 ,ρ乙=
,ρ乙= 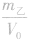 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。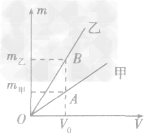
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,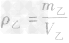
(2)写出该物理量比的表达式:
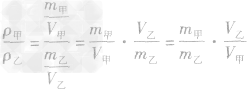
(3)化简:代入已知比值的求解:
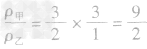
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
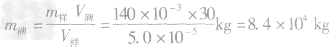 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
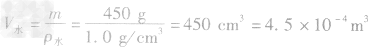 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为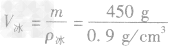 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,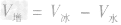 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
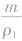 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=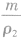 ,合金的体积
,合金的体积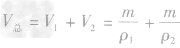 ,则合金的密度
,则合金的密度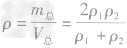
在(2)中两种金属的体积相等,设为
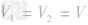 ,合金的体积
,合金的体积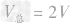 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=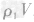 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为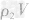 ,合金的质量m总
,合金的质量m总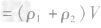 ,合金的密度为
,合金的密度为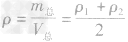 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
发现相似题
与“夏天暴雨前,往往会电闪雷鸣.其中雷声是由于云团之间放电引...”考查相似的试题有:
- 如图所示,将正在发声的音叉紧靠悬挂在线上的小球,会发现小球被_________,这个现象表明__________________________________...
- 下列现象中不能说明声音是怎样发生的现象是( )A.宇航员在月球上要靠无线电话通话B.人说话时手摸喉头、手感觉振动C.正在...
- 以下几个实验现象中,能说明声音产生原因的是A.放在玻璃钟罩内的电铃正在发声,把玻璃钟罩内的空气抽去,铃声明显减弱B.把...
- 将击响的音叉接触水面,会溅起水花,这表明:声音是由于物体的______而产生的,在15℃的空气中声音大约每秒传播______m.
- 下列实验中哪一个不能证明物体振动发声( )A.琴弦的振动B.电动喇叭通电时弹起泡沫小球C.锣面弹起的乒乓球D.对着山谷大叫...
- 进一步探究:液体中的声速与温度有关,关系式为vt=v0+a(t﹣t0),其中:vt表示温度为t时的声速,t0为表格中指出的温度,v0表...
- 某品牌牛奶每盒装有牛奶的质量约为275______(填上合适的单位),体积为0.25______(填上合适的单位),由此可以估算出牛奶的...
- 某工厂要用横截面积为2.5×10-3cm2的铜钱8000cm,应买这种铜线_____g。(已知铜的密度为8.9×103kg/m3)
- 体积是20cm3,质量是89g的空心铜球,在其中空心部分注满水银,则球的总质量是多少?(ρ铜=8.9×103kg/m3,ρ水银=13.6×103kg/m3)
- 质量相等的酒精,硫酸和水,分别装在规格相同的三个试管中,如图所示,试管甲装的是 ______,试管乙装的是 ______.试管丙装...