本试题 “在真空中通电直导线所在的平面内,电子以速度平行导线射出,下图中曲线为电子的可能运动轨迹,其中大致正确的是[ ]A、B、C、D、” 主要考查您对电流的磁场,安培定则
带电粒子在匀强磁场中的运动
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 电流的磁场,安培定则
- 带电粒子在匀强磁场中的运动
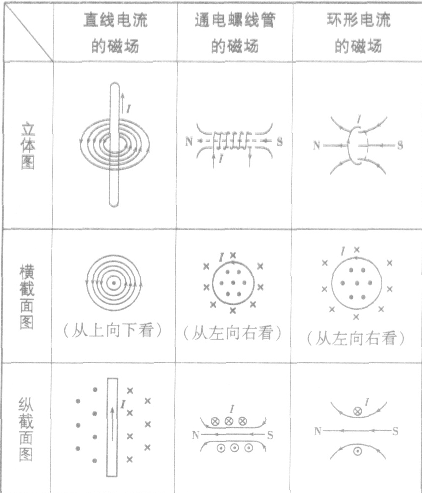


利用安培定则分析电流磁场的方法:
应用安培定则时首先应特别注意伸的是右手,其次注意不同情况下四指环绕方向、大拇指指向的意义不同。
(1)分清“困”和“果”:在判定直线电流的磁场方向时,大拇指指“原因”——电流方向;四指指“结果”——磁场绕向。在判定环形电流的磁场方向时,四指指“原因”——电流绕向;大拇指指“结果”——环内沿中心轴线的磁感线方向指N极。这种方向间的关系也可用一句话概括:“直对直,曲对曲”。在安培定则中大拇指是伸直的,四指是弯曲的。而在电流与磁场的方向中,直线电流中电流是直的,磁感线是弯曲的;环形电流中电流是弯曲的,其中心轴线上磁感线是直线;通电螺线管中电流是弯曲的,内部磁感线是直的,对照相应的安培定则,可知四指与大拇指、电流与相应磁感线问有“直对直,曲对曲”的对应关系。
(2)在直线电流产生的磁场中,要判定横截面某点磁感应强度的方向,切忌与点电荷的电场相混淆。如图所示,要确认甲图中a点场强的方向,需作Q与a的连线,然后由场源电荷的正负确定a点场强是沿连线背离场源电荷还是指向场源电荷;而在乙图中确定点b处的磁场方向时,磁场方向却是与场源电流,与b点连线相垂直的。需先作出,与b点连线及其在b点处的垂线,然后由安培定则确定该点磁场是沿垂线指向顺时针方向还是指向逆时针方向。 
(3)注意等效,优先采用整体法。一个任意形状的闭合电流(如三角形、矩形、圆形) 的磁场,都可以视为若干或无数很短的直线电流磁场叠加而成,从而可以分段进行判定。这种隔离法的判定结果,虽然与视为环形电流的整体法一致,但在步骤上却麻烦多了。
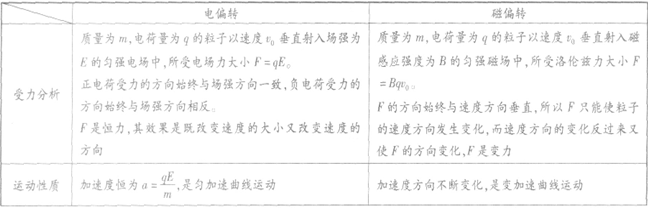
带电粒子在匀强磁场中的运动形式:

电偏转与磁偏转的对比:

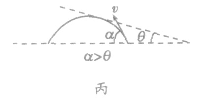
关于角度的两个结论:
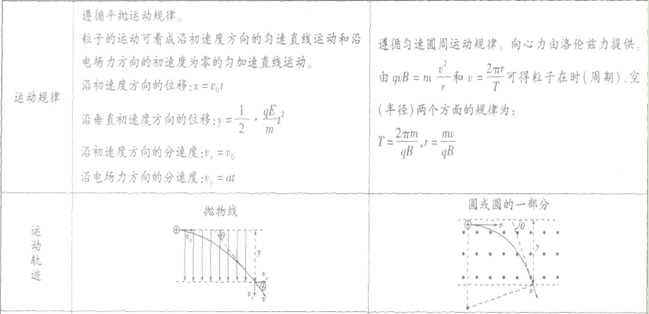
(1)粒子速度的偏向角φ等于圆心角α,并等于AB弦与切线的弦切角θ的2倍(如图所示),即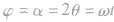 。
。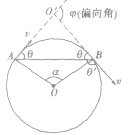
(2)相对的弦切角θ相等,与相邻的弦切角θ'互补,即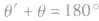
有界磁场中的对称及临界问题:
(1)直线边界
粒子进出磁场时的速度关于磁场边界对称.如图所示。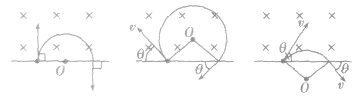
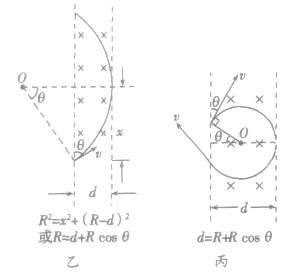
(2)圆形边界
①沿半径方向射入磁场,必沿半径方向射出磁场。
②射入磁场的速度方向与所在半径间夹角等于射出磁场的速度方向与所在半径间的夹角。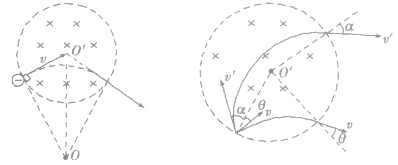
(3)平行边界
存在着临界条件: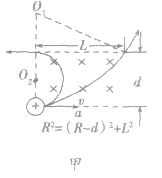
(4)相交直边界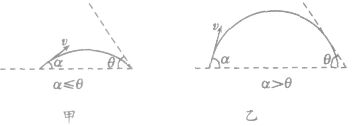
带电粒子在匀强磁场中的匀速圆周运动:


确定轨迹圆心位置的方法:
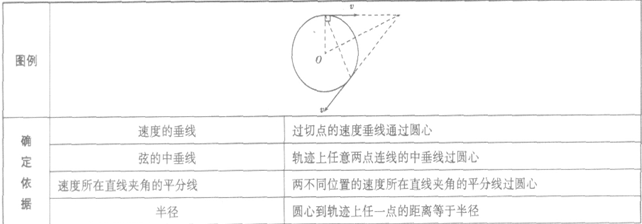
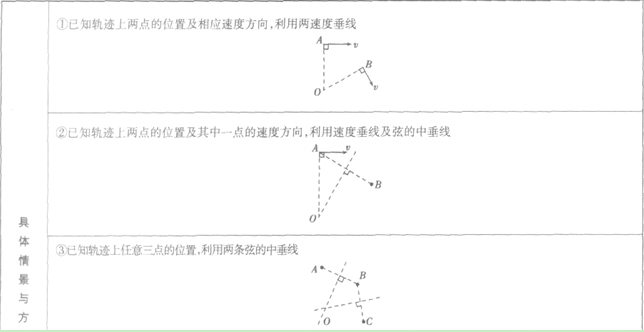
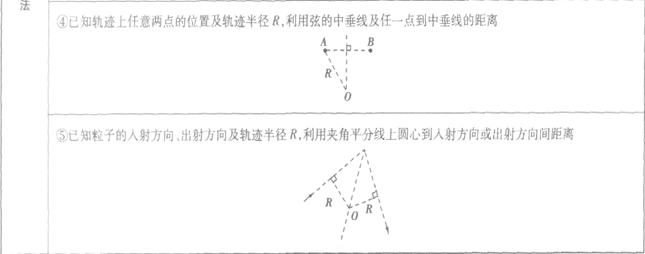
带电粒子在磁场中做圆周运动时间和转过圆心角的求解方法:
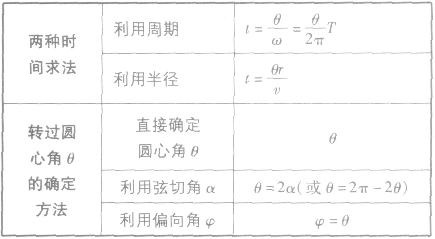
带电粒子在有界磁场中的临界与极值问题的解法:
当某种物理现象变化为另一种物理现象,或物体从一种状态变化为另一种状态时,发生这种质的飞跃的转折态通常称为临界状态,涉及临界状态的物理问题叫做临界问题,产生临界状态的条件叫做临界条件,临界问题能有效地考查学生多方面的能力,在高考题中屡见不鲜。认真分析系统所经历的物理过程,找出与临界状态相对应的临界条件,是解答这类题目的关键,寻找临界条件,方法之一是从最大静摩擦力、极限频率、临界角、临界温度等具有临界含义的物理量及相关规律人手:方法之二是以题目叙述中的一些特殊词语如“恰好”、“刚好”、“最大”、“最高”、“至少”为突破口,挖掘隐含条件,探求临界位置或状态。如:
(1)刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切。据此可以确定速度、磁感应强度、轨迹半径、磁场区域面积等方面的极值。
(2)当速度v一定时,弧长(或弦长)越大,圆周角越大,则带电粒子在有界磁场巾运动的时间越长。(前提条件是弧是劣弧)
(3)当速率v变化时,圆周角大的,运动时间越越长。
“动态圆”问题的解法:
1.入射粒子不同具体地说当入射粒子的比荷不同时,粒子以相同的速度或以相同的动能沿相同的方向射人匀强磁场时,粒子在磁场中运动的周期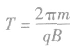 必不相同;运动的轨迹半径
必不相同;运动的轨迹半径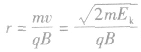 ,在以不同的速度入射时不相同,以相同动能入射时可能不同。
,在以不同的速度入射时不相同,以相同动能入射时可能不同。
2.入射方向不同相同的粒子以相同的速率沿不同方向射人匀强磁场中,粒子在磁场中运动的轨道中,运动周期是相同的,但粒子运动径迹所在空间位置不同,所有粒子经过的空间区域在以入射点为圆心,运动轨迹圆的直径为半径的球形空间内。当磁场空间有界时,粒子在有界磁场内运动的时间不同,所能到达的最远位置不同,从而形成不同的临界状态或极值问题,此类问题中有两点要特别注意:一是旋转方向对运动的影响,二是运动中离入射点的最远距离不超过2R,因R是相同的,进而据此可利用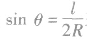 来判定转过的圆心角度、运动时间等极值问题,其中l是最远点到入射点间距离即轨迹上的弦长。
来判定转过的圆心角度、运动时间等极值问题,其中l是最远点到入射点间距离即轨迹上的弦长。
3.入射速率不同
相同的粒子从同一点沿同一方向以不同的速率进入匀强磁场中,虽然不同速率的粒子运动半径不同,但圆心却在同一直线上,各轨迹圆都相切于入射点。在有界磁场中会形成相切、过定点等临界状态,运动时间、空间能到达的范围等极值问题。当粒子穿过通过入射点的直线边界时,粒子的速度方向相同,偏向角相同,运动时间也相同。
4.入射位置不同
相同的粒子以相同的速度从不同的位置射入同一匀强磁场中,粒子在磁场中运动的周期、半径都相同,但在有界磁场中,对应于同一边界上的不同位置,会造成粒子在磁场巾运动的时间不同,通过的路程不同,出射方向不同,从而形成不同的临界状态,小同的极值问题。
5.有界磁场的边界位置变化
相同粒子以相同的速度从同定的位置出发,途经有界磁场Ⅸ域,若磁场位置发生变化时,会引起粒子进入磁场时的入射位置或相对磁场的入射方向发生变化,从而可能引起粒子在磁场中运动时间、偏转角度、出射位置与方向等发生变化,进而形成临界与极值问题。
与“在真空中通电直导线所在的平面内,电子以速度平行导线射出,...”考查相似的试题有:
- 如图所示是几种常见磁场的磁感线分布示意图,下列说法正确的是( )A.图甲中a端是磁铁的S极,b端是磁铁的N极B.图甲中a端是磁...
- 如图所示,a、b、c三枚小磁针分别放在通电螺线管的正上方、右侧和管内,当开关闭合时,且当这些小磁针静止时,小磁针N极的指...
- 竖直导线ab与水平面上放置的圆线圈隔有一小段距离,其中直导线固定,线圈可自由运动,当同时通以如图所示方向的电流时(圆线...
- 如图所示,一金属直杆MN两端接有导线,悬挂于线圈上方,MN与线圈轴线均处于竖直平面内,为使MN垂直纸面向外运动,可以[ ]A....
- 如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸面外,磁感应强度为B。一带正电的粒子以速度v0从O点射...
- 如图所示,左侧为两块长为L=10cm,间距cm的平行金属板,加U=的电压,上板电势高;现从左端沿中心轴线方向入射一个重力不计的...
- 一束带电粒子流以同一方向垂直射入一磁感强度为B的匀强磁场中,在磁场中分成两条轨迹1和2,如图所示,那么它们的速度v、动量P...
- 如图所示,在平面直角坐标系的第二和第三象限区域内有沿y轴负方向的匀强电场,第四象限内存在一水平方向的半径r=m的圆形匀强...
- 对具有相同动能的Q粒子和质子组成的粒子束,有可能把这两种粒子分开的方法是(不计重力)( ) A.使粒子束穿过一匀强电场区...
- 重力不计的带正电的粒子,质量为m,电荷量为q,由静止开始,经加速电场加速后,垂直于磁场方向进入磁感应强度为B的匀强磁场中...