本试题 “阅读材料后回答:材料一:塔底水利水电枢纽工程是2006年浙江省重点建设项目,坝址位于衢江区樟潭镇,见图1(甲);工程建拦河橡胶坝1座,坝长425米,分5跨。...” 主要考查您对液体压强计算公式的应用
压强的大小及其计算
浮力的应用
密度公式的应用
有利于节约能源的措施
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 液体压强计算公式的应用
- 压强的大小及其计算
- 浮力的应用
- 密度公式的应用
- 有利于节约能源的措施
利用液体压强的计算公式计算:ρ、h。
液体压强中隐含“密度不同”的有关计算:
由液体的压强公式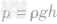 可知,液体的压强大小取决于液体的密度和深度,深度的不同比较直观,一眼可以看到,而密度不同需引起注意,有时直接给出物质不同,密度不同,有时则隐含着密度不同,需要自己发现。
可知,液体的压强大小取决于液体的密度和深度,深度的不同比较直观,一眼可以看到,而密度不同需引起注意,有时直接给出物质不同,密度不同,有时则隐含着密度不同,需要自己发现。
例如图所示,两支相同的试管,内盛等质量的液体,甲管竖直放置,乙管倾斜放置,液体对管底压强的大小关系是()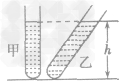
A.p甲<p乙
B.p甲>p乙
C.p甲=p乙
D.上述三种情况都有可能
解析:比较压强就从甲、乙两支试管中液体的密度和深度分析。依据题意已知h相等,因此本题只要比较出甲、乙管中液体的密度ρ,即可判断出正确答案。由质量关系已知,要比较密度很容易想到密度公式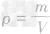 ,从而转向寻找甲、乙两支试管中液体的体积关系,这样问题就得到了解决。由题意可知,两试管液面相平,高度相等,虽然两试管中所装的液体质量相等,但乙管倾斜放置,
,从而转向寻找甲、乙两支试管中液体的体积关系,这样问题就得到了解决。由题意可知,两试管液面相平,高度相等,虽然两试管中所装的液体质量相等,但乙管倾斜放置,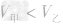 ,所以
,所以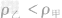 ,据
,据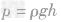 可知
可知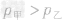 。
。
答案:B
液体对容器底的压力与液体的重力
1.由于液体具有流动性,静止在水平放置的容器中的液体,对容器底的压力不一定等于液体的重力。只有当容器是柱形时,容器底的压力才等于液体的重力:底小口大的容器底受到的压力小于液体的重力;底大口小的容器底受到的压力大于液体的重力。液体对容器底的压力F=pS=ρghS,而Sh的含义是以容器底为底、以液体深度为高的柱体的体积。即V柱=Sh,所以F=pS=ρghS=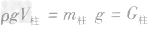 ,G柱的含义为以V柱为体积的那部分液体的重力,如图中阴影部分。即若容器为柱体,则F=G液;若容器为非柱体,则
,G柱的含义为以V柱为体积的那部分液体的重力,如图中阴影部分。即若容器为柱体,则F=G液;若容器为非柱体,则 。
。
2.在盛有液体的容器中,液体对容器底的压力、压强遵循液体的压力、压强规律;而容器对水平桌面的压力、压强遵循固体的压力、压强规律。
例:在水平桌面上放置一空玻璃杯,它的底面积为0.01m2,它对桌面的压强为200Pa。
(1)求玻璃杯的重力。
(2)在玻璃杯中装入1kg水后,水对杯底产,£的压强为900Pa,求水的深度;并通过计算推测出玻璃杯的大致形状是图中甲、乙、丙的哪一种?(水的密度p= 1.0×103k/m3,取g=10N/kg,杯壁的厚度可忽略)
解析:
(1)由 得:玻璃杯的重力:
得:玻璃杯的重力: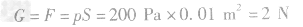
(2)由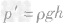 得水的深度:
得水的深度: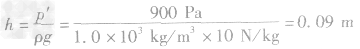
假设杯壁是竖直的,装入1KG水后杯中水的深度应为: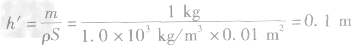 ,因为h'>h,所以水杯底小,口大,大致形状是甲图。
,因为h'>h,所以水杯底小,口大,大致形状是甲图。
液体对容器底的压强、压力与容器对支持面的压强、压力的计算方法:
液体对容器底的压强和压力与容器对支持面的压强和压力不是一同事。
1.液体内部压强是由液体的重力产生的,但液体对容器底的压力并不一定等于液体的重力,而等于底面积所受的压强乘以受力面积,因此,处理液体内部问题时,先求压强再算压力。
2.容器对支持面的压力和压强,可视为固体问题 处理,先分析压力大小,再根据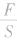 计算压强大小。
计算压强大小。
例:如图所示,一开口的杯子,装上8cm高的水后,放在水平桌面上。已知杯子内部底面积为50cm2,外部底面积为60cm2;杯子装上水后的总质量为 0.6kg,则水对杯底的压力为___N,杯子对桌面的压强为_____Pa.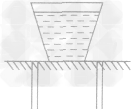
解析:从杯子的形状可知,杯中水对杯底的压力并小等于水的重力,要求液体对容器底的压力时,一般是先求出压强,再根据F=pS求压力,即F=pS=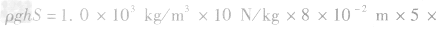 10-3m2=4N,而杯子对桌面的压力为杯与水的总重,即
10-3m2=4N,而杯子对桌面的压力为杯与水的总重,即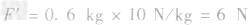 ,压强
,压强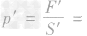
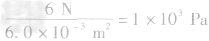 。
。
答案:4N 1×103
P=F/S,式中p单位是:帕斯卡,简称:帕,1帕=1牛/米2,压力F单位是:牛;受力面积S单位是:米2。
对压强公式
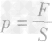 的理解:
的理解:1.此公式适用于任何情况,即固体、液体、气体的压强计算都可用此公式。
2.此公式中各物理量单位分别是p→Pa、F→N、s→m2。在计算物体的压强时,只有当F的单位为N,S 的单位为m2时,压强的单位才能是Pa,因此在计算中必须统一单位。
3.一张报纸平放时对桌子的压强约0.5Pa。成人站立时对地面的压强约为1.5×104Pa,它表示:人站立时,其脚下每平方米面积上,受到脚的压力为1.5× 104N。
4.公式中的,是压力而不是重力。即使在某些情况下,压力在数值上等于物体所受的重力,也不应把公式直接写成
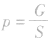 ,而应先注明F=G得:
,而应先注明F=G得: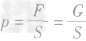 。
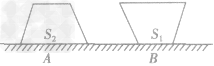
。 5.公式中的受力面积S,是指受力物体发生形变的那部分面积,也就是两物体的实际接触面积,而不一定是受力物体的表面积。如图所示,一个圆台形物体置于水平地面上,分别采用A、B两种方式放置,对地面的压力不变,但图A中受力面积是S2,图B中受力面积为S1,而它们都与水平地面的面积大小无关。
6. 由公式推导出F=pS和
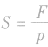 可用于计算压力和受力面积的大小。
可用于计算压力和受力面积的大小。巧用
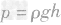 求柱体压强:
求柱体压强:将一密度均匀、高为h的圆柱体放在水平桌面上,桌面受到的压强
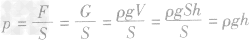 ,所圆柱体(包括长方体、正方体等)产生的压强,只与固体的密度和高度有关,而与固体的重力、体积和底面积因素无关,应用公式
,所圆柱体(包括长方体、正方体等)产生的压强,只与固体的密度和高度有关,而与固体的重力、体积和底面积因素无关,应用公式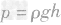 就给解这类题带来很大方便。
就给解这类题带来很大方便。例1如图所示,两圆柱形铁柱的底面半径之比是 3:1,高度相同,则它们对水平地面的压强之比为( )
A.3:1B.1:3C.1:1D.9:l
解析:本题是分析圆柱体的压强,可直接利用公式
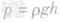 进行分析。因为两圆柱体的密度相同、高度相同,所以压强相同,选项C正确。
进行分析。因为两圆柱体的密度相同、高度相同,所以压强相同,选项C正确。答案:C
浮力的利用:
1.盐水选种我国农民常采用盐水浸泡法来选种,如图,这种方法是把种子放入浓度适宜的盐水中,干瘪、虫蛀的种子密度小于盐水的密度会上浮至液面,而饱满的种子则因为密度大于盐水的密度因此它们会沉在底部。
2.轮船用密度大于水的材料制成能够浮在水面的物体,必须使它能够排开更多的水。根据这个原理,人们制造了轮船,轮船是用密度大于水的钢铁制成的,把它做成空心的,使它的平均密度小于水的密度时,它就会漂浮在水面上,这时船受到的浮力等于自身的重力,所以能浮在水面上。只要船的重力不变,无论船在海里还是河里,它受到的浮力不变。根据阿基米德原理如: G排=ρ液gV排。它在海里和河里浸入水中的体积不同。轮船的大小通常用排水量来表示,排水量就是轮船按设计的要求装满货物即满载时排开水的质量。
3.潜水艇
(1)潜水艇的上浮和下沉是靠压缩空气调节水舱里水的多少来控制自身的重力而实现浮沉的。(如图所示)

(2)浸没在水中的潜水艇排开水的体积,无论下潜多深,始终不变,所以潜水艇所受的浮力始终不变。若要下沉,可充水,使F浮<G。;若要上浮,可排水,使F浮> G。在潜水艇浮出海面的过程中,因为排开水的体积减小,所以浮力逐渐减小,当它在海面上行驶时,受到的浮力大小等于潜水艇的重力。
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比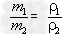 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比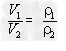 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
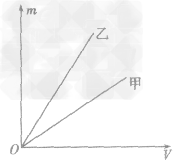
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
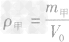 ,ρ乙=
,ρ乙= 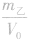 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。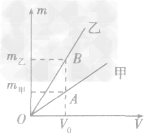
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,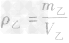
(2)写出该物理量比的表达式:
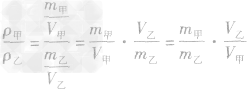
(3)化简:代入已知比值的求解:
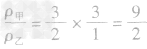
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
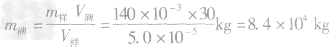 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
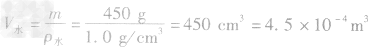 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为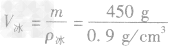 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,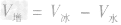 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
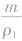 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=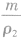 ,合金的体积
,合金的体积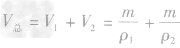 ,则合金的密度
,则合金的密度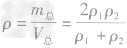
在(2)中两种金属的体积相等,设为
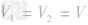 ,合金的体积
,合金的体积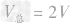 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=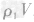 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为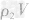 ,合金的质量m总
,合金的质量m总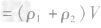 ,合金的密度为
,合金的密度为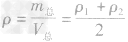 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
一是提高能源的利用率;二是开发和利用新能源,特别是开发和利用太阳能和核能。
具体措施:
(1)节能降耗,从我做起:随手关灯、关电脑等,注意节约用水等等;
(2)注意技术创新,提高能源利用效率,减少废气、废物排放的污染因素;
(3)依靠科学技术创新开发绿色新能源,加强能源利用中的防护措施,提高能源使用的安全性。
能源利用中的效率问题:
1. 热效率: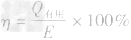 ,Q有用是有效利用的热量,E指总能量。如果是炉子,则E为燃料完全燃烧放出的能量(E=Q总=mq);如果是太阳能热水器,则E 为接收到的太阳能;如果是电热器,则E为电流做功放出的热量。
,Q有用是有效利用的热量,E指总能量。如果是炉子,则E为燃料完全燃烧放出的能量(E=Q总=mq);如果是太阳能热水器,则E 为接收到的太阳能;如果是电热器,则E为电流做功放出的热量。
2. 热机效率: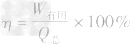 ,其中W有用是指输出的有用功(W有用=Pt),Q总为燃料完全燃烧放出的总能量(Q总=mq)
,其中W有用是指输出的有用功(W有用=Pt),Q总为燃料完全燃烧放出的总能量(Q总=mq)
能源利用的效率问题,关键是分清有效利用的能量和总能量。一般来说,转化成的能量是有效利用的能量,消耗的能量为总能量。
21世纪的能源趋势:
虽然能造是守恒的,但能量转化和转移是有方向的。随着能源消耗的迅速增长,化石能源将会枯竭,必须提高能源的利用率,节约能源,同时不断开发新能源,才能解决能源危机。
与“阅读材料后回答:材料一:塔底水利水电枢纽工程是2006年浙江...”考查相似的试题有:
- 一块长方体砖块,重为10N,侧放于水平桌面上时,它与桌面的接触面积是1×10-2m2,如图所示.它对桌面的压强是______Pa.若沿ab...
- 某同学在家中做测植物油密度的实验时,测得一个平底瓶子质量为0.3kg,瓶内装满水时质量是0.8kg,装满植物油时质量是0.75kg,...
- 如图某索道最高处到最低处全长3000m,上下高度差为600m,吊车与钢索的总接触面积为0.01m2,吊车承载两人后的总重力为2500N....
- 如图所示,A、B是分别盛有适量的煤油和水的相同容器,底面积均为100cm2,置于水平桌面上。现将一实心小球分别放入A、B两容器...
- 牲畜自动饮水器的示意图,如图所示,饮水杯A、B、C的水位可以保持一定,便于牲畜饮用,设计者运用了______原理和______原理.
- 不用天平,用量筒量出 ______mL的酒精,其质量为200g;不用量筒,用天平称出 ______g的煤油,其体积是100mL,并说出用天平测...
- 如图所示,是A、B、C三种物质的质量m与体积V的关系曲线,由图可知,A、B、C三种物质的密度ρA、ρB、ρC和水的密度ρ水之间的关系...
- 三只完全相同的杯子里都装有一些水,把质量相等的实心铅块、铁块和铝块分别放入这三只杯子里,它们都沉没于水中且杯中水面相...
- 近年来,我市的轿车市场十分火爆,各种新型轿车驶进千家万户.如图为某新型轿车测定油箱内油面高度的电路原理图.其中电源电...
- 质量相等半径相同的空心铜球、铁球和铝球各一个(ρ铜>ρ铁>ρ铝),则空心部分体积最大的球是[ ]A.铜球B.铁球C.铝球D.条...