本试题 “登山运动员有时需要使用在两竖直岩石墙间爬上去的技术,如图所示.假定鞋与岩石间的动摩擦因数为0.9,运动员腿长为0.9 m。(1)求运动员可以像图中所示那样站立...” 主要考查您对力的分解
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 力的分解
力的合成与分解:
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
分解方法:
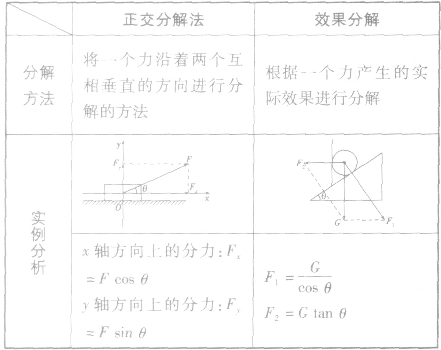
几种按效果分解的实例:


由力的三角形定则求力的最小值:
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值 。
。
(2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值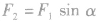 。
。
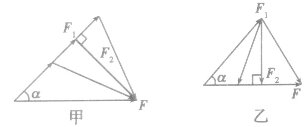
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值 。
。
由圆的切线求力方向的极值:
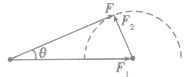
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足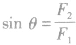 。
。 
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足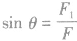 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足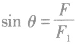 。
。
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
力的分解的几种情况:
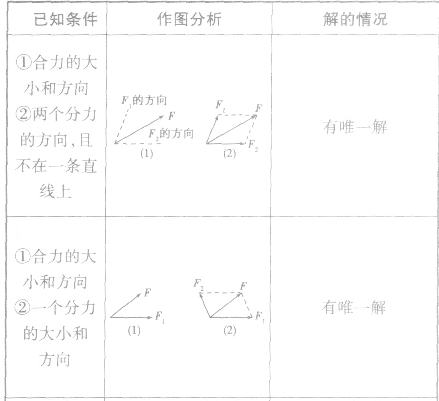
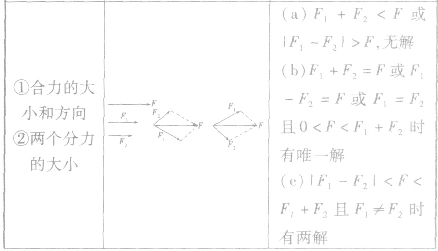
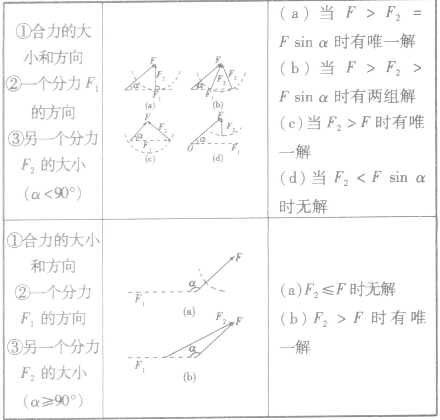
分解方法:

几种按效果分解的实例:


由力的三角形定则求力的最小值:
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值
 。
。 (2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值
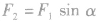 。
。
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值
 。
。由圆的切线求力方向的极值:
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足
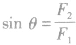 。
。 
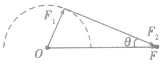
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足
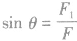 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足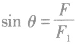 。
。
发现相似题
与“登山运动员有时需要使用在两竖直岩石墙间爬上去的技术,如图...”考查相似的试题有:
- 物理学中存在着许多物理规律,准确地认识物理规律的本质,是学好物理的重要因素之一.如:做匀变速曲线运动的物体,随着时间...
- 如图所示,用绳AC和BC吊起一个物体,绳AC与竖直方向的夹角为60°,绳BC与竖直方向的夹角为30°。若被吊起的物体重100N,试求绳A...
- 在静水中的速度是4m/s,河岸笔直,河宽4m,河水流速为3m/s,以下说法正确的是( )A.船过河的最短时间为0.8sB.船在河中运动...
- 船在静水中的航速是1m/s,河岸笔直,河宽恒定,河水靠近岸边的水流速度为2m/s,河中间的水流速度为3m/s.以下说法中正确的是...
- 某人骑自行车以4m/s的速度向正东方向行驶,天气预报报告当时是正北风,风速为4m/s,则骑车人感觉到风速方向和大小为( )A....
- 如图所示的塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩.在小车A与物体B以相同的水平速度沿吊臂方向...
- 小船在静水中的速度为v,今小船要渡过一河流,渡河时小船朝对岸垂直划行,若船航行至河中心时,水流速度突然增大,则渡河时间...
- 余伯在水库中钓获一尾大头鱼,当鱼线拉着大头鱼在水中向左上方匀速运动时,鱼受到水的作用力方向可能是( )A.水平向左B.水...
- 两个力分别是F1=3N、F2=9N,关于这两个力的合力,下列说法正确的是A.如果这两个力作用于同一个物体上它们的合力可能是15NB....
- 如图所示,两次渡河时船对水的速度大小和方向都不变,已知第第一次实际航程为A至B,位移为S1,实际航速为v1,所用时间为t1....