返回

高中三年级物理

首页
首页 高中三年级物理知识 全反射，临界角 氢原子的能级 试题正文
  • 不定项选择
    氢原子能级图如图所示，若氢原子发出a 、b两种频率的光，在真空中用同一装置做双缝干涉实验，分别得到干涉图样如图甲、乙所示。若a光是氢原子由能级n=5向n=2跃迁时发出的，则关于b光下列说法正确的是

    [     ]

    A．可能是从能级n=4向n=2跃迁时发出的
    B．可能是从能级n=4向n=3跃迁时发出的
    C．a光在水中的传播速度小于b 光在水中的速度
    D．若用a光以α角从玻璃射向空气恰好发生全反射，则b光以同样的入射角从玻璃射向空气也能发生全反射
    本题信息：2011年期末题物理不定项选择难度一般 来源:宗萍
  • 本题答案
    查看答案
本试题 “氢原子能级图如图所示，若氢原子发出a 、b两种频率的光，在真空中用同一装置做双缝干涉实验，分别得到干涉图样如图甲、乙所示。若a光是氢原子由能级n=5向n=2...” 主要考查您对

全反射，临界角

氢原子的能级

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 全反射，临界角
  • 氢原子的能级

光密介质与光疏介质:

1.定义:两种介质相比较，折射率较大的介质叫做光密介质，折射率较小的介质叫做光疏介质
2.特点:
(1)光由光疏介质射人光密介质时，折射角小于入射角；光由光密介质射入光疏介质时，折射角大于入射角。
(2)光在光疏介质中的传播速度大于在光密介质中的传播速度。
(3)光密介质与光疏介质是相对而言的。单独一种介质无法确定它是光密介质还是光疏介质

全反射:

1.定义:光从光密介质射人光疏介质时，折射角大于入射角，当入射角增大到某一角度时，折射角达到90。，折射光完全消失，只剩下反射光，这种现象叫做全反射
2.临界角:
①定义：折射角为90。时的入射角叫做全反射的临界角。
②公式：光由折射率为n的介质射入空气 (真空)时，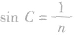
3.条件:
①光由光密介质射向光疏介质
②入射角等于或大于临界角


全反射的计算方法:

光从一种介质射入另一种介质时一般都要同时发生反射与折射现象，如图所示。当光线从光密介质射向光疏介质时，折射角大于入射角。这样就有可能在入射角还没有增大到90。以前，折射角就已经达到90。，以光从水射人空气为例，当入射角增大到某一数值C 时，折射光线恰好掠过水面，和界面平行，折射角等于90。，再继续增大入射角，光线全部反射回水中，不再有折射光线进入空气中，于是形成光的全反射现象。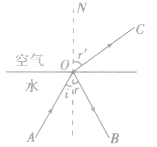

当折射角为90。时的入射角C叫做临界角，可见发生全反射的条件是：
①光线从光密介质射入光疏介质。 
②入射角≥临界角(C)，对于临界角有：。 
分析光的全反射、临界角问题的一般思路：
(1)画出恰好发生全反射的光路。
(2)利用几何知识分析边、角关系，找出临界角。
(3)以刚好发生全反射的光线为比较对象来判断光线是否发生全反射，从而画出其他光线的光路图。


物质的密度与光密介质、光疏介质:

光密介质和光疏介质是相对的，是根据介质对同种频率的光的折射率大小来划分的。折射率较小的称为光疏介质，折射率较大的称为光密介质。显然对同一介质来说，当与其对比的介质不同时，它可能属于光密介质，也可能属于光疏介质，如水相对于空气是光密介质，但相对于玻璃就属于光疏介质了，对于某种介质，没有与之相对比的其他介质时，谈论它是光密介质还是光疏介质是无意义的。而物质的密度与介质的折射率之间没有直接的联系，密度大的介质折射率不一定大，如酒精的密度小于水的密度，但酒精的折射率大于水的折射率。但对于同种物质来说，当其密度变大时，通常折射率也变大。如空气，在海边、靠近海平面的空气温度低，密度大，折射率也大，常引起“海市蜃楼”现象；在沙漠，靠近地面的空气温度高，密度小，折射率也小，这正是引起“沙漠蜃景”的原因。


氢原子的能级:

1、氢原子的能级图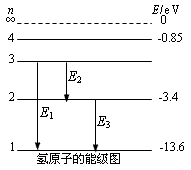

2、光子的发射和吸收
①原子处于基态时最稳定，处于较高能级时会自发地向低能级跃迁，经过一次或几次跃迁到达基态，跃迁时以光子的形式放出能量。
②原子在始末两个能级Em和En（m>n）间跃迁时发射光子的频率为ν，其大小可由下式决定：hυ=Em-En。
③如果原子吸收一定频率的光子，原子得到能量后则从低能级向高能级跃迁。
④原子处于第n能级时，可能观测到的不同波长种类N为：。
⑤原子的能量包括电子的动能和电势能（电势能为电子和原子共有）即：原子的能量En=EKn+EPn。轨道越低，电子的动能越大，但势能更小，原子的能量变小。
电子的动能：，r越小，EK越大。


氢原子的能级及相关物理量:

在氢原子中，电子围绕原子核运动，如将电子的运动看做轨道半径为r的圆周运动，则原子核与电子之间的库仑力提供电子做匀速圆周运动所需的向心力，那么由库仑定律和牛顿第二定律，有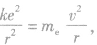，则
①电子运动速率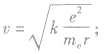
②电子的动能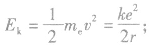
③电子运动周期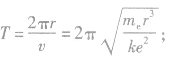
④电子在半径为r的轨道上所具有的电势能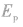
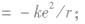
⑤等效电流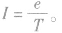由以上各式可见，电子绕核运动的轨道半径越大，电子的运行速率越小，动能越小，电子运动的周期越大．在各轨道上具有的电视能越大。

原子跃迁时光谱线条数的确定方法:

1．直接跃迁与间接跃迁
原子从一种能量状态跃迁到另一种能量状态时，有时可能是直接跃迁，有时可能是间接跃迁，两种情况辐射(或吸收)光子的频率可能不同。
2．一群原子和一个原子
氧原子核外只有一个电子，这个电子在某个时刻只能处在某一个可能的轨道上，在某段时间内，由某一轨道跃迁到另一个轨道时，可能的情况只有一种，但是如果容器中盛有大量的氢原子，这些原子的核外电子跃迁时就会有各种情况出现了。
3．一群氢原子处于量子数为n的激发态时，可能辐射的光谱线条数
如果氢原子处于高能级，对应量子数为n，则就有可能向量子数为(n一1)，(n一2)，(n一3)…1诸能级跃迁，共可形成(n一1)条谱线，而跃迁至量子数为(n一 1)的氢原子又可向(n一2)，(n一3)…1诸能级跃迁，共可形成(n一2)条谱线。同理，还可以形成(n一3)，(n 一4)…1条谱线。将以上分析结果归纳求和，则从量子数为n对应的能级向低能级(n—1)，(n一2)…1跃迁可形成的谱线总条数为(n一1)+(n一2)+(n一3)+ …+1=n(n一1)／2。数学表示为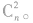
4．一个氢原子处于量子数为n的激发态时，可能辐射的光谱线条数
对于处于量子数为n的一个氢原子，它可能发生直接跃迁，只放出一个光子，也可能先跃迁到某个中间能级上，再跃迁回基态而放出两个光子，也可能逐级跃迁，即先跃迁到n一1能级上，再跃迁到n一2能级上， ……，最后回到基态上，共放出n—1个光子。即一个氢原子在发生能级跃迁时，最少放出一个光子，最多可放出n一1个光子。

利用能量守恒及氢原子能级特征解决跃迁电离等问题的方法:

在原子的跃迁及电离等过程中，总能量仍是守恒的。原子被激发时，原子的始末能级差值等于所吸收的能量，即入射光子的全部能量或者入射粒子的全部或部分能量；原子被电离时，电离能等于原子被电离前所处能级的绝对值，原子所吸收的能量等于原子电离能与电离后电离出的电子的动能之和；辐射时辐射出的光子的能量等于原子的始末能级差。氢原子的能级 F 关系为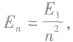，第n能级与量子数n2成反比，导致相邻两能级间的能量差不相等，量子数n越大，相邻能级差越小，且第n能级与第n一1能级的差比第n能级与无穷远处的能级差大，即另外，能级差的大小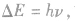故也可利用光子能量来判定能级差大小。


跃迁与电离:

激发的方式:


发现相似题
与“氢原子能级图如图所示，若氢原子发出a 、b两种频率的光，在真...”考查相似的试题有：