本试题 “在月球上以初速度v0竖直上抛一个小球,经过时间t落回到抛出点,已知月球的半径为R,引力常量为G。求:(1)月球的质量;(2)月球的平均密度。” 主要考查您对竖直上抛运动
计算天体质量与密度
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 竖直上抛运动
- 计算天体质量与密度
竖直上抛运动:
将物体以一定初速度沿竖直方向向上抛出,物体只在重力作用下运动(不考虑空气阻力作用),叫做竖直上抛运动。
竖直上抛运动的公式:
vt=v0-gt;h=v0t-![]() gt2;速度位移公式:vt2-v02=-2gh。
gt2;速度位移公式:vt2-v02=-2gh。
运动特征:
①运动到最高点v=0,a=-g(取竖直向下方向为正方向);
②能上升的最大高度hmax=![]() ;
;
③质点在通过同一高度位置时,上升速度与下落速度大小相等;物体在通过一段高度过程中,上升时间与下落时间相等,![]() 。
。
④物体只受重力作用,具有竖直向上的初速度。
运动性质:
初速度不为零的匀变速直线运动。
竖直上抛的处理方法:
1、分段处理法:
①上升阶段:已知v0,a=-g,vt=0的匀减速直线运动,取向上为正方向较方便。所以运动规律为
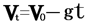 ,
, ,
,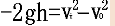
故,上升时间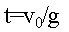 ,最大高度
,最大高度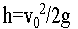 。
。
②最高点v=0,可是不处于静止状态,因为a=g。
③下降阶段:自由落体运动,取向下为正方向较方便。
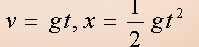
2、对称性:
①竖直上抛的物体上抛达到最大高度与从这一高度落回抛出点所用的时间相等。
②竖直上抛物体在上升和下落过程中经过同一位置时的速度大小相等方向相反。
3、V-t图像:
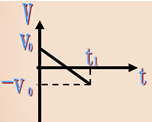
4、整体分析法:
将全过程看成是加速度为-g的匀变速直线运动,应用公式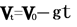 ,
,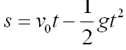
(1)s为正,表示质点在抛出点的上方,s为负表示在抛出点的下方。
(2)由同一s求出的t、可能有两个解,要注意分清其意义。
(3)算出的vt>0表示物体在向上过程中,vt<0表示物体在向下过程中;s>0表示物体在抛出点上方,s<0表示物体在抛出点下方.
计算天体质量与密度:
1、用万有引力定律求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。
2、用万有引力定律计算天体的平均密度:通过观测天体表面运动卫星的周期T,就可以求出天体的密度ρ。
计算天体质量与密度:
1、用万有引力定律求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。以地球的质量的计算为例
①若已知月球绕地球做匀速圆周运动的周期T和半径r,根据: 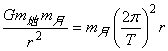 ,得:
,得:![]() ;
;
②若已知月球绕地球做匀速圆周运动的线速度v和半径r,根据: ![]() ,得:
,得:![]() ;
;
③若已知月球绕地球做匀速圆周运动的线速度v和周期T,根据: ![]() 和
和![]() ,得:
,得:![]() ;
;
④若已知地球的半径R和地球表面的重力加速度g,根据: ![]() ,得:
,得:![]() ——此式通常被称为黄金代换式。
——此式通常被称为黄金代换式。
2、用万有引力定律计算天体的平均密度:通过观测天体表面运动卫星的周期T,就可以求出天体的密度ρ。
天体球体积:V=![]() ;天体密度:
;天体密度:![]() (由
(由![]() ,
,![]() ,
,![]() ,r指球体半径,R指轨道半径,当R=r时,
,r指球体半径,R指轨道半径,当R=r时,![]() )。
)。
知识点拨:
科学真是迷人.地球、太阳等天体的质量是多少?天平无法测量.但在我们学习了万有引力定律之后,我们便可以通过它来"称量".求天体质量和密度方法:在地面附近万有引力近似等于物体的重力.由于地球的自转,因而地球表面上的物体随地球自转时需要向心力.所以重力实际上只是万有引力的一个分力,另一个分力就是物体随地球自转时需要的向心力,这个分力与万有引力相比很小忽略不计,可近似认为万有引力等于物体的重力。
与“在月球上以初速度v0竖直上抛一个小球,经过时间t落回到抛出点...”考查相似的试题有:
- 从地面以一定的速度竖直向上抛出一小球,小球从抛出点上升到最高点所用时间为t1,从最高点下落到抛出点所用时间为t2.若空气...
- 如图所示,在一次空地演习中,离地H高 处的飞机以水平速度v1发射一颗炮弹欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度...
- 在高为H处,一小物体由静止开始下落的同时,在其正下方地面上将一石块竖直上抛,发现下落物体和石块在空中相撞时,石块已经开...
- 以35m/s的初速度竖直向上抛出一个小球.不计空气阻力,g取10m/s2.以下判断正确的是( )A.小球到达最大高度时的速度为0B....
- 质量为m的物体以初速υ0做竖直上抛运动.不计空气阻力,从抛出到落回抛出点这段时间内,以下说法正确的是( )A.物体动量变化...
- 小球由地面竖直上抛,上升的最大高度为H,设所受阻力大小恒定,地面为零势能面。在上升至离地高度h处,小球的动能是势能的2倍...
- 以一定的初速度竖直上抛一小球,经过4s回到手中,则抛球的初速度为______ m/s,上升的最大高度为______m(取g=10m/s2)
- 将一物体以速度v从地面竖直上抛,取地面为零势能面,当物体运动到某高度时,它的动能恰为重力势能的一半,不计空气阻力,则这...
- 天文学家新发现了太阳系外的一颗行星。这颗行星的体积是地球的4.7倍,质量是地球的25倍。已知某一近地卫星绕地球运动的周期约...
- 宇航员在火星探测实验室进行实验:测火星表面的重力加速度的值。其中一种方案叫作“对称自由下落”。将真空足够长的直管竖直方...