本试题 “电阻R、电容C和电感器L是常用的电子元器件,在频率为f的交变电流电路中,如图所示,当开关S依次分别接通R、C、L支路,这时通过各支路的电流有效值相等.若将...” 主要考查您对自感现象
电感器对交变电流的作用
电容器对交变电流的作用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 自感现象
- 电感器对交变电流的作用
- 电容器对交变电流的作用
1、自感现象:由于导体本身的电流发生变化而产生的电磁感应现象。
①作用:阻碍原电流的增加,起延迟时间的作用。
②I自的方向:I原是增加的,I自的方向与I原相反;I原是减小的,I自的方向与I原方向相同。
2、自感电动势:在自感现象中产生的感应电动势叫自感电动势。
3、自感系数:L为自感系数,描述线圈产生自感电动势大小本领的物理量。其单位为享,用H表示,1H=103mH=106mH。它的大小是由线圈本身决定,与通不通电流,电流的大小无关。线圈的横截面积越大,线圈越长,匝数越密,它的自感系数就越大。实际上它与线圈上单位长度的匝数n成正比,与线圈的体积成正比。除此外,线圈内有无铁芯起相当大的作用,有铁芯比没有铁芯,自感系数要大得多。
4、自感现象的应用和防止
(1)自感现象的应用——日光灯工作原理
①电路图
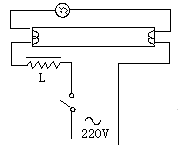
②起动器的作用:利用动触片和静触片的接通与断开起一个自动开关的作用,起动的关键就在于断开的瞬间;
③镇流器的作用:日光灯点燃时,利用自感现象产生瞬时高压;日光灯正常发光时,利用自感现象,对灯管起到降压限流作用。
(2)自感现象的防止:用双线绕法——产生反向电流,使磁场相互抵消。
通电自感和断电自感:


分析自感现象的基本方法:
因为自感现象是以发生自感的那部分电路的电流为主展开的分析,所以在研究自感问题时,应以电流的稳定分布为分析的基点,对电流的变化进行比较后展开分析。一般我们只研究电流从零增大到稳定值和由稳定值减小到零的情况。
1.自感电路中阻碍自感电流变化的原因
(1)当自感电路中电流增大时,增大的电流的能量转化为自感线圈中的磁场能量,而表现出阻碍这种增大的现象。
(2)当自感电路中电流减小时,自感线圈储存的磁场能量会释放出来,转化为电流的能量,而表现出阻碍这种减小的现象。
2.分析自感支路对其他并联支路的影响的步骤
(1)当电源接通,自感电路中电流由零开始增大的瞬时,相当于此电路中电阻突然增大到极大,等效于该支路在瞬时断开。
(2)当电源断开,自感电路中电流减小到零瞬时,此电路的电流会在一段短暂时间内维持原来大小。
(3)通过各支路的电路结构比较它们在稳定状态的电流大小。
(4)把自感线圈当做假想电源,其他支路与新电源的关系确定电路结构,确定电流的分配,再比较各支路新的电流与原来电流的大小关系,分析要处理的问题并得出结论:
3.自感中“闪亮”与“不闪亮”问题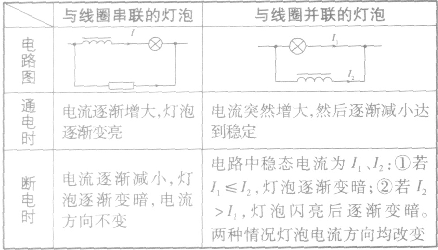
速解自感问题的等效法:
1.通电自感的等效
在通电前线圈中电流为零。通电后线圈中的电流逐渐增大到稳定值。此过程中可将线圈等效为导体,其阻值由无穷大逐渐减小到其直流阻值。然后利用直流动态电路分析中“串反并同”的结论分析通电自感中发生的现象。
2.断电自感的等效
开关断开后,若通电自感线圈中的电流仍能形成通路,则流过自感线圈中的电流将从原来的数值沿原来的方向流动,流动中电流逐渐减小到零。断电的线圈可等效为一个电源,其电动势大小与其外电路有关,与通电线圈中电流有关。E=I(r+R)。当线圈中电流逐渐减小到零时,E逐渐减小到零。
1、感抗:电感对电流的阻碍作用感抗来表示。
2、通直流、阻交流;通低频、阻高频。
电阻、电感器与电容器:
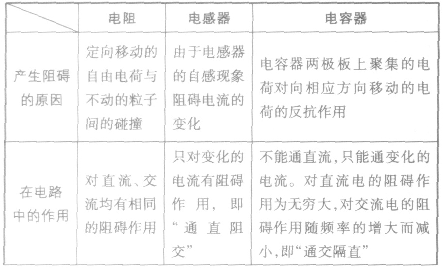
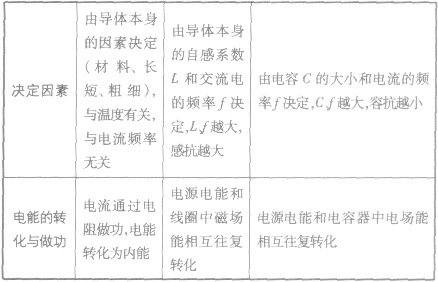
涉及感抗、容抗问题的解法:
电感和电容对交变电流的阻碍作用大小不但与电感、电容本身有关,还跟交流的频率有关。
(1)电感对交变电流的阻碍作用大小用感抗来表示。线圈的自感系数越大,交变电流的频率越高,电感对交变电流的阻碍作用就越大,感抗也越大。电感的作用是“通直流、阻交流,通低频、阻高频”。
(2)电容对交变电流的阻碍作用大小用容抗来表示。电容器的电容越大,交变电流的频率越高,电容对交变电流的阻碍作用就越小,容抗也越小,电容的作用是“通交流、隔直流,通高频、阻低频”。
(3)在分析电流变化时,把感抗、容抗类比于导体的电阻,再用欧姆定律分析。
1、容抗:电容对电流的阻碍作用容抗来表示。
2、通交流、隔直流;通高频、阻低频。
电阻、电感器与电容器:


两种求解交变电流有效值的方法:
交变电流的有效值是根据电流的热效应来规定的,求解交变电流的有效值,通常采用以下两种方法:
(1)若按正(余)弦规律变化的电流,可利用交变电流的有效值与峰值间的关系求解,即: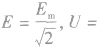 ,U=
,U=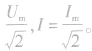
(2)若按非正(余)弦规律变化的电流,可从有效值的定义出发,根据热效应的“三同原则”(同电阻、同时间、同热量)求解,一般选择一个周期内的时间进行计算。
计算交变电流平均值的方法:
交变电流的平均值是指一段时间内交变电流瞬时值的平均值。它表现为交变电流图像中波形与横轴(t轴)所围的“面积”对时间的比值,其值大小与所取时间间隔有关。如正弦式交流电,其正半周期或负半周期内的平均电动势大小为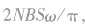 而一个周期内的平均电动势为零。而技术上应用的交变电流的平均值是指一个周期内的交变电流的绝对值的平均值,也等于交变电流在正半个周期或
而一个周期内的平均电动势为零。而技术上应用的交变电流的平均值是指一个周期内的交变电流的绝对值的平均值,也等于交变电流在正半个周期或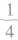 周期内的平均值。
周期内的平均值。
同一交变电流的平均值和有效值并不相同,由于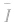
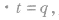 所以交变电流的平均值常用来计算一段时间内通过导线横截面的电荷量。
所以交变电流的平均值常用来计算一段时间内通过导线横截面的电荷量。
平均值不是有效值,也不是初、末瞬时值的平均。
与“电阻R、电容C和电感器L是常用的电子元器件,在频率为f的交变...”考查相似的试题有:
- 如图,A1、A2是两个电流表,R是变阻器,L是带铁芯的线圈,AB和CD两支路直流电阻相同,下列结论正确的有(1).闭合K时,A1示数小...
- 如图所示的电路中,D1和D2是两个相同的小灯泡,L是一个自感系数相当大的线圈,其阻值与R相同.在开关S接通和断开时,灯泡D1和...
- 如图所示的电路中,已知E=20V,R1=20Ω,R2=10Ω,L是纯电感线圈,电源内阻不计,则当S闭合电路稳定时a、b间的电压为多少?在断...
- 如图所示电路中,L是自感系数足够大的线圈,它的电阻可忽略不计,D1和D2是两个完全相同的小灯泡。将电键K闭合,待灯泡亮度稳...
- 如图所示的电路中,L是自感系数很大的线圈,其电阻可忽略不计,A为一灯泡.下列说法正确的是( )A.闭合S时,A灯逐渐变亮B....
- “二分频”音箱内有高、低两个扬声器.音箱要将扩音机送来的含有不同频率的混合音频电流按高、低频段分离出来,送往相应的扬声...
- 某同学在研究电容、电感对恒定电流与交变电流的影响时,采用了如图所示的电路,其中L1、L2是两个完全相同的灯泡,已知把开关置于3、...
- 如图所示电路中,线圈L与灯泡A并联,当合上开关S后灯A正常发光。已知,线圈L的电阻小于灯泡A的电阻。则下列现象可能发生的是A...
- 一理想变压器原、副线圈的匝数之比为11 : 2 ,副线圈的输出电压u随时间变化的规律如图所示,副线圈上仅接入一个阻值为20?? 的...
- 一台收音机的LC调谐电路由电感线圈和可变电容器组成,可变电容器电容的变化范围是30pF到300pF,调谐电路能接收的电磁波的最小...