本试题 “一根两端开口、粗细均匀的长直玻璃管横截面积为S=2×10-3m2,竖直插入水面足够宽广的水中。管中有一个质量为m=0.4kg的密闭活塞,封闭一段长度为L0=66cm的气...” 主要考查您对气体的压强
玻意耳定律(等温定律)
理想气体状态方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 气体的压强
- 玻意耳定律(等温定律)
- 理想气体状态方程
1、温度:宏观上表示物体的冷热程度,微观上是分子平均动能的标志。两种温标的换算关系:T=(t+273)K。绝对零度为-273.15℃,它是低温的极限,只能接近不能达到。
2、气体的体积:气体的体积不是气体分子自身体积的总和,而是指大量气体分子所能达到的整个空间的体积。封闭在容器内的气体,其体积等于容器的容积。
3、气体的压强:气体作用在器壁单位面积上的压力。数值上等于单位时间内器壁单位面积上受到气体分子的总冲量。
①产生原因:大量气体分子无规则运动碰撞器壁,形成对器壁各处均匀的持续的压力。
②决定因素:一定气体的压强大小,微观上决定于分子的运动速率和分子密度;宏观上决定于气体的温度和体积。
玻意耳定律:
1.概念:一定质量的某种气体,在温度不变的条件下其压强与体积变化时的关系,叫做气体的等温变化
2.规律:一定质量的气体,在温度不变的情况下,它的压强跟体积成反比—— 玻意耳定律3.公式: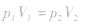
4.图像: 
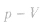 图线为双曲线,同一气体的两条等温线比较,双曲线顶点离坐标原点远的温度高,即
图线为双曲线,同一气体的两条等温线比较,双曲线顶点离坐标原点远的温度高,即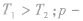
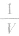 图线为过原点的直线,同一气体比较,斜率(
图线为过原点的直线,同一气体比较,斜率(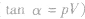 )大的温度高,即
)大的温度高,即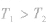 。
。
5.条件:m一定,p不太大,T不太低
6.微观解释:一定质量的理想气体,分子的总数是一定的,在温度保持不变时,分子的平均动能保持不变,气体的体积减小到原来的几分之一,气体的密度就增大到原来的几倍,因此压强就增大到原来的几倍,反之亦然,所以气体的压强与体积成反比。
液柱移动问题的求解方法:
液柱移动问题的分析方法
(1)假设推理法:根据题设条件,假设发生某种特殊的物理现象或物理过程,运用相应的物理规律及有关知识进行严谨的推理,得出正确的答案。巧用假设推理法可以化繁为简,化难为易,简捷解题。
(2)温度不变情况下的液柱移动问题的特点是:在保持温度不变的情况下改变其他题设条件,从而引起封闭气体液柱的移动,或液面的升降,或气体体积的增减。解决这类问题通常假设液柱不移动,或液面不升降,或气体体积不变,然后从假设出发,运用玻意耳定律等有关知识进行推论,求得正确答案。
(3)用液柱或活塞隔开两部分气体,当气体温度变化时,液柱或活塞是否移动?如何移动? 此类问题的特点是:气体的状态参量p、V、T都发生了变化,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解:其一般思路为:
①先假设液柱或活塞不发生移动,两部分气体均做等容变化:
②对两部分气体分别应用查理定律的分比形式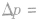
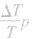 ,求出每部分气体压强的变化量△p,并加以比较。
,求出每部分气体压强的变化量△p,并加以比较。
a.如果液柱两端的横截面积相等,且△p均大于零,意味着两部分气体的压强均增大,则液柱向△p值较小的一方移动;若△p均小于零,意味着两部分气体的压强均减小,则液柱向压强减小量较大的一方(即|△p|较大的一方)移动;若△p相等,则液柱不移动。
b.如果液柱两端的横截面积不相等,则应考虑液柱两端的受力变化(△pS)。,若△p均大于零,则液往向△pS较小的一方移动;若△p均小于零,则液桂向|△pS|值较大的一方移动;若△p等于零,则液柱不移动。
1.表述:一定质量气体的状态变化时,其压强和体积的乘积与热力学温度的比是个常数.
2.表达式:
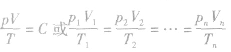
这个常数C由气体的种类与气体的质量决定,或者说这个常数由物质的量决定,与其他参量无关
3.适用条件:质量一定、理想气体
4.与实验定律的关系:
气体的三个实验定律是理想气体状态方程的特例:
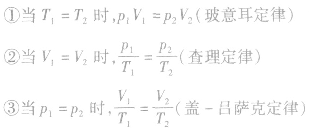
5.两个推论:
(1)密度方程:
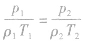
上式与气体的质量无关,即不要求质量恒定
(2)道尔顿分压定律:
一定质量的气体分成n份(或将n份气体合为一份)时
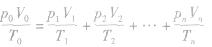
此式要求气体的质量不变,即前后总质量相同
活塞类问题的解法:
1.一般思路
(1)分析题意,确定对象:热学研究对象(一定质量的气体);力学研究对象(活塞、缸体或系统)。
(2)分析物理过程,对热学对象依据气体实验定律列方程;对力学对象依据牛顿运动定律列方程。
(3)挖掘隐含条件,列辅助方程。
(4)联立求解,检验结果。
2.常见类型
(1)系统处于力学的平衡状态,综合利用气体实验定律和平衡方程求解。
(2)系统处于力学的非平衡状态,综合利用气体实验定律和牛顿运动定律求解。
(3)容器与封闭气体相互作用满足守恒定律的条件(如动量守恒、能量守恒、质量守恒等)时,可联立相应的守恒方程求解。
(4)多个相互关联的气缸分别密闭几部分气体时,可分别研究各部分气体,找出它们各自遵循的规律,列出相应的气体状态方程,再列出各部分气体压强之间及体积之问的关系式,联立求解。
变质量气体问题的处理方法:
气体三定律与气体的状态方程都强调“一定质量的某种气体”,即气体状态变化时,气体的质量不能变。用气体三定律与气体状态方程研究变质量气体问题时有多种不同的处理方法。
(1)口袋法:给初状态或者末状态补接一个口袋,把变化的气体用口袋收集起来,从而保证质量不变。
(2)隔离法:对变化部分和不变部分隔离.只对不变部分进行研究,从而实现被研究的气体质量不变。
(3)比较常数法:气体常数与气体质量有关,质量变化,气体常数变化;质量不变,气体常数不变。根据各个状态的已知状态参量计算出各个状态下的气体常数C,然后进行比较。
(4)利用推论法:气体的密度方程不要求质量恒定,可由此得到相应状态的密度,再结合体积等解决问题。也可利用分压定律来研究变质量气体的问题。具体来说,有以下四种典型的情景,可以通过选择适当的对象化变质量为定质量:
①充气问题
向球、轮胎中充气是一个典型的气体变质量问题,只要选择球内原有气体和即将打入的气体作为研究对象,就可把充气过程中的气体质量变化问题转化为定质量气体的状态变化问题。
②抽气问题
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体看成整体来作为研究对象,质量不变,抽气过程中的气体可看成是等温膨胀过程。
③灌气问题
将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题。分析这类问题时,可以把大容器中的气体和多个小容器中的气体看成整体来作为研究对象,将变质量问题转化为定质量问题。
④漏气问题
容器漏气过程中气体的质量不断发生变化,属于变质量问题,不能用理想气体状态方程求解。如果选容器内剩余气体为研究对象,便可使问题变成一定质量的气体状态变化,可用理想气体状态方程求解。
与“一根两端开口、粗细均匀的长直玻璃管横截面积为S=2×10-3m2,...”考查相似的试题有:
- 如图为竖直放置的粗细均匀的密闭细管,水银柱将气体分隔成A、B两部分,初始温度相同.使A、B升高相同温度达到稳定后,体积变...
- 用隔板将一绝热容器隔成A和B两部分,A中盛有一定质量的理想气体,B为真空,如图甲.现把隔板抽去,A中的气体自动充满整个容器...
- 对于一定量的理想气体,下列说法正确的是 ( ) A.若气体的压强和体积都不变,其内能也一定不变 B.若气体的内能不变,其状...
- 如图所示,两根玻璃管a和b开口向下固定在水槽中,玻璃管内被水各封有一定质量的气体.平衡时,a管内的水面低于水槽中的水面,...
- 如图所示,一根竖直的弹簧支持着一倒立气缸的活塞,使气缸悬空而静止。设活塞与缸壁间无摩擦,可以在缸内自由移动,缸壁导热...
- 一定质量的理想气体,从图示A状态开始,经历了B、C,最后到D状态,下列判断中正确的是( ) A.A→B温度升高,压强不变 B.B→C...
- 如图所示,一个开口向上的圆筒气缸直立于地面上,距缸底2L处固定一个中心开孔的隔板a,在小孔处装有一个能向下开启的单向阀门...
- 一圆筒形真空容器,在筒顶系着的轻弹簧下挂一质量不计的活塞,弹簧处于自然长度时,活塞正好触及筒底,如图所示,当在活塞下...
- 一定质量的理想气体处于某一平衡状态,此时压强为P0,有人设计了四种途径,使气体经过每种途径后压强仍为P0,这四种途径是①先...
- 气体温度计结构如图所示.玻璃测温泡A内充有理想气体,通过细玻璃管B和水银压强计相连.开始时A处于冰水混合物中,左管C中水...