本试题 “关于热现象和热学规律,下列说法中正确的是( ) A.只要知道气体的摩尔体积和阿伏伽德罗常数,就可以算出气体分子的质量 B.第二类永动机不可能制成是因为它...” 主要考查您对阿伏伽德罗常数
能量守恒定律、第一类永动机
理想气体状态方程
液体的表面张力
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 阿伏伽德罗常数
- 能量守恒定律、第一类永动机
- 理想气体状态方程
- 液体的表面张力
阿伏加德罗常量:
摩尔的任何物质含有的微粒数都相同,这个数的测量值NA=6.02×1023 mol-1。是联系微观世界和宏观世界的桥梁。它把物质的摩尔质量、摩尔体积这些宏观物理量和分子质量、分子体积这些微观物理量联系起来了。
能量守恒定律:
1.内容:能量既不能凭空产生,也不能凭空消失,它只能从一种形式转化为另一种形式,或者从一个物体转移到另一个物体,在转化或转移的过程中,能的总量保持不变
2.能量形式的多样性:物体运动具有机械能、分子运动具有内能、电荷具有电能、原子核内部的运动具有原子能等等,可见,在自然界中不同形式的能量与不同形式的运动相对应
3.不同形式的能量间转化:“摩擦生热”是通过克服摩擦力做功将机械能转化为内能;水壶中的水沸腾时水蒸气对壶盖做功将壶盖顶起,表明内能转化为机械能;电流通过电热丝做功可将电能转化为内能等等。这些实例说明了不同形式的能量之间可以相互转化,且这一转化过程是通过做功来完成的
4.意义:
①能的转化与守恒是分析解决问题的一个极为重要的方法,它比机械能守恒定律更普遍。例如物体在空中下落受到阻力时,物体的机械能不守恒,但包括内能在内的总能量是守恒的。
②能量守恒定律是19世纪自然科学中三大发现之一,也庄严宣告了第一类永动机幻想的彻底破灭。
③能量守恒定律是认识自然、改造自然的有力武器,这个定律将广泛的自然科学技术领域联系起来
5.第一类永动机:
不消耗任何能量却能源源不断地对外做功的机器。
第一类永动机不可能存在,因为它违背了能量守恒定律
1.表述:一定质量气体的状态变化时,其压强和体积的乘积与热力学温度的比是个常数.
2.表达式:
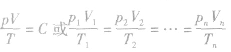
这个常数C由气体的种类与气体的质量决定,或者说这个常数由物质的量决定,与其他参量无关
3.适用条件:质量一定、理想气体
4.与实验定律的关系:
气体的三个实验定律是理想气体状态方程的特例:
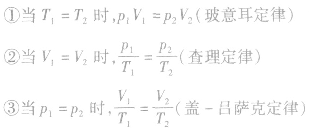
5.两个推论:
(1)密度方程:
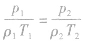
上式与气体的质量无关,即不要求质量恒定
(2)道尔顿分压定律:
一定质量的气体分成n份(或将n份气体合为一份)时
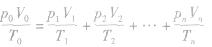
此式要求气体的质量不变,即前后总质量相同
活塞类问题的解法:
1.一般思路
(1)分析题意,确定对象:热学研究对象(一定质量的气体);力学研究对象(活塞、缸体或系统)。
(2)分析物理过程,对热学对象依据气体实验定律列方程;对力学对象依据牛顿运动定律列方程。
(3)挖掘隐含条件,列辅助方程。
(4)联立求解,检验结果。
2.常见类型
(1)系统处于力学的平衡状态,综合利用气体实验定律和平衡方程求解。
(2)系统处于力学的非平衡状态,综合利用气体实验定律和牛顿运动定律求解。
(3)容器与封闭气体相互作用满足守恒定律的条件(如动量守恒、能量守恒、质量守恒等)时,可联立相应的守恒方程求解。
(4)多个相互关联的气缸分别密闭几部分气体时,可分别研究各部分气体,找出它们各自遵循的规律,列出相应的气体状态方程,再列出各部分气体压强之间及体积之问的关系式,联立求解。
变质量气体问题的处理方法:
气体三定律与气体的状态方程都强调“一定质量的某种气体”,即气体状态变化时,气体的质量不能变。用气体三定律与气体状态方程研究变质量气体问题时有多种不同的处理方法。
(1)口袋法:给初状态或者末状态补接一个口袋,把变化的气体用口袋收集起来,从而保证质量不变。
(2)隔离法:对变化部分和不变部分隔离.只对不变部分进行研究,从而实现被研究的气体质量不变。
(3)比较常数法:气体常数与气体质量有关,质量变化,气体常数变化;质量不变,气体常数不变。根据各个状态的已知状态参量计算出各个状态下的气体常数C,然后进行比较。
(4)利用推论法:气体的密度方程不要求质量恒定,可由此得到相应状态的密度,再结合体积等解决问题。也可利用分压定律来研究变质量气体的问题。具体来说,有以下四种典型的情景,可以通过选择适当的对象化变质量为定质量:
①充气问题
向球、轮胎中充气是一个典型的气体变质量问题,只要选择球内原有气体和即将打入的气体作为研究对象,就可把充气过程中的气体质量变化问题转化为定质量气体的状态变化问题。
②抽气问题
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体看成整体来作为研究对象,质量不变,抽气过程中的气体可看成是等温膨胀过程。
③灌气问题
将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题。分析这类问题时,可以把大容器中的气体和多个小容器中的气体看成整体来作为研究对象,将变质量问题转化为定质量问题。
④漏气问题
容器漏气过程中气体的质量不断发生变化,属于变质量问题,不能用理想气体状态方程求解。如果选容器内剩余气体为研究对象,便可使问题变成一定质量的气体状态变化,可用理想气体状态方程求解。
如果在液体表面任意画一条线(如图所示),线两侧的液体之间的作用力是引力,它的作用是使液体表面绷紧,所以叫做液体的表面张力
成因:表面层内分子分布比较稀疏,分子间距大,分子力表现为引力
与“关于热现象和热学规律,下列说法中正确的是( ) A.只要知道...”考查相似的试题有:
- 已知铜的摩尔质量为6.35×10-2kg·mol-1,密度为8.9×103kg/m3,阿伏加德罗常数为6×1023mol-1,试估 算铜原子的直径。
- 在“用油膜法估测分子大小”的实验中,所用的油酸酒精溶液的浓度为每1000 mL溶液中有纯油酸0.6 mL,用注射器测得l mL上述溶液有...
- 下列说法中正确的是 ( ) A.要知道气体的摩尔体积和阿伏加德罗常数,就可以算出气体分子的体积 B.悬浮在液体中的微粒足够...
- 如图甲所示,一轻弹簧的两端与质量分别为mA和mB的两物块A、B相连接,并静止在光滑的水平面上,已知mA=1kg.现使A瞬时获得水平...
- 下列说法正确的是( ) A.随着科技的发展,永动机是可以制成的 B.太阳照射到地球上的光能转化成了其他形式的能量,但照射到...
- 不定项选择下列说法正确的是( )A.第一类永动机不可能制成是因为它违反了能量守恒定律B.第二类永动机不可能制成是因为它违...
- 第一类永动机是不可能制成的,这是因为第一类永动机( ) A.不符合机械能守恒定律 B.违背了能的转化和守恒定律 C.没有合理...
- 如图,水平放置的汽缸内壁光滑,一个不导热的活塞将汽缸内的气体分为A、B两部分,两部分气体可以分别通过放在其中的电热丝加...
- 一根两端开口、横截面积为S=2cm2足够长的玻璃管竖直插入水银槽中并固定(插入水银槽中的部分足够深)。管中有一个质量不计的...
- 容积为20L的钢瓶内,贮有压强为1.5×107Pa的氧气。打开钢瓶的阀门,让氧气分装到容积为5L的氧气袋中(袋都是真空的),充气后的...