本试题 “一皮球从0.8m高处落到地面,然后反弹能跳起到离地0.45m高处,若球与地面接触的时间为0.1s,则在与地面接触时,球的平均加速度大小为______m/s2,方向为______...” 主要考查您对加速度
匀变速直线运动的速度与时间的关系
机械能守恒定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 加速度
- 匀变速直线运动的速度与时间的关系
- 机械能守恒定律
定义:
在匀变速直线运动中,速度的变化量Δv跟发生这个变化所用时间Δt的比值,叫做匀变速直线运动的加速度,用a表示。加速度即速度的变化率。
物理意义:
加速度是表示速度变化的快慢与改变方向的物理量。
公式: ,加速度的国际制单位是米每二次方秒,符号m/s2。
,加速度的国际制单位是米每二次方秒,符号m/s2。
方向:
与速度变化Δv的方向一致,但不一定与v的方向一致,从加速度的产生上来说,加速度的方向与合外力的方向相同。
方法与知识感悟:
加速度、速度与速度变化率的区别和理解:
①加速度是描述速度变化快慢的物理量,不是描述速度大小的物理量,所以与速度的大小没有必然联系
②加速度实质是由物体的受力和物体的质量决定的.从运动学的角度来看,加速度由速度的变化与变化所用时间的比值来量度,说明加速度不是仅仅由速度的变化决定的;
③加速度的方向与速度的方向没有必然联系,但与速度变化的方向一致,其实质是与物体所受到的合外力方向一致.
④加速度即速度的变化率.速度的变化量大,速度的变化率不一定大,速度达最大时,速度的变化率可为零。
例:
在变速直线运动中,下面关于速度和加速度关系的说法,正确的是( )
A.加速度与速度无必然联系
B.速度减小时,加速度也一定减小
C.速度为零时,加速度也一定为零
D.速度增大时,加速度也一定增大
答案:A
匀变速直线运动:
物体在一条直线上运动,如果在相等的时间内速度的变化相等,这种运动就叫做匀变速直线运动。也可定义为:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动。
匀变速直线运动的速度公式:
Vt=V0+at。
公式说明:
- 速度公式是匀变速直线运动速度的一般表示形式。它所表明瞬时速度与时刻t的对应关系。
- 通常取初速度v0方向为正方向,加速度a可正可负(正、负表示方向),在匀变速直线运动中a恒定。
①当a与v0同方向时,a>0表明物体的速度随时间均匀增加,如下左图。
②当a与v0反方向时,a<0表明物体的速度随时间均匀减少,如下右图。
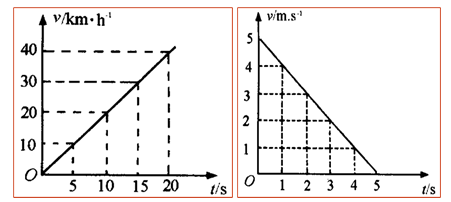
3. 速度图象是对速度公式的直观体现.图象斜率表示加速度,图象与时间轴所围的面积表示位移。
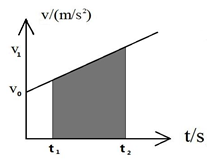
1、内容:只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变。
2、表达式:
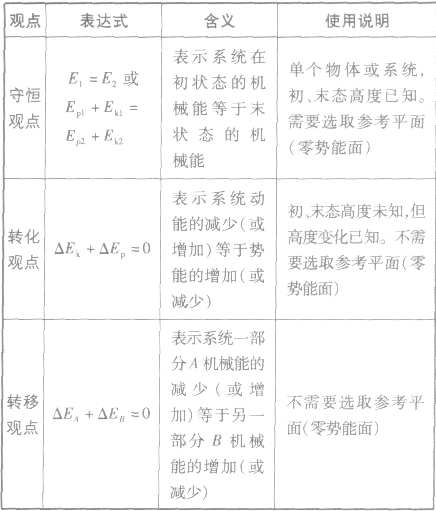
3.条件
机械能守恒的条件是:只有重力或弹力做功。可以从以下三个方面理解:
(1)只受重力作用,例如在不考虑空气阻力的情况下的各种抛体运动,物体的机械能守恒。
(2)受其他力,但其他力不做功,只有重力或弹力做功。例如物体沿光滑的曲面下滑,受重力、曲面的支持力的作用,但曲面的支持力不做功,物体的机械能守恒。
(3)其他力做功,但做功的代数和为零。
判定机械能守恒的方法:
(1)条件分析法:应用系统机械能守恒的条件进行分析。分析物体或系统的受力情况(包括内力和外力),明确各力做功的情况,若对物体或系统只有重力 (或弹力)做功,没有其他力做功或其他力做功的代数和为零,则系统的机械能守恒。
(2)能量转化分析法:从能量转化的角度进行分析:若只有系统内物体间动能和重力势能及弹性势能的相互转化,系统跟外界没有发生机械能的传递,机械能也没有转化成其他形式的能(如内能),则系统的机械能守恒。
(3)增减情况分析法:直接从机械能的各种形式的能量的增减情况进行分析。若系统的动能与势能均增加或均减少,则系统的机械能不守恒;若系统的动能不变,而势能发生了变化,或系统的势能不变,而动能发生了变化,则系统的机械能不守恒;若系统内各个物体的机械能均增加或均减少,则系统的机械能不守恒。
(4)对一些绳子突然绷紧、物体间非弹性碰撞等,除非题目特别说明,否则机械能必定不守恒。
竖直平面内圆周运动与机械能守恒问题的解法:
在自然界中,违背能量守恒的过程肯定是不能够发生的,而不违背能量守恒的过程也不一定能够发生,因为一个过程的进行要受到多种因素的制约,能量守恒只是这个过程发生的一个必要条件。如在竖直平面内的变速圆周运动模型中,无支撑物的情况下,物体要到达圆周的最高点,从能量角度来看,要求物体在最低点动能不小于最高点与最低点的重力势能差值。但只满足此条件物体并不一定能沿圆弧轨道运动到圆弧最高点。因为在沿圆弧轨道运动时还需满足动力学条件:所需向心力不小于重力,由此可以推知,在物体从圆弧轨道最低点开始运动时,若在动能全部转化为重力势能时所能上升的高度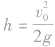 满足
满足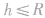 时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在
时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在 ,物体上升到圆周最高点时的速度
,物体上升到圆周最高点时的速度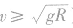 )时,物体可做完整的圆周运动;若在
)时,物体可做完整的圆周运动;若在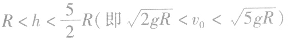 时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度
时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度 满足
满足 。故在解决这类问题时不能单从能量守恒的角度来考虑。
。故在解决这类问题时不能单从能量守恒的角度来考虑。
与“一皮球从0.8m高处落到地面,然后反弹能跳起到离地0.45m高处,...”考查相似的试题有:
- 下列关于速度和加速度的说法中,正确的是A.加速度表示速度变化的大小B.物体的速度为零,加速度也一定为零C.运动物体的加速...
- 短跑运动员起跑时的好坏,对于是否能取得好成绩十分关键。如图所示,当发令枪响时必须奋力蹬地,发挥自己的最大体能,以获取...
- 甲车以10m/s,乙车以4m/s的速率在同一直车道中同向前进,若甲车驾驶员在其前方3m处发现乙车,立即刹车使甲车匀减速运动,为使...
- 卡车原来用10m/s的速度在平直公路上匀速行驶,因为道口出现红灯,司机从较远的地方开始刹车,使卡车匀减速前进,当车减速到2 ...
- 竖直向上抛出一个物体,由于受到空气阻力作用,物体落回抛出点的速率小于抛出时的速率,则在这过程中( )A.物体的机械能守...
- 如图所示,倾斜轨道AC与有缺口的圆轨道BCD相切于C,圆轨道半径为R,两轨道在同一竖直平面内,D是圆轨道的最高点,缺口DB所对...
- 在游乐节目中,选手需借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论。如图所示,他们将选手简化为质...
- 如图所示:小强把质量为0.5kg的石块从10m高处以30°角斜向上方抛出,初速度是v0=5m/s.小强通过定量计算得出了石块落地时的速...
- 在竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环轨道上做圆周运动,如图所示,到达最高点C时的速率是vC...
- 如图所示,在长度一定的细线下方系一小球,线的另一端固定,使悬线与竖直方向成不同偏角θ(0°<θ≤90°)时无速释放。则小球摆...