本试题 “如图所示,矩形单匝导线框abcd竖直放置,其下方有一磁感应强度为B的有界匀强磁场区域,该区域的上边界PP'水平,并与线框的ab边平行,磁场方向与线框平面垂直...” 主要考查您对功
磁场对通电导线的作用:安培力、左手定则
导体切割磁感线时的感应电动势
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 功
- 磁场对通电导线的作用:安培力、左手定则
- 导体切割磁感线时的感应电动势
功:
1、功的定义:力和作用在力的方向上通过的位移的乘积。是描述力对空间积累效应的物理量,是过程量。
2、功的两个必要因素:作用在物体上的力;物体在力的方向上发生的位移。
3、功的定义式:W=Fscosα,其中F是恒力,s是作用点的位移,α是力与位移间的夹角(功的单位焦耳,简称焦,符号J)。
4、功的计算
①恒力的功可根据W=FScosα进行计算,本公式只适用于恒力做功;
②根据W=P·t,计算一段时间内平均做功;
③利用动能定理计算力的功,特别是变力所做的功;
④根据功是能量转化的量度反过来可求功。
力做功情况的判定方法:
一个力对物体做不做功,是做正功还是做负功,判断的方法是:
(1)看力与位移之间的夹角,或者看力与速度之间的夹角:为锐角时,力对物体做正功;为钝角时,力对物体做负功;为直角时,力对物体不做功。
(2)看物体间是否有能量转化:若有能量转化,则必定有力做功。此方法常用于相连的物体做曲线运动的情况。
变力做功的求法:
公式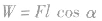 只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
1.用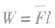 求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用
求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用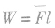 求变力F所做的功。其平均值大小 为
求变力F所做的功。其平均值大小 为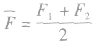 ,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
2.用微元法(或分段法)求变力做功变力做功时,可将整个过程分为几个微小的阶段,使力在每个阶段内不变,求出每个阶段内外力所做的功,然后再求和。当力的大小不变而方向始终与运动方向间的夹角恒定时,变力所做的功形: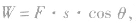 其中s是路程。
其中s是路程。
3.用等效法求变力做功若某一变力做的功等效于某一恒力做的功,则可以应用公式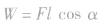 来求。这样,变力做功问题就转化为了恒力做功问题。
来求。这样,变力做功问题就转化为了恒力做功问题。
4.用图像法求变力做功存F—l图像中,图线与两坐标轴所围“面积”的代数和表示F做的功,“面积”有正负,在l轴上方的“面积”为正,在l轴下方的“面积”为负。
5.应用动能定理求变力做功
如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能变化量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
6.利用功能关系求变力做功
在变力做功的过程中,当有重力势能、弹性势能以及其他形式的能量参与转化时,可以考虑用功能关系求解。因为做功的过程就是能量转化的过程,并且转化过程中能量守恒。
7.利用W=Pt求变力做功
这是一种等效代换的观点,用W=Pt计算功时,必须满足变力的功率是恒定的。若功率P是变化的,则需用 计算,其中当P随时间均匀变化时,
计算,其中当P随时间均匀变化时, 。
。
安培力与洛伦兹力:
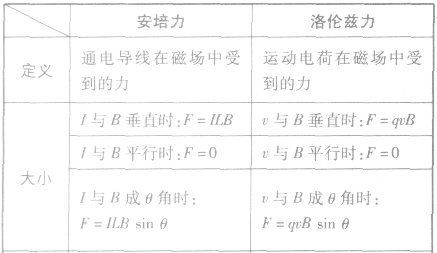

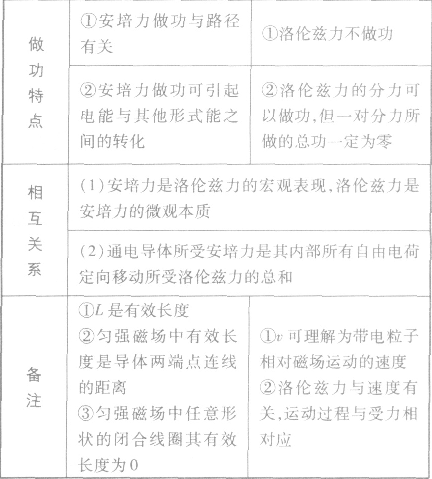
通电导线在安培力作用下运动方向的判定方法:
要判定通电导线在安培力作用下的运动,首先必须清楚导线所在位置磁场的分布情况,然后才能结合左手定则准确判定导线的受力情况,进而确定导线的运动方向。常用的方法如下: 1.电流元法
(1)同一磁场中的弯曲导线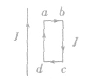
把整段弯曲导线分为多段直线电流元,先用左手定则判定每段电流元受力的方向,然后判定整段导线所受合力的方向,从而确定导线的运动方向,如在图中,要判定导线框abcd的受力可将其分为四段来判定,若将导线框换作导线环时,可将其分为多段直线电流元。
(2)不同磁场区域中的直线电流当直导线处于不同的磁场区域中时,可根据导线本身所处的物理情景,将导线适当分段处理,如图甲中,要判定可自由运动的通电直导线AB在蹄形磁铁作用下的运动情况时,以蹄形磁铁的中轴线OO’为界,直导线在OO’两侧所处的磁场截然不同,则可将AB以OO’为分界点分为左右两段来判定。 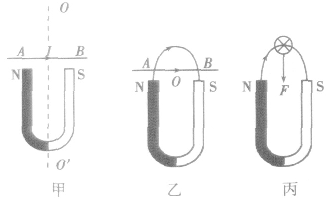
2.特殊位置法因电流所受安培力的方向是垂直于电流和磁场所决定的平面的,虽然电流与磁场之间夹角不同时电流所受安培力大小不同,但所受安培力的方向是不变的 (要求电流从平行于磁场的位置转过的角度不超过 180。)。故可通过转动通电导线到某个便于分析的特殊位置,然后判定其所受安培力的方向,从而确定其运动方向。如在上图甲中,初始位置磁场在平行于电流方向上的分量对电流无作用力,但一旦离开初始位置,此磁场分量就会对电流产生作用力,如上图乙所示。但此分量对电流在转动过程中作用力的方向不方便判定.可将此导线转过90。,此时电流方向与该磁场分量方向垂直,用左手定则很容易判定出受力方向,如上图丙所示,
3.等效法
(1)从磁体或电流角度等效
环形电流可以等效成小磁针,通电螺线管可以等效成条形磁铁或多个环形电流,反过来等效也成立。将环形电流与小磁针相互等效时,它们的位置关系可以认为是小磁针位于环形电流的中心处,N、S极连线与环面垂直,且N、S极与电流方向遵从安培定则。如在图中,两通电圆环同心,所在平面垂直,要判定可自南转动的圆环,I2的运动情况,可将其等效为一小磁针。 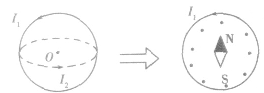
(2)从磁感线分布情况的角度等效
根据要判定的电流或磁体所在处的磁感线分布,将其所在处的磁场等效为某一能够在该处产生类似磁场的场源电流或磁体,然后再用电流之间或磁体之间相互作用的规律来判定。如在图中,导线AB所在处的磁感线分布与位于其下方与纸面垂直的通电直导线在该处产生的磁感线类似(注意是类似而不是相同),所以可以将蹄形磁铁等效为一通电直导线进而进行判定。 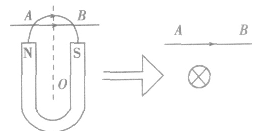
4.结论法
当两电流之间或两等效电流之间发生相互作用时,可利用电流之间相互作用的规律直接判定,只是同前所述,此法应慎用。
(1)两平行直线电流在相互作用过程中,无转动趋势,同向电流互相吸引,反向电流互相排斥;
(2)两不平行的直线电流互相作用时,有转到平行且电流方向相同的趋势。
5.转换研究对象法
定性分析磁体在电流磁场作用下如何运动的问题,可先分析电流在磁体磁场中所受的安培力,然后由牛顿第三定律,确定磁体所受电流磁场的作用力,从而确定磁体所受的合力及运动方向。如在图中要判定磁铁所受电流的作用力,可以分析磁铁对电流的作用力。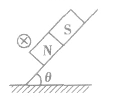
安培力作用下力学问题的解决方法:
由于安培力的方向总是垂直于电流方向与磁场方向决定的平面,即F一定垂直于B和I,但B和I不一定垂直。因此涉及安培力的问题常呈现于三维空间中,要解决这类问题,需从合适的方位将立体图改画为二维平面图,再通过受力分析及运动情况分析,结合平衡条件或牛顿运动定律解题。
导体切割磁感线产生的电动势:
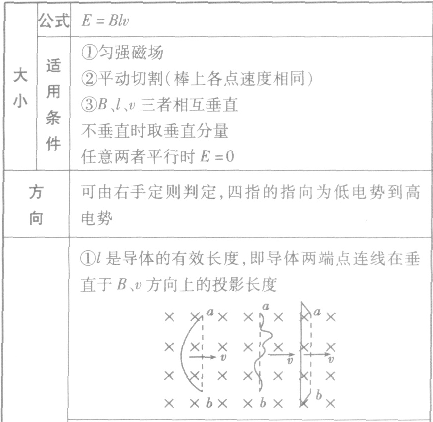
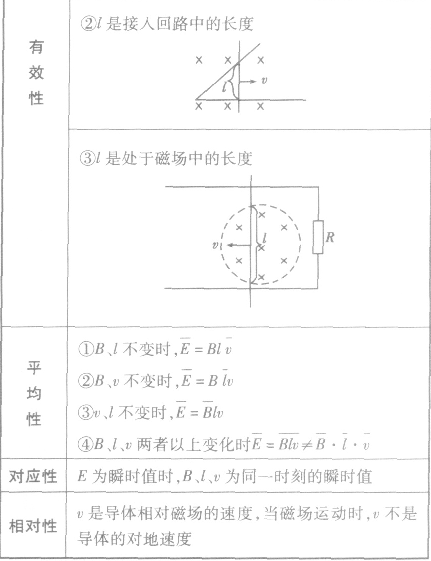
电磁感应中电路问题的解法:
电磁感应规律与闭合电路欧姆定律相结合的问题,主要涉及电路的分析与计算。解此类问题的基本思路是:
(1)找电源:哪部分电路产生了电磁感应现象,则这部分电路就是电源。
(2)由法拉第电磁感应定律求出感应电动势的大小,根据楞次定律或右手定则确定出电源的正负极。
①在外电路,电流从正极流向负极;在内电路,电流从负极流向正极。
②存在双感应电动势的问题中,要求出总的电动势。
(3)正确分析电路的结构,画出等效电路图。
①内电路:“切割”磁感线的导体和磁通量发生变化的线圈都相当于“电源”,该部分导体的电阻相当于内电阻。
②外电路:除“电源”以外的电路即外电路。
(4)运用闭合电路欧姆定律、串并联电路特点、电功率等列方程求解。
与“如图所示,矩形单匝导线框abcd竖直放置,其下方有一磁感应强...”考查相似的试题有:
- 质量为1kg的质点静止于光滑水平面上,从t=0时起,第1秒内受到2N的水平外力作用,第2秒内受到同方向的1N的外力作用.下列判断...
- 通电矩形导线框abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab边与NM平行.关于MN的磁场对线框的作用,下列叙...
- 如图,两根互相平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、o、b在M、N的连线...
- 两绝缘导体环、大小相同,环面垂直,环中通有相同大小的恒定电流,如图所示,则圆心处磁感应强度的方向为( )(面水平,面垂直...
- 如图所示,两根足够长的固定平行金属光滑导轨位于同一水平面,导轨上横放着两根相同的导体棒ab、cd与导轨构成矩形回路.导体...
- 如图所示,等腰直角三角形区域内分布有垂直于纸面向外的匀强磁场,它的底边在x轴上且长为L,高为L。纸面内一边长为L的正方形...
- 质量为0.1g的小球带5×10-4C电量的负电荷,套在一根足够长的绝缘杆上,杆与水平方向成370角,球与杆间的摩擦系数μ=0.40,置于B...
- 把一根长L = 10cm的导线垂直磁感线方向放入如图所示的匀强磁场中,当导线中通以I1= 2A的电流时,导线受到的安培力大小为1.0×1...
- 两根平行光滑金属导轨MN和PQ水平放置,其间距为d=0.6m,磁感应强度为B=0.5T的匀强磁场垂直轨道平面向下,两导轨之间连接的电...
- 如图,用电阻为1Ω的硬导线做成一边长为1m的方框.方框置于绝缘粗糙水平面内,其右半部位于一匀强磁场中,磁感应强度方向垂直...