（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即，k是一个对所有行星都相同的常,高中三年级,物理试题,开普勒行星运动定律考点,计算天体质量与密度考点,好技网

计算题
（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即，k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量k的表达式。已知引力常量为G，太阳的质量为M_太。
（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立。经测定月地距离为3.84×10⁸m，月球绕地球运动的周期为2.36×10⁶S，试计算地球的质量M_地。（，结果保留一位有效数字）

本题信息：2012年专项题物理计算题难度较难来源:周永伏（高中物理）
本题答案
查看答案

本试题 “（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即，k是一个对所有行星都相同的常量。将行星...” 主要考查您对
开普勒行星运动定律

计算天体质量与密度
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

开普勒行星运动定律
计算天体质量与密度

开普勒行星运动定律：

1、所有行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上。
2、对每个行星而言太阳和行星的连线在相等的时间内扫过相同的面积。
3、所有行星轨道的半长轴R的三次方与公转周期T的二次方的比值都相同，即常量。
4、常用开普勒三定律来分析行星在近日点和远日点运动速率的大小。

开普勒三定律的对比：

开普勒第一定律：
开普勒第一定律，也称轨道定律：每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点。

开普勒第二定律:
开普勒第二定律，也称面积定律：在相等时间内，太阳和运动中的行星的连线（向量半径）所扫过的面积都是相等的。这一定律实际揭示了行星绕太阳公转的角动量守恒。（角动量在高中学习中不考查）

开普勒第三定律:
开普勒第三定律，也称周期定律：是指绕以太阳为焦点的椭圆轨道运行的所有行星，其椭圆轨道半长轴的立方与周期的平方之比是一个常量。

知识点拨：
近年高考试题中的天体运动问题，试题情境熟悉，多为匀速圆周运动模型，不是卫星环绕地球的圆周运动，就是行星环绕太阳的圆周运动。运算简单，大多数试题直接运用开普勒第三定律进行分析或计算，有些试题则需运用牛顿第二定律与万有引力定律、“黄金代换”等分析计算。

计算天体质量与密度：

1、用万有引力定律求天体的质量：通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R，就可以求出天体的质量M。
2、用万有引力定律计算天体的平均密度：通过观测天体表面运动卫星的周期T，就可以求出天体的密度ρ。

计算天体质量与密度：

1、用万有引力定律求天体的质量：通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R，就可以求出天体的质量M。以地球的质量的计算为例
①若已知月球绕地球做匀速圆周运动的周期T和半径r，根据：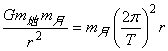
，得：；
②若已知月球绕地球做匀速圆周运动的线速度v和半径r，根据：
，得：；
③若已知月球绕地球做匀速圆周运动的线速度v和周期T，根据：
和，得：；
④若已知地球的半径R和地球表面的重力加速度g，根据：
，得：——此式通常被称为黄金代换式。
2、用万有引力定律计算天体的平均密度：通过观测天体表面运动卫星的周期T，就可以求出天体的密度ρ。
天体球体积：V=；天体密度：（由，，，r指球体半径，R指轨道半径，当R=r时，）。

知识点拨：
科学真是迷人.地球、太阳等天体的质量是多少?天平无法测量.但在我们学习了万有引力定律之后,我们便可以通过它来"称量".求天体质量和密度方法：在地面附近万有引力近似等于物体的重力.由于地球的自转,因而地球表面上的物体随地球自转时需要向心力.所以重力实际上只是万有引力的一个分力,另一个分力就是物体随地球自转时需要的向心力,这个分力与万有引力相比很小忽略不计,可近似认为万有引力等于物体的重力。

发现相似题

与“（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道...”考查相似的试题有：