本试题 “长度L=0.4m的细线,拴着一个质量m=0.4kg的小球,在竖直平面内作圆周运动,小球运动到最低点时离地面高度h=0.8m,此时细线受到的拉力F=13N,g取10m/s2,求:(...” 主要考查您对平抛运动
线速度
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 平抛运动
- 线速度
平抛运动的定义:
将物体以一定的初速度沿水平方向抛出,不考虑空气阻力,物体只在重力作用下所做的运动,叫做平抛运动。
平抛运动的特性:
以抛出点为坐标原点,水平初速度V0,竖直向下的方向为y轴正方向,建立如图所示的坐标系,在该坐标系下,对任一时刻t: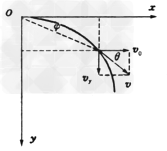
①位移
分位移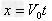 (水平方向),
(水平方向),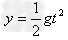 (竖直方向);
(竖直方向);
合位移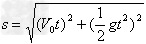 ,
, (φ为合位移与x轴夹角)。
(φ为合位移与x轴夹角)。
②速度
分速度 (水平方向),Vy=gt(竖直方向);
(水平方向),Vy=gt(竖直方向);
合速度 ,
,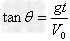 (θ为合速度V与x轴夹角)。
(θ为合速度V与x轴夹角)。
③平抛运动时间: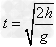 (取决于竖直下落的高度)。
(取决于竖直下落的高度)。
④水平射程: (取决于竖直下落的高度和初速度)。
(取决于竖直下落的高度和初速度)。
类平抛运动:
(1)定义当物体所受的合外力恒定且与初速度垂直时,物体做类平抛运动。
(2)类平抛运动的分解方法
①常规分解法:将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力的方向)的匀加速直线运动,两分运动彼此独立,互不影响,且与合运动具有等时性。
②特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为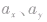 ,,初速度
,,初速度 分解为
分解为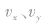 ,然后分别在x、y方向上列方程求解。
,然后分别在x、y方向上列方程求解。
(3)类平抛运动问题的求解思路
根据物体受力特点和运动特点判断该问题属于类平抛运动问题——求出物体运动的加速度——根据具体问题选择用常规分解法还是特殊分解法求解。
(4)类抛体运动
当物体在巨力作用下运动时,若物体的初速度不为零且与外力不在一条直线上,物体所做的运动就是类抛体运动。
在类抛体运动中可采用正交分解法处理问题,基本思路为:
①建立直角坐标系,将外力、初速度沿这两个方向分解。
②求出这两个方向上的加速度、初速度。
③确定这两个方向上的分运动性质,选择合适的方程求解。
线速度的定义:
质点沿圆周运动通过的弧长与所用时间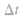 的比值叫做线速度。
的比值叫做线速度。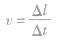 ,
,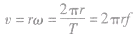 。
。
线速度的特性:
线速度是矢量,方向和半径垂直,和圆周相切。它是描述做圆周运动的物理运动快慢的物理量。
对线速度的理解:
物体上任一点对定轴作圆周运动时的速度称为“线速度”。它的一般定义是质点作曲线运动时所具有的顺时速度。它的方向沿运动轨道的切线方向,故又称切向速度。它是描述作曲线运动的质点运动快慢和方向的物理量。物体上各点作曲线运动时所具有的顺时速度,其方向沿运动轨道的切线方向。 (高中物理中的切线方向就指速度一侧的方向,和数学中的切线不同)
知识点拨:
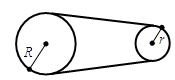
如图,大圆和小圆有同一根皮带相连,皮带上的各个点的速率相同,所以大圆和小圆圆周上的线速度是相同的。
与“长度L=0.4m的细线,拴着一个质量m=0.4kg的小球,在竖直平面内...”考查相似的试题有:
- 在不计空气阻力的情况下,下列说法中正确的是( )A.从同一高度,以大小不同的速度同时水平抛出两个物体,它们一定同时着地...
- 如图所示,从倾角为θ的足够长的斜面上的A点,先后将同一小球以不同的初速度水平向右抛出,第一次初速度为v1,球落到斜面上前...
- 如图所示,在同一竖直方向,小球a、b从高度不同的两点分别以初速度va和vb沿水平方向抛出,经过时间ta和tb后落到与两抛出点水...
- (1)一跳水运动员从离水面10m 高的平台上向上跃起,举双臂直体离开台面,此时其重心位于从手到脚全长的中点,跃起后重心升高...
- 在地面上方的真空室内,有一对平行金属板M、N竖直放置,两板间存在恒定的电势差,设两板间的电场可看作是匀强电场,且两板外...
- 一个物体以v0的初速度作平抛运动,在某时刻物体的竖直分位移与水平分位移的比值为k,则根据以上条件可求出的量是( )A.从抛...
- 为了清理堵塞河道的冰凌,空军实施投弹爆破。飞机在河道上空高H处以速度v0水平匀速飞行,投掷下炸弹并击中目标求炸弹刚脱离飞...
- 两个小球固定在一根长为L 的细杆的两端,绕杆上的O 点做圆周运动,如图所示,当小球A 的速度为v1,小球B 的速度为v2时,则转...
- 用细线拴住一个小球在光滑的水平面内做匀速圆周运动,下列描述小球运动的物理量,发生变化的是A.动能B.线速度C.周期D.角速度
- 如图所示,传送带装置保持2m/s的速度顺时针转动,现将一质量m=0.5kg 的物体从离皮带很近的a点,轻轻的放上,设物体与皮带间的...