平衡状态:

物体保持静止或匀速直线运动的状态称为平衡状态。静止状态称为静平衡，匀速直线运动状态称为动平衡。
①对静止的理解静止与速度v=0不是一回事，物体保持静止状态，说明a=0,a=0，两者同时成立，若仅是v=0，a≠0，如上抛到最高点的物体，此时物体并不能保持静止，上抛到最高点的物体并非处于平衡状态。
②力学中，当物体缓慢移动时，往往认为物体处于平衡状态。
③“静止”与“匀速直线运动”看起来好像是两种不同的运动形式，但本质却相同，这是因为物体的初始运动状态不同，若初始状态物体是静止的，则物体会一直静止着；若初始状态是做匀速直线运动的，则物体必然会保持匀速直线运动的状态。

力的平衡:

作用在物体上的几个力的合力为零，这种情况叫做力的平衡。

平衡条件：

1．内容为了使物体保持平衡状态，作用在物体上的力必须满足的条件，即平衡条件。
2．共点力平衡条件物体在共点力作用下处于平衡状态的条件是所受合外力为零，即。
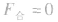相互作用力与一对平衡力的对比：

解决平衡问题的常用方法：

 1．合成法与分解法这两种方法常用在物体在三个力作用下处于平衡状态的问题：
合成法：将三个力中的任意两个力合成为一个力，则其合力与第三个力平衡，把三力平衡问题转化为二力平衡问题。
分解法：当物体受到三个共点力的作用处于平衡状态时，利用平行四边形对任意一个力沿另外两个力的作用线方向分解，则这两个分力分别与另外两个力等大反向。
无论是利用合成法还是利用分解法，都需要在作出平行四边形后再利用图中几何关系来解三角形，从而求出力的大小或方向，常用到的数学知识有：
(1)三角函数定义当出现直角三角形时，可利用三角函数的定义来求解力的大小或方向：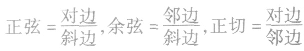

(2)正弦定理对于任意三角形，都有对边与对角的正弦比值相等，如图：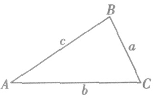


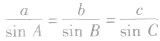
(3)相似三角形当力的三角形与图中的几何三角形相似时，仍有对应边成比例的关系。如在图所示的装置中，各力之间满足下列关系：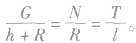
 

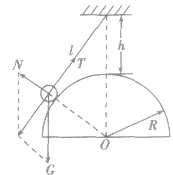
(4)菱形的性质当有两个力大小相等时，求这两个力的合力或将第三个力分解，就会得到一个菱形。而菱形的对角线相互垂直平分，而且平分一组对角。如在处理涉及滑轮或光滑挂钩的平衡问题时，将滑轮或光滑挂钩两侧绳上的拉力合成，运算过程就相对简便。
(5)余弦定理有时还需用到余弦定理，如在图中，有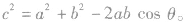

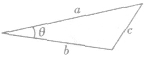
2．矢量三角形法物体在三个力作用下处于平衡状态时，这三个力必可构成一封闭三角形。通过受力分析，画出物体受力示意图，将力平移后组成三角形。然后直接利用上面所述的数学知识解三角形。
3．正交分解法当物体受到多个共点力的作用处于平衡状态时，可以利用正交分解法建立坐标系，则有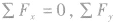=0。通常根据平衡条件，应用正交分解法解题，在解决多个力平衡的问题时尤为方便。但是使用时应注意根据具体情况选择合适的坐标系，一般应遵循的原则为：不在坐标轴上的力越少越好，各力与坐标轴之间的夹角是特殊角为好。
4．整体法和隔离法以上几种方法的着眼点是物体受力情况，而整体法和隔离法是针对研究对象而言的，是解决连接体问题时需考虑的方法。
(1)整体法：它是把两个或两个以上的物体组成的系统作为一个整体来研究的一种分析方法，当只研究系统而不涉及系统内部的相互作用时一般可采用整体法。
(2)隔离法：它是将研究对象从周围物体(连接体)中隔离出来进行分析的方法。一般在研究系统内物体间相互作用时采用隔离法。

动态平衡问题的解决方法：

动态问题包括动态平衡问题的分析和动态非平衡问题的分析。
所谓动态平衡问题是指通过控制某些物理量，使物体的状态发生缓慢变化，而在这个过程中物体又始终处于一系列的平衡状态中。
解动态平衡问题通常有两种方法：
1．图解法
对研究对象在状态变化过程中的若干状态进行受力分析，依据某一参量的变化，在同一图中作出物体在若干状态下力的平衡图(力的三角形或平行四边形)，再由动态力的平行四边形各边长度变化及角度变化确定力的大小及方向的变化情况。
图解法通常使用在三力作用下或可等效为三力作用下的动态平衡问题。
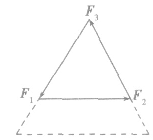
(1)三个力的方向都不变。如图所示，此种情况下任一力增大时，其余两力也增大，反之亦然。
 
(2)三个力中有一个力恒定，有一个力方向恒定。如图所示，此情况下可作出力的矢量三角形(或平行四边形)，确定三角形中不变的边与方位不变的边，由线段长度及另一边的方位变化来确定力的大小、方向变化情况。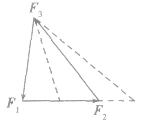

2．解析法
对物体进行受力分析后，利用平衡条件列出方程，解出所判断量的表达式，利用有关数学知识讨论表达式得出答案。从物体受力数量来说，解析法与图解法不同。解析法不仅可以用来解决三个力作用下的动态平衡问题，并且对多个力作用下的动态平衡问题用解析法更方便。从解析法需引入的变量来看，可以是某一角度(这通常需要在力的三角形巾有一个角是不变的)，也可以是某一线段的长度(这种情况下通常题目中出现的几何三角形与力的三角形相似)，这是在三力作用下物体处于动态平衡。若是多个力作用下的动态平衡，通常以某一角度为变量，利用正交分解来获得平衡方程，进而得到要分析的物理量的表达式。
3．动态平衡中的滑轮模型对于轻质光滑动滑轮及与之作用相当的光滑挂钩、光滑环等，具有如下特征：
(1)两侧绳中张力相同；
(2)两侧绳与竖直方向夹角相等；
(3)绳与竖直方向的夹角θ取决于绳的总长度l及两悬点问水平距离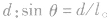

平衡物体的临界与极值问题的解决方法:

1．临界与极值问题
(1)临界问题某种物理现象变化为另一种物理现象或物体从某种特性变化为另一种特性时，发生质的飞跃的转折状态为临界状态，临界状态也可理解为“恰好出现”或“恰好不出现”某种现象的状态。平衡物体的临界状态是指物体所处平衡状态将要变化的状态，是物体所处的平衡状态将要被破坏而尚未被破坏的状态。涉及临界状态的问题叫临界问题。解决这类问题一定要注意 “恰好出现”或“恰好不出现”的条件。
(2)极值问题极值是指研究平衡问题中某物理量变化时出现的最大值或最小值。中学物理的极值问题可分为简单极值问题和条件极值问题，区分的依据就是是否受附加条件限制，如受附加条件限制，则为条件极值。
2．解决方法
(1)临界问题的解决方法解决临界问题的基本思维方法是假设推理法，即先假定物体处于某一状态，然后根据平衡条件及相关知识列方程求解，再根据求得的结果反过来推断物体在给定条件下应处的状态。
(2)极值问题的解决方法对于简单极值问题，可先对物体进行受力分析，然后由平衡条件列出方程，再明确题目中的物理量在什么条件下取极值，或在出现极值时有何物理特征，根据这些条件或特征去寻找极值。对于条件极值问题，有如下两种解决方法：
①解析法：根据物体的平衡条件列方程，在解方程时采用数学知识求极值。通常用到的数学知识有二次函数求极值，均值定理求极值，讨论分式求极值，三角函数求极值以及几何法求极值等。
②图解法：根据物体的平衡条件作出力的矢量图，如只受三个力时，则这三个力必构成封闭矢量三角形，然后根据矢量图进行动态分析，确定最大值和最小值，此法简便、直观。

作用力和反作用力：

力是物体对物体的作用，两个物体之间的作用总是相互的，任何物体是施力物体的同时也是受力物体，两个物体问相互作用的这一对力，叫做作用力和反作用力。
相互作用的一对力，可任选其中一个力称为作用力，则另一个力就是反作用力。即把相互作用的两个力哪个称为作用力或反作用力并不是绝对的，其中一个力叫作用力，另一个力就叫反作用力。