本试题 “若a，b，c∈R+，且a+b+c=1，则的最小值是（ ）。” 主要考查您对三个正数的算术-几何平均不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 三个正数的算术-几何平均不等式
定理：
如果a，b，c∈R，那么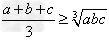
，当且仅当a=b=c时，等号成立；
推广：
对于n个正数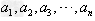
，它们的算术平均不小于它们的几何平均，即
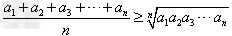，（当且仅当
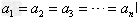时，等号成立）。
三个正数的算术、几何平均数不等式求最值：
设x,y,z都是正数，则有：
(1)若xyz=S（定值），则当x=y=z时，x+y+z有最小值，最小值为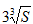
。
(2)若x+y+z=P（定值），则当x=y=z时，xyz有最大值，最大值为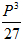
。
注：一正、二定、三等。
发现相似题
与“若a，b，c∈R+，且a+b+c=1，则的最小值是（ ）。”考查相似的试题有：