本试题 “如图所示在竖直平面内建立直角坐标系XOY,OY表示竖直向上的方向.已知该平面内存在沿OX轴负方向的区域足够大的匀强电场,现有一个带电量为2.5×10-7C、质量为1...” 主要考查您对竖直上抛运动
电场强度的定义式
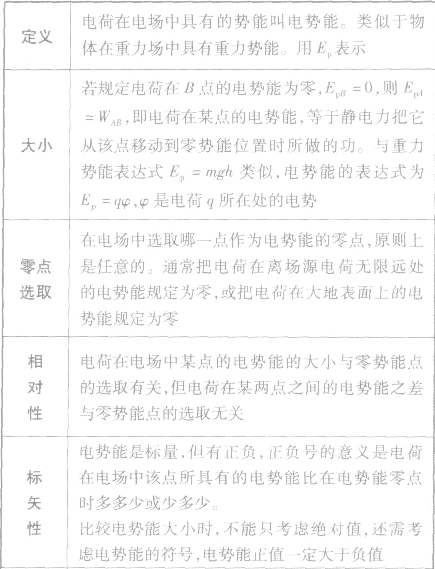
电势能
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 竖直上抛运动
- 电场强度的定义式
- 电势能
竖直上抛运动:
将物体以一定初速度沿竖直方向向上抛出,物体只在重力作用下运动(不考虑空气阻力作用),叫做竖直上抛运动。
竖直上抛运动的公式:
vt=v0-gt;h=v0t-![]() gt2;速度位移公式:vt2-v02=-2gh。
gt2;速度位移公式:vt2-v02=-2gh。
运动特征:
①运动到最高点v=0,a=-g(取竖直向下方向为正方向);
②能上升的最大高度hmax=![]() ;
;
③质点在通过同一高度位置时,上升速度与下落速度大小相等;物体在通过一段高度过程中,上升时间与下落时间相等,![]() 。
。
④物体只受重力作用,具有竖直向上的初速度。
运动性质:
初速度不为零的匀变速直线运动。
竖直上抛的处理方法:
1、分段处理法:
①上升阶段:已知v0,a=-g,vt=0的匀减速直线运动,取向上为正方向较方便。所以运动规律为
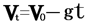 ,
, ,
,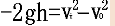
故,上升时间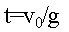 ,最大高度
,最大高度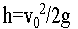 。
。
②最高点v=0,可是不处于静止状态,因为a=g。
③下降阶段:自由落体运动,取向下为正方向较方便。
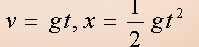
2、对称性:
①竖直上抛的物体上抛达到最大高度与从这一高度落回抛出点所用的时间相等。
②竖直上抛物体在上升和下落过程中经过同一位置时的速度大小相等方向相反。
3、V-t图像:
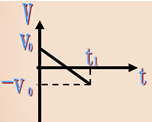
4、整体分析法:
将全过程看成是加速度为-g的匀变速直线运动,应用公式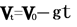 ,
,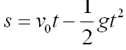
(1)s为正,表示质点在抛出点的上方,s为负表示在抛出点的下方。
(2)由同一s求出的t、可能有两个解,要注意分清其意义。
(3)算出的vt>0表示物体在向上过程中,vt<0表示物体在向下过程中;s>0表示物体在抛出点上方,s<0表示物体在抛出点下方.
电场强度:


计算场强的四种方法:
1.计算电场强度的常用方法——公式法
(1)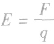 是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
是电场强度的定义式,适用于任何电场,电场中某点的场强是确定值,其大小和方向与试探电荷无关,试探电荷q充当“测量工具”的作用。
(2)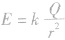 要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
要是真空中点电荷电场强度的计算式,E 由场源电荷Q和某点到场源电荷的距离r决定。
(3)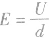 是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
是场强与电势差的关系式,只适用于匀强电场,注意式中的d为两点间的距离在场强方向的投影。
2.计算多个电荷形成的电场强度的方法——叠加法
当空间的电场由几个点电荷共同激发的时候,空间某点的电场强度等于每个点电荷单独存在时所激发的电场在该点的场强的矢量和,其合成遵循矢量合成的平行四边形定则。
3.计算特殊带电体产生的电场强度的方法
(1)补偿法对于某些物理问题,当直接去解待求的A很困难或没有条件求解时,可设法补上一个B,补偿的原则是使A+B成为一个完整的模型,从而使A+B变得易于求解,而且,补上去的B也必须容易求解。这样,待求的A便可从两者的差值中获得,问题就迎刃而解了,这就是解物理题时常用的补偿法。用这个方法可算出一些特殊的带电体所产生的电场强度。
(2)微元法在某些问题中,场源带电体的形状特殊,不能直接求解场源带电体在空间某点所产生的总电场,此时可将场源带电体分割,在高中阶段,这类问题中分割后的微元常有部分微元关于待求点对称,这就可以利用场的叠加及对称性来解题。
4.计算感应电荷产生的电场强度的常用方法—— 静电平衡法根据静电平衡时导体内部场强处处为零的特点,外部场强与感应电荷产生的场强(附加电场)的合场强为零,可知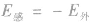 ,这样就可以把复杂问题变简单了。
,这样就可以把复杂问题变简单了。
电势能:

电势能大小的比较方法:
1.由公式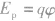 判断
判断
设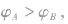 当
当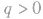 时,
时,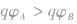 ,即
,即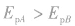 ;当
;当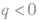 时,
时, 可总结为正电荷在电势高的地方电势能大,而负电荷在电势高的地方电势能小。
可总结为正电荷在电势高的地方电势能大,而负电荷在电势高的地方电势能小。
2.做功判断法电场力做正功,电荷(无论是正电荷还是负电荷) 从电势能较大的地方移向电势能较小的地方。反之,如果电荷克服电场力做功,那么电荷将从电势能较小的地方移向电势能较大的地方。
与“如图所示在竖直平面内建立直角坐标系XOY,OY表示竖直向上的方...”考查相似的试题有:
- 在太阳系中有一颗行星的半径为R,若在该星球表面以初速度v0竖直上抛出一物体,则该物体上升的最大高度为H。已知该物体所受的...
- 把一个q=5×10-9C的正电荷,放在电场中的A点,它受的电场力为20×10-5N,方向水平向左,则该点的场强大小为______N/C,在A点放...
- 带正电的离子M只在电场力作用下由P点运动到Q点,在此过程中克服电场力做功2.6×10-4J那么( )A.M在P点电势能一定大于Q点的电势...
- 下列描述电场的物理量中哪些与试探电荷有关?( )A.电场强度B.电势C.电势能D.电势差
- 如图所示,悬线下挂着一个带正电的小球,它的质量为m、电量为q,整个装置处于水平向右的匀强电场中,电场强度为E。则下列说法...
- 如图所示,两平行金属板P、Q相距d=1.0m,电势差为U=2v,两板间的匀强电场方向水平向右,A点与P板的距离x=0.6m.求:(1)两极...
- 如图为平行板电容器,两板间电场强度E和磁感应强度B互相垂直,某带电粒子向右恰能沿平行极板的虚线通过平行板电容器(粒子重...
- 如图所示,A、B是一条电场线上的两点,一带正电的点电荷沿电场线从A点运动到B点,在这个过程中,关于电场力做功的说法正确的...
- 带电粒子M只在电场力作用下由P点运动到Q点,在此过程中克服电场力做了2.6×10-6J的功。那么[ ]A.M在P点的电势能一定小于它在Q...
- 一对等量正点电荷电场的电场线(实线)和等势线(虚线)如图所示,图中A、B两点电场强度分别是,电势分别是,负电荷q在A、B时...