本试题 “站在升降机里的人,在升降机开始自由下落的同时,以速率vo竖直向上和沿水平方向分别抛出A、B两光滑小球.不计空气阻力.小球碰到升降机内壁后垂直内壁方向的...” 主要考查您对自由落体运动
力的合成
力的分解
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 自由落体运动
- 力的合成
- 力的分解
自由落体运动:
物体只在重力作用下从静止开始下落的运动叫做自由落体运动。
自由落体运动的公式:
v=gt;h=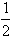 gt2;v2=2gh。
gt2;v2=2gh。
运动性质:
自由落体运动是初速度为零的匀加速直线运动。
自由落体加速度:
在同一地点,一切物体在自由落体运动中的加速度都相同,这个加速度叫自由落体加速度,也叫重力加速度。
物体做自由落体运动的条件:
①只受重力而不受其他任何力,包括空气阻力。
②从静止开始下落。
重力加速度g:
①方向:总是竖直向下的。
②大小:g=9.8m/s2,粗略计算可取g=10m/s2
③在地球上不同的地方,g的大小不同.g随纬度的增加而增大(赤道g最小,两极g最大),g随高度的增加而减小。
知识点拨:
自由落体运动的规律:
自由落体运动是初速度为零的匀加速直线运动,所以,匀变速直线运动公式也适用于自由落体运动。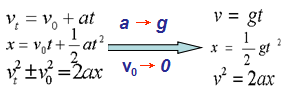
小知识--重力加速度:
①把地球当做旋转椭球,重力加速度计算公式为:g=9.7803(1+0.0052884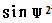 -0.0000059
-0.0000059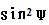 2)m/s2
2)m/s2
式中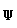 为物体所在处的地理纬度
为物体所在处的地理纬度
②重力加速度还和物体离地面的高度h有关。当h远小于地球半径R时,
小知识—空气阻力:
空气阻力是物体在空气中运动时受到的阻力。空气阻力的大小与物体相对于空气的速度、物体的形状等都有很大的关系。
当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的效果跟原来几个力的共同效果相同,这个力就叫做那几个力的合力,原来的几个力叫做这个力的分力。
①合力与分力是针对同一受力物体而言的。
②一个力之所以是其他几个力的合力,或者其他几个力之所以是这个力的分力,是冈为这一个力的作用效果与其他几个力共同作用的效果相当,合力与分力之间的关系是一种等效替代的关系。
③合力可能大于任何一个分力,也可能小于任何一个分力,也可能介于两个分力之间。
④如果两个分力的大小不变,夹角越大,合力就越小;夹角越小,合力就越大。
⑤两个大小一定的力F1、F2,其合力的大小范围
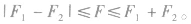

力的运算法则:
1.平行四边形定则
作用在同一点的两个互成角度的力的合力,不等于两分力的代数和,而是遵循平行四边形定则。如果以表示两个共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用这两个邻边之间的对角线表示,这叫做力的平行四边形定则,如图所示。 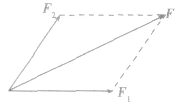
2.三角形定则和多边形定则如图(a)所示,两力F1、F2合成为F的平行四边形定则,可演变为(b)图,我们将(b)图称为三角形定则合成图,即将两分力F1、F2首尾相接,则F就是由F,的尾端指向F2的首端的有向线段所表示的力。
如果是多个力合成,则由三角形定则合成推广可得到多边形定则,如图为三个力F1,F2、F3的合成图,F 为其合力。
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
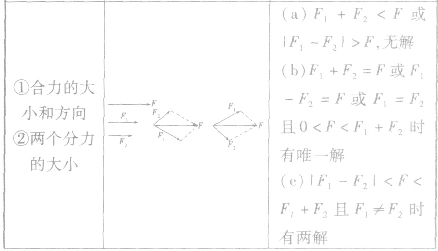
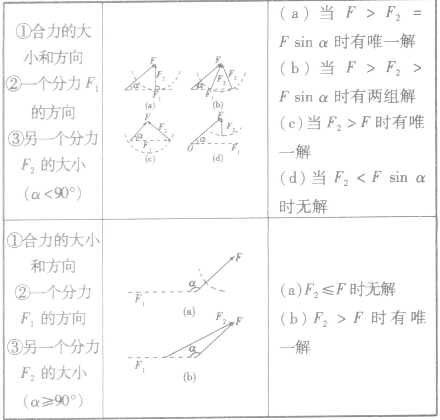
力的分解的几种情况:
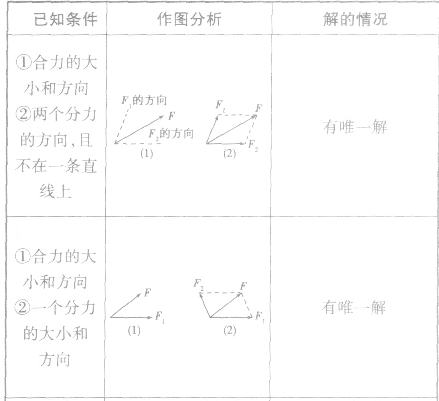
分解方法:
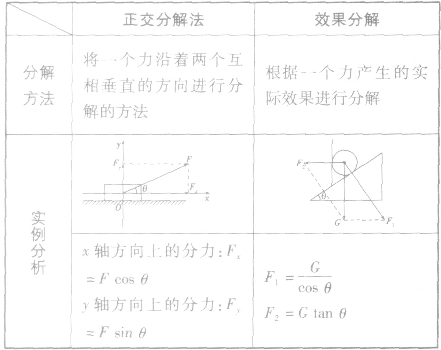
几种按效果分解的实例:


由力的三角形定则求力的最小值:
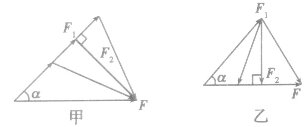
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值
 。
。 (2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值
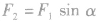 。
。
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值
 。
。由圆的切线求力方向的极值:
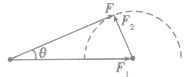
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足
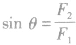 。
。 
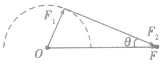
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足
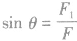 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足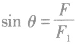 。
。
与“站在升降机里的人,在升降机开始自由下落的同时,以速率vo竖...”考查相似的试题有:
- 离地高h=500m的空中自由落下一个小球,不计空气阻力,取g=10m/s2.求:(1)小球落到地面经过的时间t1;(2)小球落地前最后1...
- 一物体从H高处自由下落,经t时间落地,则当下落t3时,离地高度为( )A.H3B.H9C.3H4D.8H9
- 关于自由落体运动,以下说法正确的是( )A.自由落体运动是匀加速直线运动,初速度为零,加速度大小恒等于g,加速度的方向竖...
- 竖直竹杆长9m,它的下端离1m高的窗口上沿1.25m,放手让竹杆自由下落,它通过窗口所需的时间为:(g取10m/s2)( )A.1 sB.1.25...
- 自由下落的物体,忽略空气阻力,其动能与位移的关系如图所示,则图中直线的斜率表示( )A.质量B.势能C.重力大小D.重力加...
- 固定在地面上、绝缘材料制成的半球形碗,内壁光滑,球心为O点,碗底固定一个带正电的点电荷A,另一个也带正电的点电荷B,质量...
- 如图所示,两平行光滑导轨相距0.2m,与水平面夹角为300,金属棒MN的质量为0.2kg,金属棒的电阻R=1Ω,其处在与轨道平面垂直且...
- 如图所示,OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的O点,另一端与静止在动摩擦因数恒定的水平地面上的滑块A相连...
- 甲、乙两人用绳子拉船,使船沿OO′方向航行,甲用1000N的力拉绳子,方向如图所示,要使船沿OO′方向行驶,乙的拉力至少应多大?...
- 世界上第一枚原子弹爆炸时,恩里克•费米把事先准备好的碎纸片从头顶上撒下,碎纸片落到他身后约 2m 处,由此,他根据估算出的...