本试题 “两条彼此平行、间距为l=0.5m的光滑金属导轨水平固定放置,导轨左端接一电阻,其阻值R=2Ω,右端接阻值RL=4Ω的小灯泡,如下面左图所示.在导轨的MNQP矩形区域内...” 主要考查您对闭合电路欧姆定律
法拉第电磁感应定律
导体切割磁感线时的感应电动势
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 闭合电路欧姆定律
- 法拉第电磁感应定律
- 导体切割磁感线时的感应电动势
闭合电路欧姆定律:
1、内容:闭合电路的电流强度跟电源的电动势成正比,跟闭合电路总电阻成反比。
2、表达式:I=E/(R+r)。
3、适用范围:纯电阻电路。
4、电路的动态分析:
①分析的顺序:外电路部分电路变化→R总变化→由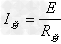 判断I总的变化→由U=E-I总r判断U的变化→由部分电路欧姆定律分析固定电阻的电流、电压的变化欧→用串、并联规律分析变化电阻的电流、电压电功。
判断I总的变化→由U=E-I总r判断U的变化→由部分电路欧姆定律分析固定电阻的电流、电压的变化欧→用串、并联规律分析变化电阻的电流、电压电功。
②几个有用的结论
Ⅰ、外电路中任何一个电阻增大(或减少)时外电路的总电阻一定增大(或减少)。
Ⅱ、若开关的通断使串联的用电器增多时,总电阻增大;若开关的通断使并联的支路增多时,总电阻减少。
Ⅲ、动态电路的变化一般遵循“串反并同”的规律;当某一电阻阻值增大时,与该电阻串联的用电器的电压(或电流)减小,与该电阻并联的用电器的电压(或电流)增大。
电源的 关系:
关系:



电阻的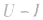 图像与闭合电路的
图像与闭合电路的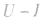 图像:
图像: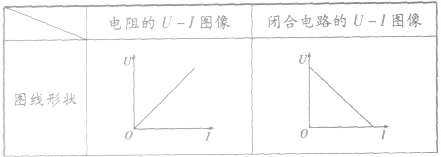

法拉第电磁感应定律:
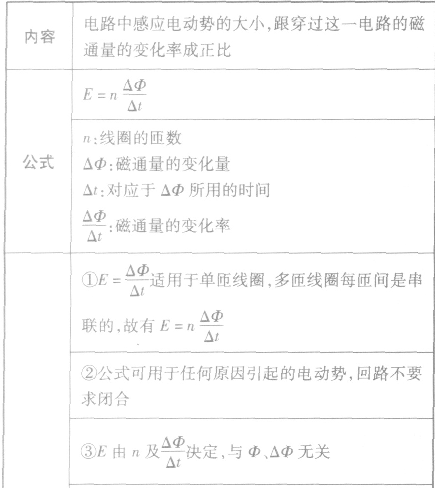

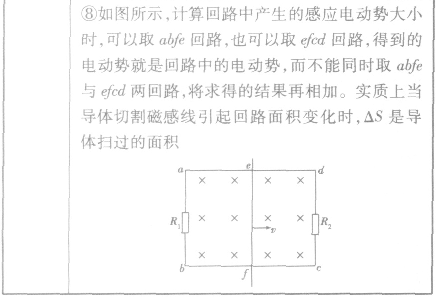
导体切割磁感线的两个特例:

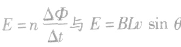 的区别与联系及选用原则:
的区别与联系及选用原则: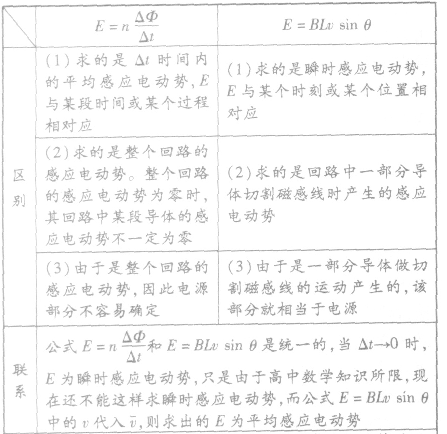

电磁感应中动力学问题的解法:
电磁感应和力学问题的综合,其联系的桥梁是磁场对感应电流的安培力,因为感应电流与导体运动的加速度有相互制约的关系。
1.分析思路
(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向。
(2)求回路中的电流。
(3)分析研究导体受力情况(包含安培力,用左手定则确定其方向)。
(4)列动力学方程或平衡方程求解。
2.常见的动态分析这类问题中的导体一般不是做匀变速运动,而是经历一个动态变化过程再趋于一个稳定状态,故解这类问题时正确进行动态分析确定最终状态是解题的关键。同时也要抓好受力情况和运动情况的动态分析,研究顺序为:导体受力运动产生感应电动势一感应电流一通电导体受安培力一合外力变化一加速度变化一速度变化一周而复始地循环,循环结束时,加速度等于零.导体达到稳定运动状态。
电磁感应中的动力学临界问题:
(1)解决这类问题的关键是通过运动状态的分析,寻找过程中的临界状态,如速度、加速度求最大值或最小值的条件。
(2)基本思路: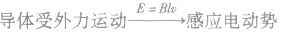
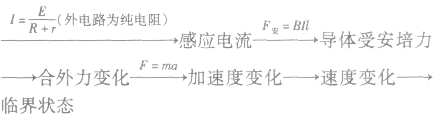
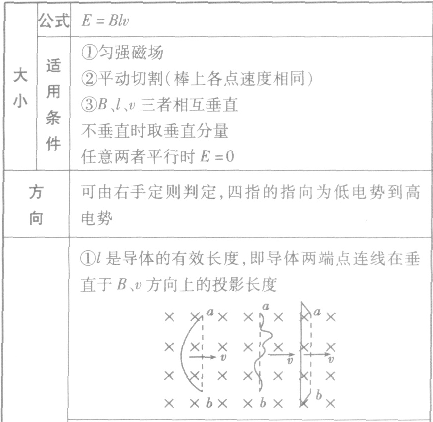
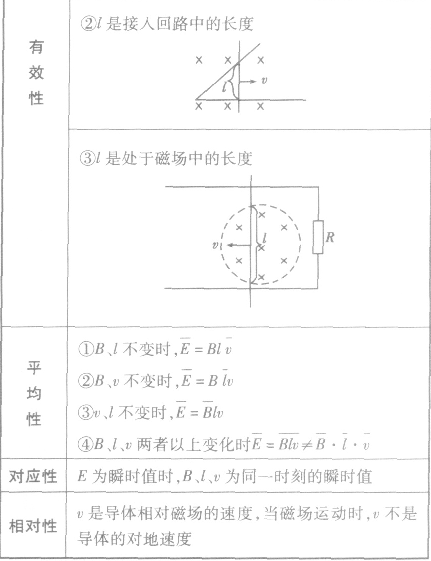
导体切割磁感线产生的电动势:
电磁感应中电路问题的解法:
电磁感应规律与闭合电路欧姆定律相结合的问题,主要涉及电路的分析与计算。解此类问题的基本思路是:
(1)找电源:哪部分电路产生了电磁感应现象,则这部分电路就是电源。
(2)由法拉第电磁感应定律求出感应电动势的大小,根据楞次定律或右手定则确定出电源的正负极。
①在外电路,电流从正极流向负极;在内电路,电流从负极流向正极。
②存在双感应电动势的问题中,要求出总的电动势。
(3)正确分析电路的结构,画出等效电路图。
①内电路:“切割”磁感线的导体和磁通量发生变化的线圈都相当于“电源”,该部分导体的电阻相当于内电阻。
②外电路:除“电源”以外的电路即外电路。
(4)运用闭合电路欧姆定律、串并联电路特点、电功率等列方程求解。
与“两条彼此平行、间距为l=0.5m的光滑金属导轨水平固定放置,导...”考查相似的试题有:
- 在如图所示的电路中,当变阻器R3的滑动头P由a端向b端移动时[ ]A、电压表示数变大,电流表示数变小B、电压表示数变小,电流表...
- 如图6所示电路,闭合开关S,灯泡不亮,电流表无示数,而电压表指针有明显偏转,该电路的故障可能是( )A.电流表坏了或是与...
- 如图所示电路中,电源电动势为E、内阻为r,电阻R3为定值电阻,R1,R2为滑动变阻器,A,B为电容器两个水平放置的极板,当滑动...
- 在图所示的电路中,合上电键S后,( )A.电流表读数变大,电压表读数变大B.电流表读数变小,电压表读数变小C.电流表读数变...
- 图示是测磁感应强度的一种装置.把一个很小的测量线圈放在待测处,将线圈跟冲击电流计G串联(冲击电流计是一种测量电量的仪器...
- 有一个100匝的线圈,总电阻为10Ω,在0.2s内垂直穿过线圈平面的磁通量从0.02Wb均匀增加到0.1Wb.问:(1)这段时间内线圈中产...
- 如图所示,U形导线框MNQP水平放置在磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距...
- (20分)其同学设计一个发电测速装置,工作原理如图所示。一个半径为R=0.1m的圆形金属导轨固定在竖直平面上,一根长为R的金属...
- 如图所示,矩形线框abcd可以在两根平行的金属导轨MN.PQ上滑动,把它们放在磁场中,当线框向右滑动时,下列说法哪个正确?( ...
- 试根据法拉第电磁感应定律E=n△Φ△t,推导出导线切割磁感线产生的感应电动势大小的表达式E=BLv.(即在B⊥L,v⊥L,v⊥B的条件下,...