本试题 “不定项选择在电磁学发展过程中,许多科学家做出了贡献,下列说法正确的是( )A.奥斯特发现了电流磁效应,法拉第发现了电磁感应定律B.洛伦兹发现了磁场对电流...” 主要考查您对电荷、元电荷
电流的磁效应
磁场对通电导线的作用:安培力、左手定则
磁场对运动电荷的作用:洛伦兹力、左手定则
法拉第电磁感应定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 电荷、元电荷
- 电流的磁效应
- 磁场对通电导线的作用:安培力、左手定则
- 磁场对运动电荷的作用:洛伦兹力、左手定则
- 法拉第电磁感应定律
电荷、电荷守恒定律:
1.涉及电荷的基本概念
(1)电荷自然界中存在着两种电荷,它们分别为正电荷和负电荷。用毛皮摩擦过的橡胶棒上带的电荷叫负电荷,用丝绸摩擦过的玻璃棒上带的电荷叫正电荷。同种电荷互相排斥,异种电荷互相吸引。
(2)电荷量电荷量是指物体带电的多少。电荷量是电荷的定量量度。正电荷的电荷量为正值,负电荷的电荷量为负值。尽管电荷量有正、负值(正号一般省略),但要知道这里的“+”、“-”号代表电荷的性质(种类),与数学中的正、负号的含义不同。在国际单位制中,电荷量的单位是库仑,简称库,符号c。
(3)元电荷电子和质子带有等量的异种电荷,其电荷量e: 1.60×10-19C,称为元电荷,用e表示。所有带电体的电荷量都是元电荷e的整数倍,这就是说电荷量是不能连续变化的物理量。无电荷不是电荷,它是指电荷的电荷量,电荷量1.60×10-19C称为元电荷。元电荷的数值最早是由美国科学家密立根用实验测得的。所有带电体的电荷量等于元电荷或者等于元电荷的整数倍。质子、电子都不叫元电荷,它们电荷量的绝对值才叫元电荷。
(4)点电荷形状和大小对研究问题的影响可以忽略的带电体称为点电荷。
①点电荷是无大小、无形状、只有电荷量的一个理想化模型。在实际问题中,只有当带电体间的距离比它们自身的大小大得多,以至于带电体的形状和大小对相互作用力的影响可以忽略不计时,带电体才可以被视为点电荷。
②一个带电体能否被视为点电荷完全取决于自身的几何形状、大小与其他带电体之间的距离的比较。即带电体很小,不一定可被视为点电荷,带电体很大,也不一定不能被视为点电荷。
(5)感应电荷当一个带电体靠近导体时,南于电荷间相互吸引或排斥,导体中的自由电荷便会趋向或远离带电体,使导体靠近带电体的一端带异号电荷,远离带电体的一端带同号电荷。这种现象叫做静电感应。由于静电感应而使导体两端出现的等量异号电荷通常叫做感应电荷。其特点是:不带电导体靠近带电体时,靠近带电体的一端出现与带电体电性相反的电荷,远离带电体的一端出现与带电体电性相同的电荷。
(6)场源电荷电场是由电荷产生的,我们把产生电场的电荷叫做场源电荷。
(7)试探电荷研究电场的基本方法之一是在电场中放入一带电荷量很小的点电荷,分析其受力和能量情况,借以研究电场的性质,这样的电荷称为试探电荷。作为试探电荷的带电体,基本要求是体积要小,能研究电场中每一点的性质,还要求带电体所带电荷量要少.以放入试探电荷后试探电荷对原电场的影响可忽略为原则。
(8)净电荷物体带电实质是得到或失去了电子,讨论物体带何种电荷,所带电荷量是多少,是指物体的净电荷是正还是负,物体所具有的总电荷中正、负电荷的差值是多少,电荷量是物体中净电荷的多少。
(9)比荷带电体所带电荷量与其质量之比叫做该带电体的比荷。比荷是一个重要的物理量,常用来描述微观粒子的性质,在国际单位制中其单位为库仑每千克,符号 C/kg。
1、概念:电流能产生磁场,这个现象称为电流的磁效应
2、奥斯特实验:奥斯特通过实验发现,水平电流在小磁针的正上方或正下方,且电流方向沿南北方向时小磁针发生明显偏转,如图所示
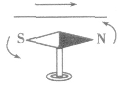
首次揭示了电与磁的联系
安培力与洛伦兹力:
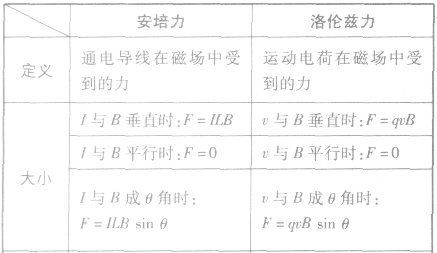

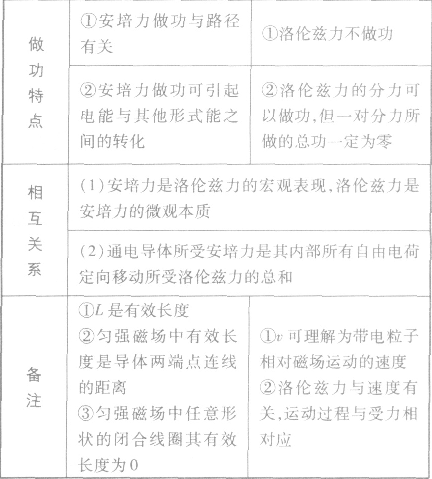
通电导线在安培力作用下运动方向的判定方法:
要判定通电导线在安培力作用下的运动,首先必须清楚导线所在位置磁场的分布情况,然后才能结合左手定则准确判定导线的受力情况,进而确定导线的运动方向。常用的方法如下: 1.电流元法
(1)同一磁场中的弯曲导线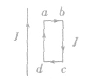
把整段弯曲导线分为多段直线电流元,先用左手定则判定每段电流元受力的方向,然后判定整段导线所受合力的方向,从而确定导线的运动方向,如在图中,要判定导线框abcd的受力可将其分为四段来判定,若将导线框换作导线环时,可将其分为多段直线电流元。
(2)不同磁场区域中的直线电流当直导线处于不同的磁场区域中时,可根据导线本身所处的物理情景,将导线适当分段处理,如图甲中,要判定可自由运动的通电直导线AB在蹄形磁铁作用下的运动情况时,以蹄形磁铁的中轴线OO’为界,直导线在OO’两侧所处的磁场截然不同,则可将AB以OO’为分界点分为左右两段来判定。 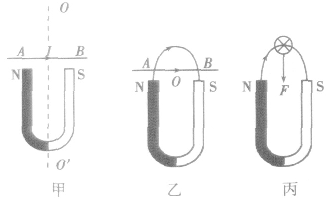
2.特殊位置法因电流所受安培力的方向是垂直于电流和磁场所决定的平面的,虽然电流与磁场之间夹角不同时电流所受安培力大小不同,但所受安培力的方向是不变的 (要求电流从平行于磁场的位置转过的角度不超过 180。)。故可通过转动通电导线到某个便于分析的特殊位置,然后判定其所受安培力的方向,从而确定其运动方向。如在上图甲中,初始位置磁场在平行于电流方向上的分量对电流无作用力,但一旦离开初始位置,此磁场分量就会对电流产生作用力,如上图乙所示。但此分量对电流在转动过程中作用力的方向不方便判定.可将此导线转过90。,此时电流方向与该磁场分量方向垂直,用左手定则很容易判定出受力方向,如上图丙所示,
3.等效法
(1)从磁体或电流角度等效
环形电流可以等效成小磁针,通电螺线管可以等效成条形磁铁或多个环形电流,反过来等效也成立。将环形电流与小磁针相互等效时,它们的位置关系可以认为是小磁针位于环形电流的中心处,N、S极连线与环面垂直,且N、S极与电流方向遵从安培定则。如在图中,两通电圆环同心,所在平面垂直,要判定可自南转动的圆环,I2的运动情况,可将其等效为一小磁针。 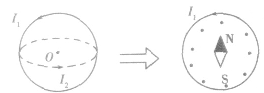
(2)从磁感线分布情况的角度等效
根据要判定的电流或磁体所在处的磁感线分布,将其所在处的磁场等效为某一能够在该处产生类似磁场的场源电流或磁体,然后再用电流之间或磁体之间相互作用的规律来判定。如在图中,导线AB所在处的磁感线分布与位于其下方与纸面垂直的通电直导线在该处产生的磁感线类似(注意是类似而不是相同),所以可以将蹄形磁铁等效为一通电直导线进而进行判定。 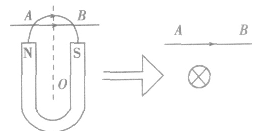
4.结论法
当两电流之间或两等效电流之间发生相互作用时,可利用电流之间相互作用的规律直接判定,只是同前所述,此法应慎用。
(1)两平行直线电流在相互作用过程中,无转动趋势,同向电流互相吸引,反向电流互相排斥;
(2)两不平行的直线电流互相作用时,有转到平行且电流方向相同的趋势。
5.转换研究对象法
定性分析磁体在电流磁场作用下如何运动的问题,可先分析电流在磁体磁场中所受的安培力,然后由牛顿第三定律,确定磁体所受电流磁场的作用力,从而确定磁体所受的合力及运动方向。如在图中要判定磁铁所受电流的作用力,可以分析磁铁对电流的作用力。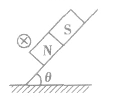
安培力作用下力学问题的解决方法:
由于安培力的方向总是垂直于电流方向与磁场方向决定的平面,即F一定垂直于B和I,但B和I不一定垂直。因此涉及安培力的问题常呈现于三维空间中,要解决这类问题,需从合适的方位将立体图改画为二维平面图,再通过受力分析及运动情况分析,结合平衡条件或牛顿运动定律解题。
安培力与洛伦兹力:
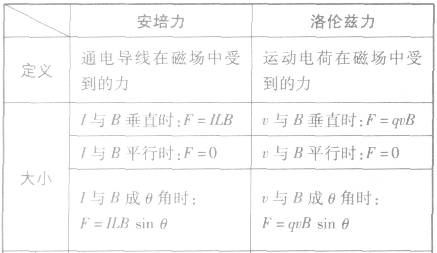

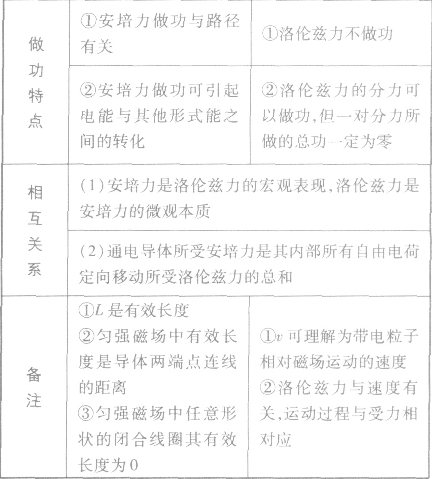
洛伦兹力作用下力学问题的解决方法:
(1)涉及洛伦兹力的动力学问题中,因洛伦兹力的大小和方向与物体的运动状态有关,在分析物体的运动过程时,需将运动对受力的影响、受力对运动的影响综合考虑来确定物体的运动性质及运动过程,此类问题中往往还会出现临界状态,需分析临界状态下满足的条件。
(2)在涉及洛伦兹力的能量问题中,因洛伦兹力不做功,系统能量的转化取决于其他力做功的情况,但需考虑洛伦兹力对最终运动状态的影响。
(3)在定性判定涉及洛伦兹力的非匀变速运动过程中,可利用运动的合成与分解来定性地判定通过的位移、运动的时间等问题。
法拉第电磁感应定律:
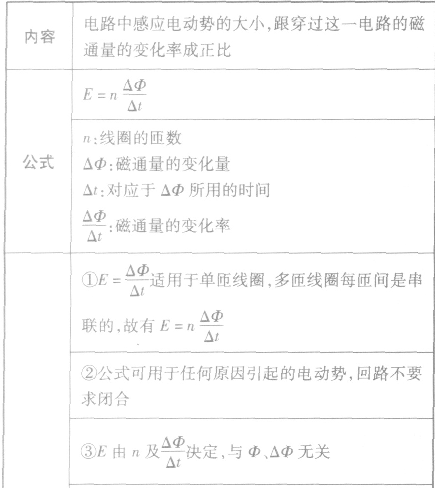

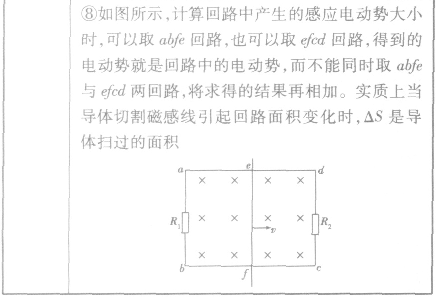
导体切割磁感线的两个特例:

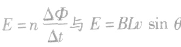 的区别与联系及选用原则:
的区别与联系及选用原则: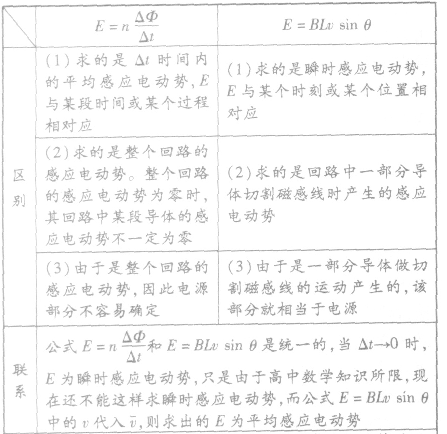

电磁感应中动力学问题的解法:
电磁感应和力学问题的综合,其联系的桥梁是磁场对感应电流的安培力,因为感应电流与导体运动的加速度有相互制约的关系。
1.分析思路
(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向。
(2)求回路中的电流。
(3)分析研究导体受力情况(包含安培力,用左手定则确定其方向)。
(4)列动力学方程或平衡方程求解。
2.常见的动态分析这类问题中的导体一般不是做匀变速运动,而是经历一个动态变化过程再趋于一个稳定状态,故解这类问题时正确进行动态分析确定最终状态是解题的关键。同时也要抓好受力情况和运动情况的动态分析,研究顺序为:导体受力运动产生感应电动势一感应电流一通电导体受安培力一合外力变化一加速度变化一速度变化一周而复始地循环,循环结束时,加速度等于零.导体达到稳定运动状态。
电磁感应中的动力学临界问题:
(1)解决这类问题的关键是通过运动状态的分析,寻找过程中的临界状态,如速度、加速度求最大值或最小值的条件。
(2)基本思路: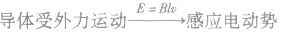
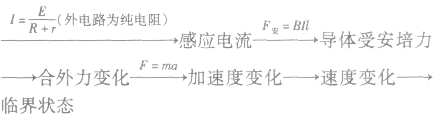
与“不定项选择在电磁学发展过程中,许多科学家做出了贡献,下列...”考查相似的试题有:
- 如图所示,PQ和MN为水平、平行放置的金属导轨,相距1m,导体棒ab跨放在导轨上,棒的质量m=0.2kg,棒的中点用细绳经滑轮与物体...
- 在磁感应强度是4.0×10-2T的匀强磁场中,有一条与磁场方向垂直的导线ab,导线长为8 cm,通有2.5 A的电流,方向由a到b,如图所...
- 在图中,单摆的摆线是绝缘的,长为l,摆球带正电,单摆悬挂于O点,当它摆过竖直线OC时,便进入或离开一个匀强磁场,磁场的方...
- 下列说法中正确的是( )A.带电粒子在磁场中运动时,一定受到洛伦兹力作用B.磁感应强度、洛伦兹力、粒子的速度三者之间一定...
- 如图所示,一根光滑的绝缘斜槽连接一个竖放置的半径为R=0.50m的圆形绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应...
- (本题供使用选修3-1教材的考生作答.)在匀强磁场中,一带电粒子沿着垂直磁感应强度的方向运动.现将该磁场的磁感应强度增大...
- 如图,MN是匀强磁场中的一块薄金属板,带电粒子(不计重力)在匀强磁场中运动并穿过金属板,运动轨迹如图中曲线,则可判定( )...
- 如图15-5-14所示,在第Ⅰ象限内有垂直纸面向里的匀强磁场.一对正、负电子分别以相同速率,沿与x轴成30°的方向从原点射入磁场,...
- 关于物理学研究方法,下列叙述中正确的是( )A.伽利略在研究自由落体运动时采用了微量放大的方法B.用点电荷来代替实际带电...
- 如图所示电路中,自感系数较大的线圈L的直流电阻不计,下列操作中能使电容器C的A板带正电的是A.S闭合的瞬间;B.S断开的瞬间...