本试题 “图示为一列简谐横波在介质中同一区域传播的情况,实线为t1时刻波形图;虚线为t2时刻波形图,已知。(1)如果这列波向右传播,波速多大?(2)如果这列波向左...” 主要考查您对波的图像
波长、频率和波速
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 波的图像
- 波长、频率和波速
波动图像:
1.概念:表示波的传播方向上,介质中的各个质点在同一时刻相对平衡位置的位移。
2.意义:波在传播过程中各质点在某时刻的位移情况
3.特点:
①波形图线是正弦或余弦曲线的波称为简谐波。简谐波是最简单的波。对于简谐波而言,各个质点振动的最大位移都相同
②波的图像的重复性:相隔时间为周期整数倍的两个时刻的波形相同
③波的传播方向的双向性:不指定波的传播方向时,图像中波可能向x轴正向或x轴负向传播
4.应用特点:
(1)从图像上直接读出波长和振幅。
(2)可确定任一质点在该时刻的位移。
(3)可确定任一质点在该时刻的加速度方向。
(4)若知道波速v的方向,可知各质点的运动方向。
(5)若知道该时刻某质点的运动方向,可判断波的传播方向。
(6)若已知波速v的大小,可求频率f或周期T:
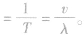
(7)若已知f或T,可求v的大小: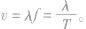
(8)若已知波速v的大小和方向,可画出在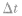 前后的波形图,即波沿着(或逆着)传播方向平移
前后的波形图,即波沿着(或逆着)传播方向平移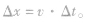
(9)结合波的图像,可确定任一质点的振动图像
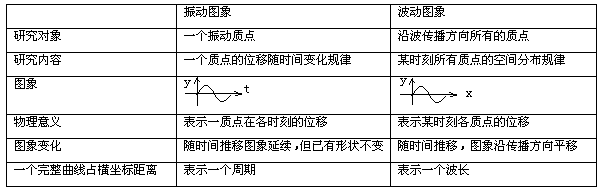
波动图像与振动图像的比较:
已知波速v和波形,画出再经△t时间波形图的方法:
1.特殊点法
在波形图上找两特殊点,如过平衡位置的点和与它相邻的峰(符)点,先确定这两点的振动方向,再看 。由于经nT时间波形不变,所以采取去整nT留零t的方法,分别作出两特殊点经t时间后的位置,然后按正弦规律画出新波形图。
。由于经nT时间波形不变,所以采取去整nT留零t的方法,分别作出两特殊点经t时间后的位置,然后按正弦规律画出新波形图。
2.平移法一——移波形
先算出经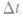 时间波传播的距离
时间波传播的距离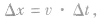 ,再把波形沿波的传播方向平移
,再把波形沿波的传播方向平移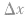 即可。因为波动图像的重复性,若已知波长λ,则波形平移n个λ时波形不变。当
即可。因为波动图像的重复性,若已知波长λ,则波形平移n个λ时波形不变。当 时,可采取去整
时,可采取去整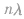 留零x的方法,只需平移x即可。
留零x的方法,只需平移x即可。
3.平移法二——移坐标轴
计算方法同上,将坐标轴y逆着波的传播方向平移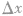 即可.
即可.
已知两不同时刻波动图像类问题的解法:
如图所示,已知某简谐波在t与t+△t时刻的波形图,从图上可以确定该波的波长λ、振幅A。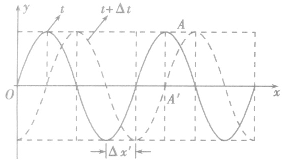
在求解波的周期、波速时有两种方法:
(1)传播的观点
由波形图可知,波在△t时间内传播的距离为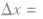
 (波沿x轴正向传}
(波沿x轴正向传}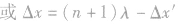 (波沿x轴负向传播)时,则波速
(波沿x轴负向传播)时,则波速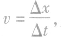 周期
周期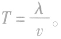
(2)振动观点
在波形图中取某一质点,比较该质点(如图中A) 在两时刻的位置和状态,确定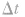 与周期的关系,如在图中,波向右传播时
与周期的关系,如在图中,波向右传播时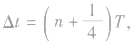 波向左传播时,
波向左传播时,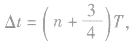 ,可求得周期的表达式,再由
,可求得周期的表达式,再由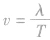 可求得波速。在这类题目中,同时应注意对时间的限制,当
可求得波速。在这类题目中,同时应注意对时间的限制,当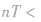
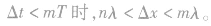
振动图像与波动图像相结合问题的解法:
解决两种图像相结合问题的基本思路
(1)首先识别哪一个是波动图像,哪一个是振动图像,两者间的联系纽带是周期与振幅。
(2)然后确定振动图像对应于波动图像中的哪一个质点,波动图像对应于振动图像中的哪一个时刻。
(3)再从振动图像中找出该质点在波动图像中的那一时刻的振动方向,然后再确定波的传播方向及其他问题。
波动图像中多解性问题的解法:
波动图像问题中的多解性涉及:
(1)波的空间周期性;
(2)波的时间周期性;
(3)波的双向性;
(4)波的对称性;
(5)介质中两质点间的距离与波长关系未定;
(6)介质中质点的振动方向未定。具体讨论如下:
①波的空间周期性
沿波的传播方向,在x轴上任取一点P(x),如图所示。P点的振动完全重复波源O点的振动,只是时间上比O点要落后出时间,且 在同一列波上,凡坐标与P点坐标x之差为波长整数倍的质点,在同一时刻t的振动位移都与坐标为x的质点的振动位移相同,其振动速度、加速度也都与坐标为x的质点相同,或者说它们的振动“相貌”完全相同。因此在同一列波上,某一振动“相貌”势必会不断地重复出现,这就是机械波的空间周期性。波的空间周期性说明,在同一列波上,相距为波长整数倍的多个质点的振动情况完全相同。
在同一列波上,凡坐标与P点坐标x之差为波长整数倍的质点,在同一时刻t的振动位移都与坐标为x的质点的振动位移相同,其振动速度、加速度也都与坐标为x的质点相同,或者说它们的振动“相貌”完全相同。因此在同一列波上,某一振动“相貌”势必会不断地重复出现,这就是机械波的空间周期性。波的空间周期性说明,在同一列波上,相距为波长整数倍的多个质点的振动情况完全相同。 
②波的时间周期性
在x轴上取一给定质点,在t+kT时刻的振动情况与它在t时刻的振动情况(位移、速度、加速度等)相同。因此在t时刻的波形,在t+kT时刻必然多次重复出现,这就是机械波的时间周期性。
波的时间周期性表明,波在传播过程中,经过整数倍周期时,其波形图线相同。
③波的双向性
双向性是指波沿正、负两方向传播时,若沿正、负两方向传播的时间之和等于周期的整数倍,则沿正、负两方向传播到那一时刻的波形图相同。
④波的对称性
波源的振动,要带动它左、右相邻质点的振动,波要向左、右两方向传播。对称性是指波在向左、右同时传播时,关于波源对称的左、右两质点的振动情况完全相同。
⑤介质中两质点间的距离与波长关系未定
在波的传播方向上,如果两个质点间的距离不确定,就会形成多解,学生若不能联想到所有可能的情况,则易出现漏解。
⑥介质中质点的振动方向未定
在波的传播过程中,质点振动方向与传播方向相联系,若某一质点振动方向未确定,则波的传播方向有两种,这样会形成多解。
波长:
1.定义:在波动中,振动相位总是相同的两个相邻质点间的距离,叫做波长,通常用λ表示
另一种定义方式:两个相邻的、在振动过程中对平衡位置的位移总是相等的质点间的距离叫波长
2.意义:波长反映了波在空间的周期性
平衡位置相距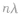 的质点振动相同,平衡位置相距
的质点振动相同,平衡位置相距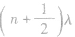 的质点振动相反(其中n=0,l,2…)
的质点振动相反(其中n=0,l,2…)
3.备注:①注意定义中两个要素:“总是”,“相邻”
②在横波中两个相邻的波峰(或波谷)间的距离等于波长。在纵波中两个相邻的密部(或疏部)间的距离等于波长。
③在一个周期内机械波传播的距离等于一个波长
周期与频率:
1.概念:在波动中,各个质点的振动周期或频率是相同的,它们都等于波源的振动周期或频率,这个周期或频率也叫做波的周期或频率
2.关系:频率与周期的关系:
3.备注:①波源振动一个周期,被波源带动的质点刚好完成一个全振动,波在介质中传播一个波长
②波的频率等于单位时间内波形成完整波的个数;等于单位时间内通过介质中某点完整波形的个数;等于介质内已开始振动的任一质点在单位时间内完成全振动的次数;等于单位时间内沿波传播方向上传播距离与波长的比值,即传播距离内包含完整波形的个数
③每经历一个周期,波形图重复一次
波速:
1.定义:单位时间内振动向外传播的距离
2.定义式:
3.意义:波速是指振动在介质中传播的快慢程度
4.备注:波速与质点振动速度不同,且与其无关
三者关系:
1.定量关系:经过一个周期T,振动在介质中传播的距离等于一个波长λ,所以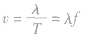
2.决定因素:(1)周期T和频率f取决于波源,与v、λ无关,与介质无关。波从一种介质进人另一种介质时,周期和频率是不变的。
(2)波速v由介质本身性质决定,与f,λ无关。
(3)波长λ决定于v和f(或T),只要v和f其中一个改变,λ就改变
质点振动方向与波的传播方向的互判方法:
已知质点的振动方向可判断波的传播方向;相反,已知波的传播方向可判断质点的振动方向。
1.上下坡法
沿波的传播方向看,“上坡”的点向下振动,“下坡”的点向上振动,简称“上坡下,下坡上”。如图所示。
逆着波的传播方向看,“上坡”的点向上振动,“下坡’’的点向下振动。 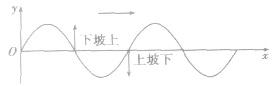
2.同侧法
在波的图像上的某一点,沿纵轴方向画出一个箭头表示质点振动方向,并设想在同一点沿x轴方向画一个箭头表示波的传播方向,那么这两个箭头总是在曲线的同侧。如图所示。 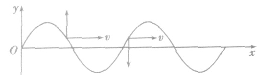
3.带动法(特殊点法)
如图所示为一沿x轴正方向传播的横波,根据波的形成,靠近波源的点能带动它邻近的离波源稍远的点,可判断质点的振动方向。在质点P附近靠近波源一方的图线上另找一点P',若P’在P上方,P '带动P向上运动,则P向上运动;若P’在P下方,P带动 P’向下运动,则P’向下运动。 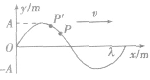
4.微平移法
将波形沿波的传播方向做微小移动,如图中虚线所示,由于质点仅在y轴方向上振动,所以,
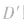 即质点运动后的位置,故该时刻A、B沿y轴正方向运动,C、D沿y轴负方向运动。
即质点运动后的位置,故该时刻A、B沿y轴正方向运动,C、D沿y轴负方向运动。
与“图示为一列简谐横波在介质中同一区域传播的情况,实线为t1时...”考查相似的试题有:
- 一简谐横波在x轴上传播,波源振动周期T="0.1" s,在某一时刻的波形如图11-1所示,且此时a点向下运动,则( )图11-1A.波速为2...
- (4分)如图所示为一列简谐波在时刻的图象,已知质点M的振动方程为(cm),此波中质点M在 s时恰好第3次到达y轴正方向最大位移...
- 图中实线和虚线分别是x轴上传播的一列简谐横波在t=0和t=0.03s时刻的波形图,已知x=1.2m处的质点在t=0.03s时刻向y轴正方向运动...
- 如图所示,沿波的传播方向上有间距为1m的13个质点a,b,c,d,e,g,h,i,j,k,l,m,它们均静止在各自的平衡位置,一列横...
- 【选修3-4选做题】一列沿x轴正向传播的横波在某时刻的波形图如图甲所示。a、b、c、d为介质中沿波的传播方向上四个质点的平衡...
- 一列简谐横波沿x轴传播,t=0时刻的波形如图所示,则从图中可以看出这列波的波长为5m波中的每个质点的振动周期为4s若已知波沿x轴...
- (1)下列说法正确的是______________;A.光的偏振现象说明光是纵波B.全息照相利用了激光相干性好的特性C.光导纤维传播光...
- 一列沿x轴正方向传播的横波,某时刻的波形图象如图中的Ⅰ所示,经t=0.2 s后,波形图象如图中Ⅱ所示.求这列波的波速.
- 如图所示,沿波的传播方向上有间距为1m的13个质点a.b.c.d.e.f.g.h.I.j.k.l.m,它们均静止在各自的平衡位置.一列...
- 关于机械波下列说法错误的是;( )A.任一质点振动每经过一个周期,波沿传播方向移动一个波长B.波的产生需要两个条件,即波...