本试题 “为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不等的小球,按下述步骤进行实...” 主要考查您对碰撞
实验:验证动量守恒定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 碰撞
- 实验:验证动量守恒定律
1、特点:
①时间:过程持续时间即相互作用时间极短
②作用力:在相互作用的过程中,相互作用力先是急剧增大,然后再急剧减小,平均作用力很大
③动量守恒条件:系统的内力远远大于外力,所以,系统即使所受外力之和不为零,外力也可以忽略,系统的总动量守恒
④位移:碰撞过程是在一瞬间发生的,时间极短,所以,在物体发生碰撞的瞬间,可忽略物体的位移,可以认为物体在碰撞前后仍在同一位置
⑤能量:在碰撞过程中,一般伴随着机械能的损失,碰撞后系统的总动能要小于或等于碰撞前系统的总动能,
2、两物体相碰通常有以下三种情况
①两物体碰撞后,动能无损失,称为弹性碰撞。当两相等质量的物体发生弹性碰撞时,则发生速度交换,这是一个很有用的结论。
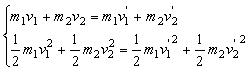
②两物体碰撞后虽分开,但动能有损失,称为非弹性碰撞。
③两物体碰撞后合为一个整体,以某一共同速度运动,称为完全非弹性碰撞。此类碰撞中动能损失最多,即动能转化为其他形式能的值最多。
弹性碰撞及讨论:
质量为m1与质量为m2的物体分别以速度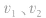 运动并发生对心碰撞,碰撞过程中无机械能损失(如图所示)。
运动并发生对心碰撞,碰撞过程中无机械能损失(如图所示)。
设碰后两物体的速度分别为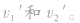
据动量守恒得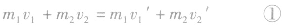
据机械能守恒得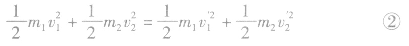
由①②两式得
由上述表达式可以看出:
(1)若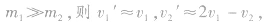
(2)若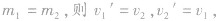 即速度交换。
即速度交换。
(3)若 ,即m2的速度几乎不变。
,即m2的速度几乎不变。
“一动一静”模型:
(1)弹性正碰,如图所示,在光滑水平面上质量为 m1的小球以速度v1与质量为m2的静止小球发生弹性正碰.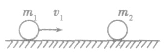
讨论碰后两球的速度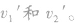 根据动量守恒和机械能守恒有:
根据动量守恒和机械能守恒有: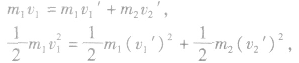
解上面两式可得:
碰后m1的速度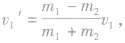
碰后m2的速度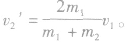
讨论:
①若表示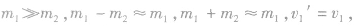
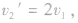 表示m1的速度不变,m2以2v1速度被撞出去。
表示m1的速度不变,m2以2v1速度被撞出去。
②若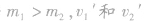 都是正值,表示
都是正值,表示 都与v1方向相同。
都与v1方向相同。
③若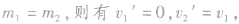 ,则有即碰后两球速度互换。
,则有即碰后两球速度互换。
④若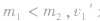 为负值,表示
为负值,表示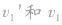 方向相反, m1被弹回。
方向相反, m1被弹回。
⑤若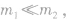 这时
这时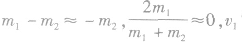
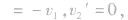 表示m1被反向以原速率弹回,而m2仍静止。
表示m1被反向以原速率弹回,而m2仍静止。
⑥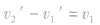
两物体碰后的速度随两物体的质量比变化情况如图所示。 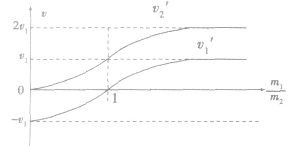
⑦能量传递:在弹性碰撞中,传递的能量跟两者质量比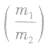 有关,即
有关,即
 两球质量越接近,碰撞中传递的动能越大;在
两球质量越接近,碰撞中传递的动能越大;在 两种情况下,传递的动能相等。
两种情况下,传递的动能相等。
(2)完全非弹性碰撞上例中m1与m2发生完全非弹性碰撞,则有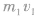
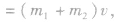 ,碰后的共同速度
,碰后的共同速度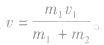
损失的动能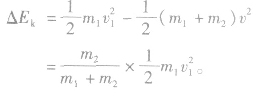
“二合一”模型:
这种模型是指两个速度不同的物体通过发生相互作用,最终两物体粘在一起运动或以共同的速度运动的模型。
这种模型的主要特征是终态共速(也可以是只在某一时刻共速.而研究的过程是从初始到共速的过程),从能量角度来看,这种过程中能量损失是最大的,属于完全非弹性碰撞的类型,在一维碰撞中的方程有: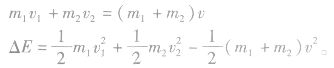
相互作用的两个物体在很多情况下皆可当成碰撞处理,那么对相互作用中两物体相距“恰最近”、相距 “恰最远”或“恰上升到最高点”等一类,临界问题,求解的关键都是“速度相等”。在“类碰撞”问题中,碰撞时间不一定很短,但遵守的规律却是相同的,例如下面几种情形。
(1)如图中,光滑水平面上的A物体以速度v0去撞击静止的B物体,A、B两物体相距最近时,两物体速度必定相等,此时弹簧最短,其压缩量最大,系统损失的动能等于弹簧获得的弹性势能, 
(2)在图中,物体A以速度v0滑到静止在光滑水平面上的小车B上,当A在B上滑行的距离最远时,A、B相对静止,A、B的速度必定相等,系统损失的动能等于AB间摩擦产生的热量。 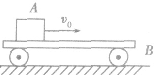
(3)在图中,子弹以速度v0射入静止在光滑的水平面上的木块中。当子弹不穿出时,子弹和木块的速度必定相等,系统损失的动能等于子弹与木块间摩擦产生的热量。 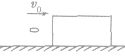
(4)如图所示,质量为M的滑块静止在光滑水平面上,滑块的光滑弧面底部与桌面相切,一个质量为m 的小球以速度v0向滑块滚来。设小球不能越过滑块,则小球到达滑块上的最高点时(即小球在竖直方向上的速度为零),两者的速度肯定相等(方向为水平向右),小球获得的重力势能等于系统损失的动能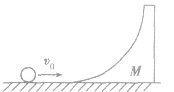
碰撞合理性的判断方法:
碰撞的合理性要遵循动量守恒定律、能量关系和速度关系:
1.系统动量守恒
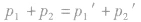
2.碰撞过程中系统的总动能不会增加
如果物体发生的是弹性碰撞,总动能不变;其他情况碰撞后会有部分动能转化为内能,系统的动能将减小。即 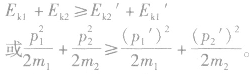
3.速度要符合情景如果碰前两物体同向运动,则后面物体的速度必大于前面物体的速度,即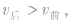 否则无法实现碰撞。碰撞后,原来在前的物体速度一定增大,且原来在前的物体速度大于或等于原来在后的物体速度,即
否则无法实现碰撞。碰撞后,原来在前的物体速度一定增大,且原来在前的物体速度大于或等于原来在后的物体速度,即
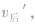 否则碰撞没有结束。如果碰前两物体是相向运动,则碰后,两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零。
否则碰撞没有结束。如果碰前两物体是相向运动,则碰后,两物体的运动方向不可能都不改变,除非两物体碰撞后速度均为零。
研究在弹性碰撞的过程中,相互作用的物体系统动量守恒。
实验原理:
一个质量较大的小球从斜槽滚下来,跟放在斜槽前边小支柱上另一质量较小的球发生碰撞后两小球都做平抛运动。由于两小球下落的高度相同,所以它们的飞行时间相等,这样如果用小球的飞行时间作时间单位,那么小球飞出的水平距离在数值上就等于它的水平速度。因此,只要分别测出两小球的质量m1、m2,和不放被碰小球时入射小球在空中飞出的水平距离s1,以及入射小球与被碰小球碰撞后在空中飞出的水平距离s1'和s2',若m1s1在实验误差允许范围内与m1s1'+m2s2'相等,就验证了两小球碰撞前后总动量守恒。
实验器材:
碰撞实验器(斜槽、重锤线),两个半径相等而质量不等的小球;白纸;复写纸;天平和砝码;刻度尺,游标卡尺(选用),圆规。
实验步骤:
1、用天平测出两个小球的质量m1、m2。
2、安装好实验装置,将斜槽固定在桌边,并使斜槽末端点的切线水平。
3、在水平地上铺一张白纸,白纸上铺放复写纸。
4、在白纸上记下重锤线所指的位置O,它表示入射球m1碰前的位置。
5、先不放被碰小球,让入射球从斜槽上同一高度处由静止开始滚下,重复10次,用圆规作尽可能小的圆把所有的小球落点圈在里面,圆心就是入射球不碰时的落地点的平均位置P。
6、把被碰球放在小支柱上,调节装置使两小球相碰时处于同一水平高度,确保入射球运动到轨道出口端时恰好与靶球接触而发生正碰。
7、再让入射小球从同一高度处由静止开始滚下,使两球发生正碰,重复10次,仿步骤(5)求出入射小球的落点的平均位置M和被碰小球落点的平均位置N。
8、过O、N作一直线,取OO'=2r(可用游标卡尺测出一个小球的直径,也可用刻度尺测出紧靠在一起的两小球球心间的距离),O'就是被碰小球碰撞时的球心竖直投影位置。
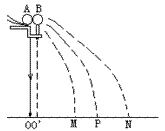
9、用刻度尺量出线段OM、OP、O'N的长度。
10、分别算出m1·
注意事项:
1、应使入射小球的质量大于被碰小球的质量。
2、要调节好实验装置,使固定在桌边的斜槽末端点的切线水平,小支柱与槽口间距离使其等于小球直径,而且两球相碰时处在同一高度,碰撞后的速度方向在同一直线上。
3、每次入射小球从槽上相同位置由静止滚下,可在斜槽上适当高度处固定一档板,使小球靠着挡板,然后释放小球。
4、白纸铺好后不能移动。
与“为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰...”考查相似的试题有:
- 质量为1kg的小球以4m/s的速度与质量为2kg的静止小球正碰,关于碰后的速度v1'和v2',下面哪些是可能正确的[ ]A.B.C.D.
- 两个氘核聚变产生一个中子和氦核(氦的同位素)。已知氘核的质量,氦核的质量,中子的质量。(1)写出聚变方程并计算释放的核...
- 光滑水平面上排列着三个等大的球心共线的弹性小球1,2,3,质量分别为m1,m2,m3。现给1号球一个水平速度v0,于是,1号球与2...
- (选修模块3-5)(15分)小题1:下列物理实验中,能说明粒子具有波动性的是 A.通过研究金属的遏止电压与入射光频率的关系,证明了...
- 甲、乙两个物体在同一直线上同向运动,甲物体在前、乙物体在后,甲物体质量为2kg,速度是1m/s,乙物体质量是4kg,速度是3m/s...
- 质量相等的甲乙两球在光滑水平面上沿同一直线运动。甲以7 kg·m/s的动量追上前方以5 kg·m/s的动量同向运动的乙球发生正碰,则...
- 太阳中含有大量的氘核,氘核不断发生核反应释放大量的核能,以光和热的形式向外辐射。已知氘核质量为2.0136 u,氦核质量为3.0...
- 为了验证碰撞中的动量是否守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同...
- 碰撞的恢复系数的定义为,其中v10和v20分别是碰撞前两物体的速度,v1和v2分别是碰撞后物体的速度。弹性碰撞的恢复系数e=1,非...
- 某同学用如图所示的(a)图装置通过半径相同的A、B两球的碰撞来探究碰撞中的守恒量,图中PQ是斜槽,QR为水平槽,实验时先使A...