本试题 “在2008北京奥运会上,俄罗斯著名撑杆跳运动员伊辛巴耶娃以5.05m的成绩第24次打破世界纪录.图为她在比赛中的几个画面.下列说法中正确的是( )A.运动员过最...” 主要考查您对功
机械能守恒定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 功
- 机械能守恒定律
功:
1、功的定义:力和作用在力的方向上通过的位移的乘积。是描述力对空间积累效应的物理量,是过程量。
2、功的两个必要因素:作用在物体上的力;物体在力的方向上发生的位移。
3、功的定义式:W=Fscosα,其中F是恒力,s是作用点的位移,α是力与位移间的夹角(功的单位焦耳,简称焦,符号J)。
4、功的计算
①恒力的功可根据W=FScosα进行计算,本公式只适用于恒力做功;
②根据W=P·t,计算一段时间内平均做功;
③利用动能定理计算力的功,特别是变力所做的功;
④根据功是能量转化的量度反过来可求功。
力做功情况的判定方法:
一个力对物体做不做功,是做正功还是做负功,判断的方法是:
(1)看力与位移之间的夹角,或者看力与速度之间的夹角:为锐角时,力对物体做正功;为钝角时,力对物体做负功;为直角时,力对物体不做功。
(2)看物体间是否有能量转化:若有能量转化,则必定有力做功。此方法常用于相连的物体做曲线运动的情况。
变力做功的求法:
公式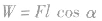 只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
只适用于求恒力做功,即做功过程中F的大小、方向始终不变。而实际问题中变力做功是常见的,如何解答变力做功问题是学习中的一个难点。不能机械地套用这一公式,必须根据有关物理规律通过变换或转化来求解。
1.用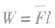 求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用
求变力做功如果物体受到的力方向不变,且大小随位移均匀变化,可用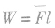 求变力F所做的功。其平均值大小 为
求变力F所做的功。其平均值大小 为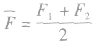 ,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
,其中F1是物体初态时受到的力的值,F2是物体末态时受到的力的值。如在求弹簧弹力所做的功时,再如题目中假定木桩、钉子等所受阻力与击入深度成正比的情况下,都可以用此法求解。
2.用微元法(或分段法)求变力做功变力做功时,可将整个过程分为几个微小的阶段,使力在每个阶段内不变,求出每个阶段内外力所做的功,然后再求和。当力的大小不变而方向始终与运动方向间的夹角恒定时,变力所做的功形: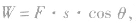 其中s是路程。
其中s是路程。
3.用等效法求变力做功若某一变力做的功等效于某一恒力做的功,则可以应用公式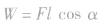 来求。这样,变力做功问题就转化为了恒力做功问题。
来求。这样,变力做功问题就转化为了恒力做功问题。
4.用图像法求变力做功存F—l图像中,图线与两坐标轴所围“面积”的代数和表示F做的功,“面积”有正负,在l轴上方的“面积”为正,在l轴下方的“面积”为负。
5.应用动能定理求变力做功
如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能变化量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
6.利用功能关系求变力做功
在变力做功的过程中,当有重力势能、弹性势能以及其他形式的能量参与转化时,可以考虑用功能关系求解。因为做功的过程就是能量转化的过程,并且转化过程中能量守恒。
7.利用W=Pt求变力做功
这是一种等效代换的观点,用W=Pt计算功时,必须满足变力的功率是恒定的。若功率P是变化的,则需用 计算,其中当P随时间均匀变化时,
计算,其中当P随时间均匀变化时, 。
。
1、内容:只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变。
2、表达式:
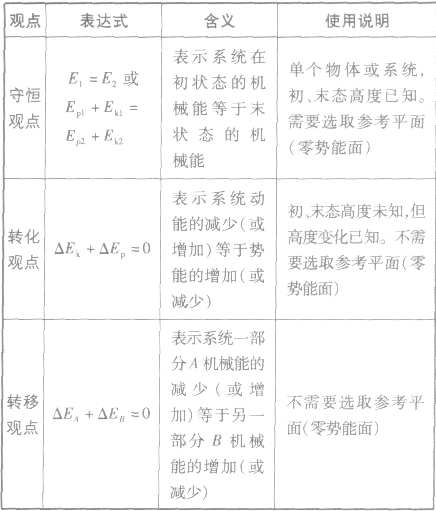
3.条件
机械能守恒的条件是:只有重力或弹力做功。可以从以下三个方面理解:
(1)只受重力作用,例如在不考虑空气阻力的情况下的各种抛体运动,物体的机械能守恒。
(2)受其他力,但其他力不做功,只有重力或弹力做功。例如物体沿光滑的曲面下滑,受重力、曲面的支持力的作用,但曲面的支持力不做功,物体的机械能守恒。
(3)其他力做功,但做功的代数和为零。
判定机械能守恒的方法:
(1)条件分析法:应用系统机械能守恒的条件进行分析。分析物体或系统的受力情况(包括内力和外力),明确各力做功的情况,若对物体或系统只有重力 (或弹力)做功,没有其他力做功或其他力做功的代数和为零,则系统的机械能守恒。
(2)能量转化分析法:从能量转化的角度进行分析:若只有系统内物体间动能和重力势能及弹性势能的相互转化,系统跟外界没有发生机械能的传递,机械能也没有转化成其他形式的能(如内能),则系统的机械能守恒。
(3)增减情况分析法:直接从机械能的各种形式的能量的增减情况进行分析。若系统的动能与势能均增加或均减少,则系统的机械能不守恒;若系统的动能不变,而势能发生了变化,或系统的势能不变,而动能发生了变化,则系统的机械能不守恒;若系统内各个物体的机械能均增加或均减少,则系统的机械能不守恒。
(4)对一些绳子突然绷紧、物体间非弹性碰撞等,除非题目特别说明,否则机械能必定不守恒。
竖直平面内圆周运动与机械能守恒问题的解法:
在自然界中,违背能量守恒的过程肯定是不能够发生的,而不违背能量守恒的过程也不一定能够发生,因为一个过程的进行要受到多种因素的制约,能量守恒只是这个过程发生的一个必要条件。如在竖直平面内的变速圆周运动模型中,无支撑物的情况下,物体要到达圆周的最高点,从能量角度来看,要求物体在最低点动能不小于最高点与最低点的重力势能差值。但只满足此条件物体并不一定能沿圆弧轨道运动到圆弧最高点。因为在沿圆弧轨道运动时还需满足动力学条件:所需向心力不小于重力,由此可以推知,在物体从圆弧轨道最低点开始运动时,若在动能全部转化为重力势能时所能上升的高度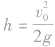 满足
满足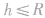 时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在
时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在 ,物体上升到圆周最高点时的速度
,物体上升到圆周最高点时的速度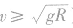 )时,物体可做完整的圆周运动;若在
)时,物体可做完整的圆周运动;若在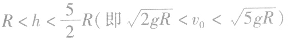 时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度
时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度 满足
满足 。故在解决这类问题时不能单从能量守恒的角度来考虑。
。故在解决这类问题时不能单从能量守恒的角度来考虑。
与“在2008北京奥运会上,俄罗斯著名撑杆跳运动员伊辛巴耶娃以5.0...”考查相似的试题有:
- 如图所示,一物体分别沿轨道和由静止滑下,物体与轨道间的动摩擦因数相同,若斜面保持静止,物体克服滑动摩擦力做的功分别为...
- 一根长为L、质量为m的均匀链条放在光滑的水平桌面上,其长度的一半悬于桌边,若要将悬着的部分拉回桌面,至少做功[ ]A.mgLB.m...
- 下列是一些说法中,正确的是( )A.一质点受两个力作用且处于平衡状态(静止或匀速),这两个力在同一段时间内的冲量一定相同;...
- 如图所示:小车沿倾角为θ的光滑斜面滑下,在小车的水平台面上有一质量为M的木块和小车保持相对静止,则( )A.小车下滑时木...
- 如图所示,木块A放在木板B的左端,用恒力F将A拉至B的右端,第一次将B固定在地面上,F做功为W1,生热为Q1;第二次让B在光滑地...
- 一个质量的物体自由下落,重力加速度取,则第内重力的平均功率是:( )A.;B.;C.;D.。
- 下列有关力做功的说法,正确的是( )A.静摩擦力对物体一定不做功B.滑动摩擦力对物体可以做正功C.卫星绕地球做匀速圆周运...
- 如图所示,水平面上固定一轨道,轨道所在平面与水平面垂直,其中bcd是一段以O为圆心、半径为R的圆弧,c为最高点,弯曲段abcde...
- 如图所示,斜面置于光滑水平地面上,其光滑斜面上有一物体由静止沿斜面下滑,在物体下滑过程中,下列说法正确的是A.物体的重...
- 利用气垫导轨验证机械能守恒定律,实验装置如图所示,水平桌面上固定一倾斜的气垫导轨;导轨上A点处有一带长方形遮光片的滑块...