本试题 “(1)A、B为同一波源发出的两列波,某时刻在不同介质、相同距离上的波形如图所示,则两列波的波速之比vA:vB是______________;A.1:3B.1:2C.2:1D.3:1...” 主要考查您对波的图像
光的折射定律
全反射,临界角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 波的图像
- 光的折射定律
- 全反射,临界角
波动图像:
1.概念:表示波的传播方向上,介质中的各个质点在同一时刻相对平衡位置的位移。
2.意义:波在传播过程中各质点在某时刻的位移情况
3.特点:
①波形图线是正弦或余弦曲线的波称为简谐波。简谐波是最简单的波。对于简谐波而言,各个质点振动的最大位移都相同
②波的图像的重复性:相隔时间为周期整数倍的两个时刻的波形相同
③波的传播方向的双向性:不指定波的传播方向时,图像中波可能向x轴正向或x轴负向传播
4.应用特点:
(1)从图像上直接读出波长和振幅。
(2)可确定任一质点在该时刻的位移。
(3)可确定任一质点在该时刻的加速度方向。
(4)若知道波速v的方向,可知各质点的运动方向。
(5)若知道该时刻某质点的运动方向,可判断波的传播方向。
(6)若已知波速v的大小,可求频率f或周期T:
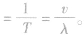
(7)若已知f或T,可求v的大小: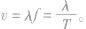
(8)若已知波速v的大小和方向,可画出在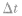 前后的波形图,即波沿着(或逆着)传播方向平移
前后的波形图,即波沿着(或逆着)传播方向平移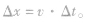
(9)结合波的图像,可确定任一质点的振动图像
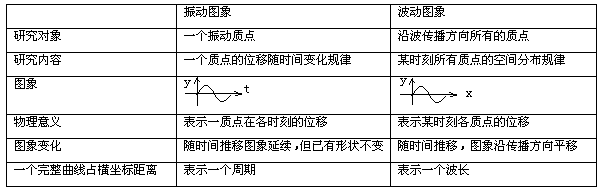
波动图像与振动图像的比较:
已知波速v和波形,画出再经△t时间波形图的方法:
1.特殊点法
在波形图上找两特殊点,如过平衡位置的点和与它相邻的峰(符)点,先确定这两点的振动方向,再看 。由于经nT时间波形不变,所以采取去整nT留零t的方法,分别作出两特殊点经t时间后的位置,然后按正弦规律画出新波形图。
。由于经nT时间波形不变,所以采取去整nT留零t的方法,分别作出两特殊点经t时间后的位置,然后按正弦规律画出新波形图。
2.平移法一——移波形
先算出经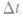 时间波传播的距离
时间波传播的距离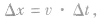 ,再把波形沿波的传播方向平移
,再把波形沿波的传播方向平移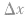 即可。因为波动图像的重复性,若已知波长λ,则波形平移n个λ时波形不变。当
即可。因为波动图像的重复性,若已知波长λ,则波形平移n个λ时波形不变。当 时,可采取去整
时,可采取去整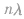 留零x的方法,只需平移x即可。
留零x的方法,只需平移x即可。
3.平移法二——移坐标轴
计算方法同上,将坐标轴y逆着波的传播方向平移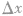 即可.
即可.
已知两不同时刻波动图像类问题的解法:
如图所示,已知某简谐波在t与t+△t时刻的波形图,从图上可以确定该波的波长λ、振幅A。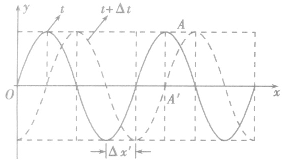
在求解波的周期、波速时有两种方法:
(1)传播的观点
由波形图可知,波在△t时间内传播的距离为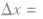
 (波沿x轴正向传}
(波沿x轴正向传}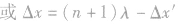 (波沿x轴负向传播)时,则波速
(波沿x轴负向传播)时,则波速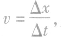 周期
周期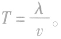
(2)振动观点
在波形图中取某一质点,比较该质点(如图中A) 在两时刻的位置和状态,确定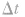 与周期的关系,如在图中,波向右传播时
与周期的关系,如在图中,波向右传播时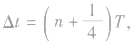 波向左传播时,
波向左传播时,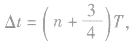 ,可求得周期的表达式,再由
,可求得周期的表达式,再由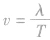 可求得波速。在这类题目中,同时应注意对时间的限制,当
可求得波速。在这类题目中,同时应注意对时间的限制,当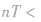
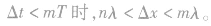
振动图像与波动图像相结合问题的解法:
解决两种图像相结合问题的基本思路
(1)首先识别哪一个是波动图像,哪一个是振动图像,两者间的联系纽带是周期与振幅。
(2)然后确定振动图像对应于波动图像中的哪一个质点,波动图像对应于振动图像中的哪一个时刻。
(3)再从振动图像中找出该质点在波动图像中的那一时刻的振动方向,然后再确定波的传播方向及其他问题。
波动图像中多解性问题的解法:
波动图像问题中的多解性涉及:
(1)波的空间周期性;
(2)波的时间周期性;
(3)波的双向性;
(4)波的对称性;
(5)介质中两质点间的距离与波长关系未定;
(6)介质中质点的振动方向未定。具体讨论如下:
①波的空间周期性
沿波的传播方向,在x轴上任取一点P(x),如图所示。P点的振动完全重复波源O点的振动,只是时间上比O点要落后出时间,且 在同一列波上,凡坐标与P点坐标x之差为波长整数倍的质点,在同一时刻t的振动位移都与坐标为x的质点的振动位移相同,其振动速度、加速度也都与坐标为x的质点相同,或者说它们的振动“相貌”完全相同。因此在同一列波上,某一振动“相貌”势必会不断地重复出现,这就是机械波的空间周期性。波的空间周期性说明,在同一列波上,相距为波长整数倍的多个质点的振动情况完全相同。
在同一列波上,凡坐标与P点坐标x之差为波长整数倍的质点,在同一时刻t的振动位移都与坐标为x的质点的振动位移相同,其振动速度、加速度也都与坐标为x的质点相同,或者说它们的振动“相貌”完全相同。因此在同一列波上,某一振动“相貌”势必会不断地重复出现,这就是机械波的空间周期性。波的空间周期性说明,在同一列波上,相距为波长整数倍的多个质点的振动情况完全相同。 
②波的时间周期性
在x轴上取一给定质点,在t+kT时刻的振动情况与它在t时刻的振动情况(位移、速度、加速度等)相同。因此在t时刻的波形,在t+kT时刻必然多次重复出现,这就是机械波的时间周期性。
波的时间周期性表明,波在传播过程中,经过整数倍周期时,其波形图线相同。
③波的双向性
双向性是指波沿正、负两方向传播时,若沿正、负两方向传播的时间之和等于周期的整数倍,则沿正、负两方向传播到那一时刻的波形图相同。
④波的对称性
波源的振动,要带动它左、右相邻质点的振动,波要向左、右两方向传播。对称性是指波在向左、右同时传播时,关于波源对称的左、右两质点的振动情况完全相同。
⑤介质中两质点间的距离与波长关系未定
在波的传播方向上,如果两个质点间的距离不确定,就会形成多解,学生若不能联想到所有可能的情况,则易出现漏解。
⑥介质中质点的振动方向未定
在波的传播过程中,质点振动方向与传播方向相联系,若某一质点振动方向未确定,则波的传播方向有两种,这样会形成多解。
光的折射定律:
1、光的折射现象:光由一种介质射入另一种介质时,在两种介质的界面上将发生光的传播方向改变的现象叫光的折射。
2、光的折射定律:折射光线、入射光线和法线在同一平面内,折射光线和入射光线分居于法线两侧;入射角的正弦跟折射角的正弦成正比。
3、在折射现象中,光路是可逆的。
折射成像作图法:
1.折射成像画法应用折射定律,确定物点发出的任意两条入射光线的折射光线,即可找到折射所成的像。如图所示。
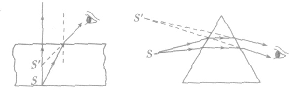
2.四点提示
(1)光线实际是从哪个物体发出的;
(2)是从光密介质射向光疏介质还是从光疏介质射向光密介质;
(3)必要的时候还需要借助光的可逆性原理;
(4)注意作图时一定要规范,光线与法线、光线的反向延长线要用实线和虚线区分。
光密介质与光疏介质:
1.定义:两种介质相比较,折射率较大的介质叫做光密介质,折射率较小的介质叫做光疏介质
2.特点:
(1)光由光疏介质射人光密介质时,折射角小于入射角;光由光密介质射入光疏介质时,折射角大于入射角。
(2)光在光疏介质中的传播速度大于在光密介质中的传播速度。
(3)光密介质与光疏介质是相对而言的。单独一种介质无法确定它是光密介质还是光疏介质
全反射:
1.定义:光从光密介质射人光疏介质时,折射角大于入射角,当入射角增大到某一角度时,折射角达到90。,折射光完全消失,只剩下反射光,这种现象叫做全反射
2.临界角:
①定义:折射角为90。时的入射角叫做全反射的临界角。
②公式:光由折射率为n的介质射入空气 (真空)时,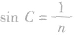
3.条件:
①光由光密介质射向光疏介质
②入射角等于或大于临界角
全反射的计算方法:
光从一种介质射入另一种介质时一般都要同时发生反射与折射现象,如图所示。当光线从光密介质射向光疏介质时,折射角大于入射角。这样就有可能在入射角还没有增大到90。以前,折射角就已经达到90。,以光从水射人空气为例,当入射角增大到某一数值C 时,折射光线恰好掠过水面,和界面平行,折射角等于90。,再继续增大入射角,光线全部反射回水中,不再有折射光线进入空气中,于是形成光的全反射现象。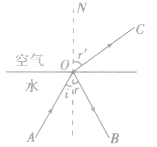
当折射角为90。时的入射角C叫做临界角,可见发生全反射的条件是:
①光线从光密介质射入光疏介质。
②入射角≥临界角(C),对于临界角有: 。
。
分析光的全反射、临界角问题的一般思路:
(1)画出恰好发生全反射的光路。
(2)利用几何知识分析边、角关系,找出临界角。
(3)以刚好发生全反射的光线为比较对象来判断光线是否发生全反射,从而画出其他光线的光路图。
物质的密度与光密介质、光疏介质:
光密介质和光疏介质是相对的,是根据介质对同种频率的光的折射率大小来划分的。折射率较小的称为光疏介质,折射率较大的称为光密介质。显然对同一介质来说,当与其对比的介质不同时,它可能属于光密介质,也可能属于光疏介质,如水相对于空气是光密介质,但相对于玻璃就属于光疏介质了,对于某种介质,没有与之相对比的其他介质时,谈论它是光密介质还是光疏介质是无意义的。而物质的密度与介质的折射率之间没有直接的联系,密度大的介质折射率不一定大,如酒精的密度小于水的密度,但酒精的折射率大于水的折射率。但对于同种物质来说,当其密度变大时,通常折射率也变大。如空气,在海边、靠近海平面的空气温度低,密度大,折射率也大,常引起“海市蜃楼”现象;在沙漠,靠近地面的空气温度高,密度小,折射率也小,这正是引起“沙漠蜃景”的原因。
与“(1)A、B为同一波源发出的两列波,某时刻在不同介质、相同距...”考查相似的试题有:
- 如图所示为某一时刻简谐横波的图象,波的传播方向沿+x方向,下列说法中正确的是[ ]A.此时刻质点C的振幅为负值B.此时刻质点B...
- 一列简谐波在t=0时刻的波形图如图12-2-8(a)所示,图(b)表示该波传播的介质中某质点此后一段时间内的振动图象,则( )图12-...
- 坐标原点O处有一波源在t=0时刻开始做简谐运动,形成简谐横波沿x轴传播。当t=2s时,在x=-7.7m处的质点p及附近的点第一次出现...
- 细绳上有一列波,沿着绳子向左传播,A、B是细绳上的两点,它们的平衡位置间的距离小于一个波长,当A点振动到最高点时,B点恰...
- 一束黄光从介质a射向介质b,在a、b介质的分界面上发生了全反射,则下列说法正确的是A.a是光疏介质,b是光密介质B.黄光在介...
- 半圆柱透镜的截面如图所示,圆心为O,半径OA=R.一束光从半径OA的中点垂直于界面射入透镜后,从圆孤面射出时出射光线相对于入...
- 如图所示,一细束红蓝复色光与AB边垂直射入直角三棱镜,在AC面上反射和折射后分成两束细光束,其中一束细光束为单色光,若用v...
- 华裔科学家高锟因在“有关光导纤维用于光学通信方面”取得了突破性成就而获得2009年诺贝尔物理学奖.利用光导纤维进行光学通信...
- 如图所示为一直角棱镜的横截面,∠bac=90°,∠abc=60°,O点是bc的中点。一平行细光束从O、c之间(不含O、c两点)的P点沿垂直...
- 华裔科学家高锟获得2009年诺贝尔物理奖,他被誉为“光纤通讯之父”. 光纤通讯中信号传播的主要载体是光导纤维,它的结构如图所...