本试题 “在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.(1)为了能较准确地描绘运动轨迹,下面列出一些操作要求,将你认...” 主要考查您对实验:研究平抛运动
力的合成
力的分解
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 实验:研究平抛运动
- 力的合成
- 力的分解
平抛运动实验:
(1)实验目的:
1、用实验方法描出平抛物体的运动轨迹。
2、从实验轨迹求平抛物体的初速度。
(2)实验原理:
平抛物体的运动可以看作是两个分运动的合运动:一是水平方向的匀速直线运动,另一个是竖直方向的自由落体运动。令小球做平抛运动,利用描迹法描出小球的运动轨迹,即小球做平抛运动的曲线,建立坐标系,测出曲线上的某一点的坐标x和y,根据重力加速度g的数值,利用公式y=![]() gt2求出小球的飞行时间t,再利用公式x=vt,求出小球的水平分速度,即为小球做平抛运动的初速度。
gt2求出小球的飞行时间t,再利用公式x=vt,求出小球的水平分速度,即为小球做平抛运动的初速度。
(3)实验器材:
斜槽,竖直固定在铁架台上的木板,白纸,图钉,小球,有孔的卡片,刻度尺,重锤线。
(4)实验步骤:
1、安装调整斜槽:用图钉把白纸钉在竖直板上,在木板的左上角固定斜槽,可用平衡法调整斜槽,即将小球轻放在斜槽平直部分的末端处,能使小球在平直轨道上的任意位置静止,就表明水平已调好;
2、调整木板:用悬挂在槽口的重锤线把木板调整到竖直方向,并使木板平面与小球下落的竖直面平行。然后把重锤线方向记录到钉在木板的白纸上,固定木板,使在重复实验的过程中,木板与斜槽的相对位置保持不变;
3、确定坐标原点O:把小球放在槽口处,用铅笔记下球在槽口时球心在图板上的水平投影点O,O点即为坐标原点;
4、描绘运动轨迹:在木板的平面上用手按住卡片,使卡片上有孔的一面保持水平,调整卡片的位置,使从槽上滚下的小球正好穿过卡片的孔,而不擦碰孔的边缘,然后用铅笔在卡片缺口上点个黑点,这就在白纸上记下了小球穿过孔时球心所对应的位置。保证小球每次从槽上开始滚下的位置都相同,用同样的方法,可找出小球平抛轨迹上的一系列位置。取下白纸用平滑的曲线把这些位置连接起来即得小球做平抛运动的轨迹;
5、计算初速度:以O点为原点画出竖直向下的y轴和水平向右的x轴,并在曲线上选取A、B、C、D、E、F六个不同的点,用刻度尺和三角板测出它们的坐标x和y,用公式x=v0t和y=![]() gt2计算出小球的初速度v0,最后计算出v0的平均值,并将有关数据记入表格内。
gt2计算出小球的初速度v0,最后计算出v0的平均值,并将有关数据记入表格内。
(5)注意事项:
1、实验中必须保持通过斜槽末端点的切线水平,方木板必须处在竖直面内且与小球运动轨迹所在的竖直平面平行,并使小球的运动靠近图板但不接触。
2、小球必须每次从斜槽上同一位置滚下。
3、坐标原点(小球做平抛运动的起点)不是槽口的端点,应是小球在槽口时,球的球心在木板上的水平投影点。
4、要在平抛轨道上选取距O点远些的点来计算球的初速度,这样可使结果的误差较小。
当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的效果跟原来几个力的共同效果相同,这个力就叫做那几个力的合力,原来的几个力叫做这个力的分力。
①合力与分力是针对同一受力物体而言的。
②一个力之所以是其他几个力的合力,或者其他几个力之所以是这个力的分力,是冈为这一个力的作用效果与其他几个力共同作用的效果相当,合力与分力之间的关系是一种等效替代的关系。
③合力可能大于任何一个分力,也可能小于任何一个分力,也可能介于两个分力之间。
④如果两个分力的大小不变,夹角越大,合力就越小;夹角越小,合力就越大。
⑤两个大小一定的力F1、F2,其合力的大小范围
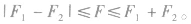

力的运算法则:
1.平行四边形定则
作用在同一点的两个互成角度的力的合力,不等于两分力的代数和,而是遵循平行四边形定则。如果以表示两个共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用这两个邻边之间的对角线表示,这叫做力的平行四边形定则,如图所示。 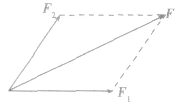
2.三角形定则和多边形定则如图(a)所示,两力F1、F2合成为F的平行四边形定则,可演变为(b)图,我们将(b)图称为三角形定则合成图,即将两分力F1、F2首尾相接,则F就是由F,的尾端指向F2的首端的有向线段所表示的力。
如果是多个力合成,则由三角形定则合成推广可得到多边形定则,如图为三个力F1,F2、F3的合成图,F 为其合力。
(1)定义:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
(2)力的合成与分解的具体方法
a.作图法:选取统一标度,严格作出力的图示及平行四边形,然后用统一标度去度量各个力的大小;
b.计算法:根据平行四边形定则作出示意图,然后利用解三角形的方法求合力或分力的大小。一般要求会解直角三角形。
力的分解的几种情况:
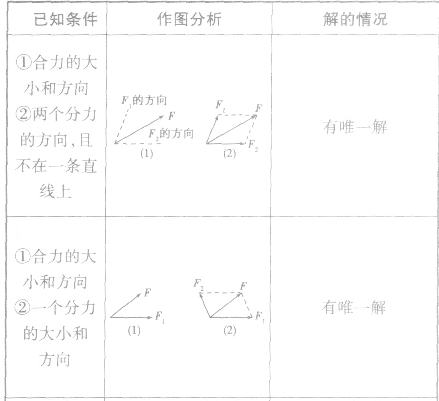
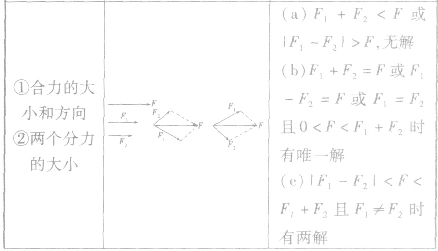
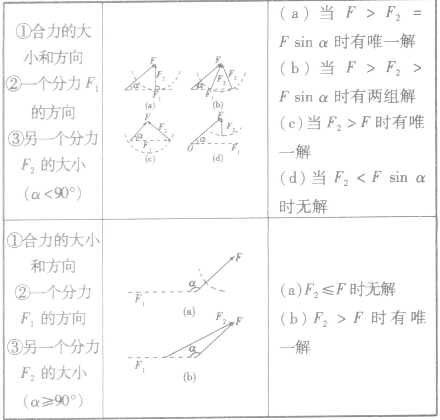
分解方法:
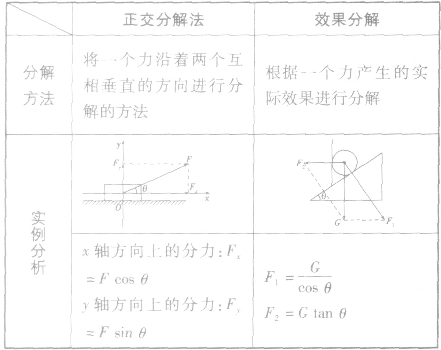
几种按效果分解的实例:


由力的三角形定则求力的最小值:
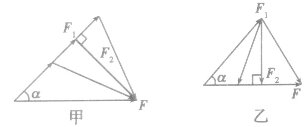
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2最小的条件是:两个分力垂直,如图甲。最小值
 。
。 (2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙。最小值
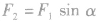 。
。
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力 F同方向。最小值
 。
。由圆的切线求力方向的极值:
(1)当已知两分力F1、F2的大小时,合力,的方向与较大分力间夹角有最大值,与较小分力间夹角有最小值。如图所示,设两分力中F1较大,则合力F与F1之间最大夹角θ满足
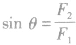 。
。 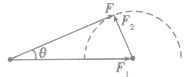
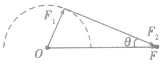
(2)当已知合力F与其中一个分力F1的大小时,若F >F1,则另一个分力F2与合力F的方向间夹角有一最大值。如图所示,其最大夹角θ满足
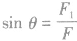 。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足
。若F<F1时,则另一个分力F2与合力F间夹角无极值,可在0。~180。之间变化:当F1与F同向时分力F2与合力F之间夹角最大,为180。;当F1与F反向时分力F2与合力 F之间夹角最小,为0。,但两分力间夹角有最大值,其最大值满足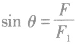 。
。
与“在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过...”考查相似的试题有:
- 某物理兴趣小组采用如图所示的装置深入研究平抛运动.质量分别为mA和mB的A、B小球处于同一高度,M为A球中心初始时在水平地面...
- 一物体受到三个共点力的作用,它们的大小分别为F1=3N、F2=5N、F3=10N,则它们的合力大小不可能是[ ]A.1NB.3NC.7ND.13N
- 如图所示,物体M在竖直向上的拉力F的作用下能静止在斜面上,关于M受力的个数,下列说法中正确的是( ) A.M一定是受两个力作...
- 如图,OP为粗糙的水平杆,OQ为光滑的竖直杆,质量相同的两个小环a、b,通过细线连接套在杆上,a环在A位置时平衡.当a环移到位...
- 光滑水平面上,一个质量为0.5kg的物体从静止开始受水平力而运动,在前5s内受到一个正东方向、大小为1N的水平恒力作用,第5s末...
- 如图所示是骨折病人的牵引装置示意图,绳的一端固定,绕过定滑轮和动滑轮后挂着一个重物,与动滑轮的帆布带拉着病人的脚,整...
- F1、F2合力方向竖直向下,若保持F1的大小和方向都不变,保持F2的大小不变,而将F2的方向在竖直平面内转过60°角,合力的方向仍...
- 如图所示,物体A放在物体B上,物体B放在光滑水平面上,已知mA=6kg,mB=2kg,A、B间动摩擦因数μ=0.2.现对A物体施加一个水平向...
- 将一只苹果斜向上抛出,苹果在空中依次飞过三个完全相同的窗户1、2、3.图中曲线为苹果在空中运行的轨迹.若不计空气阻力的影...
- 三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们悬挂一重物,如图所示,其中OB是水平的,A、B端固定,若逐渐增加C端...