本试题 “两个行星的质量分别为m1和m2,绕太阳运动的轨道半径分别为r1和r2,求:(1)它们与太阳间的引力之比;(2)它们的公转周期之比。” 主要考查您对开普勒行星运动定律
万有引力定律
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 开普勒行星运动定律
- 万有引力定律
开普勒行星运动定律:
1、所有行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
2、对每个行星而言太阳和行星的连线在相等的时间内扫过相同的面积。
3、所有行星轨道的半长轴R的三次方与公转周期T的二次方的比值都相同,即![]() 常量。
常量。
4、常用开普勒三定律来分析行星在近日点和远日点运动速率的大小。
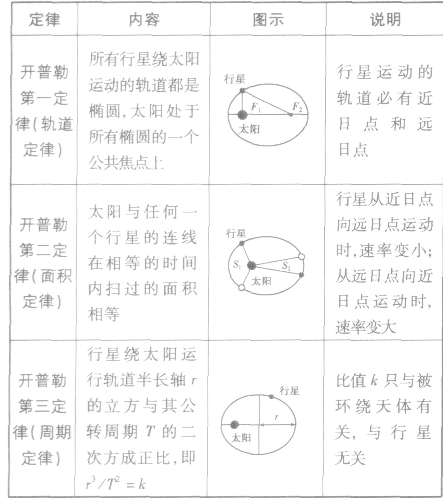
开普勒三定律的对比:
开普勒第一定律:
开普勒第一定律,也称轨道定律:每一个行星都沿各自的椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点。
开普勒第二定律:
开普勒第二定律,也称面积定律:在相等时间内,太阳和运动中的行星的连线(向量半径)所扫过的面积都是相等的。这一定律实际揭示了行星绕太阳公转的角动量守恒。(角动量在高中学习中不考查)
开普勒第三定律:
开普勒第三定律,也称周期定律:是指绕以太阳为焦点的椭圆轨道运行的所有行星,其椭圆轨道半长轴的立方与周期的平方之比是一个常量。
知识点拨:
近年高考试题中的天体运动问题,试题情境熟悉,多为匀速圆周运动模型,不是卫星环绕地球的圆周运动,就是行星环绕太阳的圆周运动。运算简单,大多数试题直接运用开普勒第三定律进行分析或计算,有些试题则需运用牛顿第二定律与万有引力定律、“黄金代换”等分析计算。
万有引力定律:
1、内容:宇宙间的一切物体都是互相吸引的。两个物体间的引力的大小,跟它们的质量的乘积成正比,跟它们的距离的平方成反比。
2、表达式: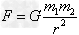 ,G=6.67×10-11 N·m2/kg2。
,G=6.67×10-11 N·m2/kg2。
3、适用条件:适用于相距很远,可以看做质点的两物体间的相互作用,质量分布均匀的球体也可用此公式计算,其中r指球心间的距离。
重力和万有引力的关系:
物体重力是地球引力的一个分力。如图,万有引力F的另一个分力F1是使物体随地球做匀速圆周运动所需的向心力。越靠近赤道(纬度越低),物体绕地轴运动的向心力F1就越大,重力就越小;反之,纬度越高(靠近地球两极),物体绕地轴随地球一起运动的向心力F1就越小,重力就越大。在两极,重力等于万有引力;在赤道,万有引力等于重力加上向心力。
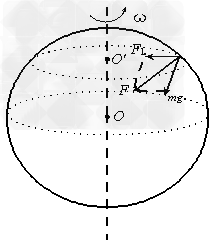
①物体的重力随地面高度h的变化情况:物体的重力近似地球对物体的吸引力,即近似等于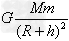 ,可见物体的重力随h的增大而减小,由G=mg得g随h的增大而减小。
,可见物体的重力随h的增大而减小,由G=mg得g随h的增大而减小。
②在地球表面(忽略地球自转影响):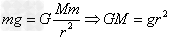 (g为地球表面重力加速度,r为地球半径)。
(g为地球表面重力加速度,r为地球半径)。
③当物体位于地面以下时,所受重力也比地面要小,物体越接近地心,重力越小,物体在地心时,其重力为零。
1、内容:宇宙间的一切物体都是互相吸引的。两个物体间的引力的大小,跟它们的质量的乘积成正比,跟它们的距离的平方成反比。
2、表达式:
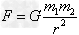 ,G=6.67×10-11 N·m2/kg2。
,G=6.67×10-11 N·m2/kg2。3、适用条件:适用于相距很远,可以看做质点的两物体间的相互作用,质量分布均匀的球体也可用此公式计算,其中r指球心间的距离。
重力和万有引力的关系:
物体重力是地球引力的一个分力。如图,万有引力F的另一个分力F1是使物体随地球做匀速圆周运动所需的向心力。越靠近赤道(纬度越低),物体绕地轴运动的向心力F1就越大,重力就越小;反之,纬度越高(靠近地球两极),物体绕地轴随地球一起运动的向心力F1就越小,重力就越大。在两极,重力等于万有引力;在赤道,万有引力等于重力加上向心力。

①物体的重力随地面高度h的变化情况:物体的重力近似地球对物体的吸引力,即近似等于
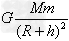 ,可见物体的重力随h的增大而减小,由G=mg得g随h的增大而减小。
,可见物体的重力随h的增大而减小,由G=mg得g随h的增大而减小。②在地球表面(忽略地球自转影响):
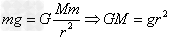 (g为地球表面重力加速度,r为地球半径)。
(g为地球表面重力加速度,r为地球半径)。③当物体位于地面以下时,所受重力也比地面要小,物体越接近地心,重力越小,物体在地心时,其重力为零。
开普勒行星运动定律:
发现相似题
与“两个行星的质量分别为m1和m2,绕太阳运动的轨道半径分别为r1...”考查相似的试题有:
- 已知地球半径为R,月球半径为r,地球与月球之间的距离(两球中心之间的距离)为L。月球绕地球公转的周期为T1,地球自转的周期...
- 发射月球探测器存在发射“窗口”,所谓“窗口”既是探测器进入奔月轨道(图中的轨道4)的时刻。为避免错过发射“窗口”,我国的“嫦...
- 两行星A和B是两均匀球体,行星A的卫星A沿圆轨道运行的周期为Ta,行星B的卫星B沿圆轨道运行的周期为Tb.设两卫星均为各自中心星...
- 月球环绕地球运动的轨道半径约为地球半径的60倍,其运行周期约为27天.现应用开普勒定律计算:在赤道平面内离地面多高时,人...
- 一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量...
- (9分).欧盟和我国合作的“伽利略”全球卫星定位系统的空间部分由平均分布在三个轨道平面上的30颗轨道卫星构成,每个轨道平面...
- 1969年7月16日9时,阿波罗11号飞船飞船在美国卡拉维拉尔角点火升空,拉开人类登月这一伟大历史事件的帷幕。7月20日下午在月面...
- 设行星绕恒星运动轨道为圆形,则它运动的轨道半径的三次方与周期平方之比R3/T2=K为常数,此常数的大小:( )A.只与恒星有...
- 北斗卫星导航系统是我国自行研制开发的区域性三维卫星定位与通信系统(CNSS),建成后的北斗卫星导航系统包括5颗同步卫星和30颗...
- 同步卫星A的运行速率为v1,向心加速度为a1,运转周期为T1;放在地球赤道上的物体B随地球自转的线速度为v2,向心加速度为a2,...