本试题 “A.(选修模块3-3)(1)下列说法正确的是______A.显微镜下看到墨水中的炭粒的无规则运动是热运动B.一定量100℃的水变成100℃的水蒸汽,其分子之间的势能增加...” 主要考查您对动量守恒定律
阿伏伽德罗常数
理想气体状态方程
氢原子的能级
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 动量守恒定律
- 阿伏伽德罗常数
- 理想气体状态方程
- 氢原子的能级
1、内容:一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变。
2、表达式:m1v1+m2v2=m1v1'+m2v2'。
3、动量守恒定律成立的条件:
①系统不受外力或系统所受外力的合力为零;
②系统所受的外力的合力虽不为零,但系统外力比内力小得多,如碰撞问题中的摩擦力,爆炸过程中的重力等外力比起相互作用的内力来小得多,可以忽略不计;
③系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变。
4、动量守恒的速度具有“四性”:
①矢量性;②瞬时性;③相对性;④普适性。
动量守恒定律与机械能守恒定律的比较:



系统动量守恒的判断方法:
方法一:南动量守恒的条件判断动量守恒的步骤如下:
(1)明确系统由哪几部分组成。
(2)对系统中各物体进行受力分析,分清哪些是内力,哪些是外力。
(3)看所有外力的合力是否为零,或内力是否远大于外力,从而判断系统的动量是否守恒。
方法二:南系统动量变化情况判断动量守恒方法如下:
(1)明确初始状态系统的总动量是多少。
(2)对系统内的物体进行受力分析、运动分析,确定每一个物体的动量变化情况。
(3)确定系统动量变化情况,进而判定系统的动量是否守恒。
阿伏加德罗常量:
摩尔的任何物质含有的微粒数都相同,这个数的测量值NA=6.02×1023 mol-1。是联系微观世界和宏观世界的桥梁。它把物质的摩尔质量、摩尔体积这些宏观物理量和分子质量、分子体积这些微观物理量联系起来了。
1.表述:一定质量气体的状态变化时,其压强和体积的乘积与热力学温度的比是个常数.
2.表达式:
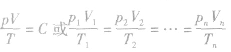
这个常数C由气体的种类与气体的质量决定,或者说这个常数由物质的量决定,与其他参量无关
3.适用条件:质量一定、理想气体
4.与实验定律的关系:
气体的三个实验定律是理想气体状态方程的特例:
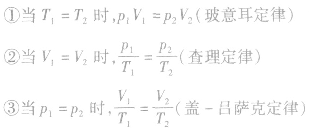
5.两个推论:
(1)密度方程:
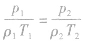
上式与气体的质量无关,即不要求质量恒定
(2)道尔顿分压定律:
一定质量的气体分成n份(或将n份气体合为一份)时
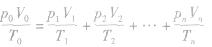
此式要求气体的质量不变,即前后总质量相同
活塞类问题的解法:
1.一般思路
(1)分析题意,确定对象:热学研究对象(一定质量的气体);力学研究对象(活塞、缸体或系统)。
(2)分析物理过程,对热学对象依据气体实验定律列方程;对力学对象依据牛顿运动定律列方程。
(3)挖掘隐含条件,列辅助方程。
(4)联立求解,检验结果。
2.常见类型
(1)系统处于力学的平衡状态,综合利用气体实验定律和平衡方程求解。
(2)系统处于力学的非平衡状态,综合利用气体实验定律和牛顿运动定律求解。
(3)容器与封闭气体相互作用满足守恒定律的条件(如动量守恒、能量守恒、质量守恒等)时,可联立相应的守恒方程求解。
(4)多个相互关联的气缸分别密闭几部分气体时,可分别研究各部分气体,找出它们各自遵循的规律,列出相应的气体状态方程,再列出各部分气体压强之间及体积之问的关系式,联立求解。
变质量气体问题的处理方法:
气体三定律与气体的状态方程都强调“一定质量的某种气体”,即气体状态变化时,气体的质量不能变。用气体三定律与气体状态方程研究变质量气体问题时有多种不同的处理方法。
(1)口袋法:给初状态或者末状态补接一个口袋,把变化的气体用口袋收集起来,从而保证质量不变。
(2)隔离法:对变化部分和不变部分隔离.只对不变部分进行研究,从而实现被研究的气体质量不变。
(3)比较常数法:气体常数与气体质量有关,质量变化,气体常数变化;质量不变,气体常数不变。根据各个状态的已知状态参量计算出各个状态下的气体常数C,然后进行比较。
(4)利用推论法:气体的密度方程不要求质量恒定,可由此得到相应状态的密度,再结合体积等解决问题。也可利用分压定律来研究变质量气体的问题。具体来说,有以下四种典型的情景,可以通过选择适当的对象化变质量为定质量:
①充气问题
向球、轮胎中充气是一个典型的气体变质量问题,只要选择球内原有气体和即将打入的气体作为研究对象,就可把充气过程中的气体质量变化问题转化为定质量气体的状态变化问题。
②抽气问题
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体看成整体来作为研究对象,质量不变,抽气过程中的气体可看成是等温膨胀过程。
③灌气问题
将一个大容器里的气体分装到多个小容器中的问题也是一个典型的变质量问题。分析这类问题时,可以把大容器中的气体和多个小容器中的气体看成整体来作为研究对象,将变质量问题转化为定质量问题。
④漏气问题
容器漏气过程中气体的质量不断发生变化,属于变质量问题,不能用理想气体状态方程求解。如果选容器内剩余气体为研究对象,便可使问题变成一定质量的气体状态变化,可用理想气体状态方程求解。
氢原子的能级:
1、氢原子的能级图 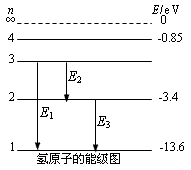
2、光子的发射和吸收
①原子处于基态时最稳定,处于较高能级时会自发地向低能级跃迁,经过一次或几次跃迁到达基态,跃迁时以光子的形式放出能量。
②原子在始末两个能级Em和En(m>n)间跃迁时发射光子的频率为ν,其大小可由下式决定:hυ=Em-En。
③如果原子吸收一定频率的光子,原子得到能量后则从低能级向高能级跃迁。
④原子处于第n能级时,可能观测到的不同波长种类N为:![]() 。
。
⑤原子的能量包括电子的动能和电势能(电势能为电子和原子共有)即:原子的能量En=EKn+EPn。轨道越低,电子的动能越大,但势能更小,原子的能量变小。
电子的动能:![]() ,r越小,EK越大。
,r越小,EK越大。
氢原子的能级及相关物理量:
在氢原子中,电子围绕原子核运动,如将电子的运动看做轨道半径为r的圆周运动,则原子核与电子之间的库仑力提供电子做匀速圆周运动所需的向心力,那么由库仑定律和牛顿第二定律,有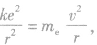 ,则
,则
①电子运动速率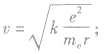
②电子的动能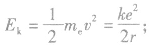
③电子运动周期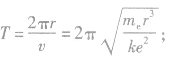
④电子在半径为r的轨道上所具有的电势能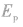
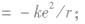
⑤等效电流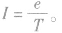 由以上各式可见,电子绕核运动的轨道半径越大,电子的运行速率越小,动能越小,电子运动的周期越大.在各轨道上具有的电视能越大。
由以上各式可见,电子绕核运动的轨道半径越大,电子的运行速率越小,动能越小,电子运动的周期越大.在各轨道上具有的电视能越大。
原子跃迁时光谱线条数的确定方法:
1.直接跃迁与间接跃迁
原子从一种能量状态跃迁到另一种能量状态时,有时可能是直接跃迁,有时可能是间接跃迁,两种情况辐射(或吸收)光子的频率可能不同。
2.一群原子和一个原子
氧原子核外只有一个电子,这个电子在某个时刻只能处在某一个可能的轨道上,在某段时间内,由某一轨道跃迁到另一个轨道时,可能的情况只有一种,但是如果容器中盛有大量的氢原子,这些原子的核外电子跃迁时就会有各种情况出现了。
3.一群氢原子处于量子数为n的激发态时,可能辐射的光谱线条数
如果氢原子处于高能级,对应量子数为n,则就有可能向量子数为(n一1),(n一2),(n一3)…1诸能级跃迁,共可形成(n一1)条谱线,而跃迁至量子数为(n一 1)的氢原子又可向(n一2),(n一3)…1诸能级跃迁,共可形成(n一2)条谱线。同理,还可以形成(n一3),(n 一4)…1条谱线。将以上分析结果归纳求和,则从量子数为n对应的能级向低能级(n—1),(n一2)…1跃迁可形成的谱线总条数为(n一1)+(n一2)+(n一3)+ …+1=n(n一1)/2。数学表示为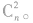
4.一个氢原子处于量子数为n的激发态时,可能辐射的光谱线条数
对于处于量子数为n的一个氢原子,它可能发生直接跃迁,只放出一个光子,也可能先跃迁到某个中间能级上,再跃迁回基态而放出两个光子,也可能逐级跃迁,即先跃迁到n一1能级上,再跃迁到n一2能级上, ……,最后回到基态上,共放出n—1个光子。即一个氢原子在发生能级跃迁时,最少放出一个光子,最多可放出n一1个光子。
利用能量守恒及氢原子能级特征解决跃迁电离等问题的方法:
在原子的跃迁及电离等过程中,总能量仍是守恒的。原子被激发时,原子的始末能级差值等于所吸收的能量,即入射光子的全部能量或者入射粒子的全部或部分能量;原子被电离时,电离能等于原子被电离前所处能级的绝对值,原子所吸收的能量等于原子电离能与电离后电离出的电子的动能之和;辐射时辐射出的光子的能量等于原子的始末能级差。氢原子的能级 F 关系为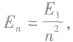 ,第n能级与量子数n2成反比,导致相邻两能级间的能量差不相等,量子数n越大,相邻能级差越小,且第n能级与第n一1能级的差比第n能级与无穷远处的能级差大,即
,第n能级与量子数n2成反比,导致相邻两能级间的能量差不相等,量子数n越大,相邻能级差越小,且第n能级与第n一1能级的差比第n能级与无穷远处的能级差大,即 另外,能级差的大小
另外,能级差的大小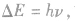 故也可利用光子能量来判定能级差大小。
故也可利用光子能量来判定能级差大小。
跃迁与电离:
激发的方式:
与“A.(选修模块3-3)(1)下列说法正确的是______A.显微镜下...”考查相似的试题有:
- 在光滑水平面上有A、B两球,其动量大小分别为10kg·m/s与15kg·m/s,方向均为向东,A球在B球后,当A球追上B球后,两球相碰,则...
- A、B两球在光滑水平面上相向运动,两球相碰后有一球停止运动,则下述说法中正确的是 ( )A.若碰后,A球速度为0,则碰前A的...
- 质量为M的小车在光滑水平面上以速度v向东行驶,一个质量为m的小球从距地面H高处自由落下,正好落入车中.此后小车的速度将( )A...
- 甲、乙两球在光滑的水平面上,沿同一直线同一方向运动,它们的动量分别为p甲=10 kg·m/s,p乙=14 kg·m/s,已知甲的速度大于...
- C、(选修模块3-5)(1)下列叙述中符合物理学史的是______A、爱因斯坦为解释光的干涉现象提出了光子说B、麦克斯韦提出了光的...
- 如图所示,一气缸竖直放置,气缸内有一质量不可忽略的活塞,将一定量的理想气体封在气缸内,活塞与气缸壁无摩擦,气体处于平...
- 一定质量的理想气体由状态A变化到状态B,压强随体积变化的关系如图,这个过程( )A.气体的密度一直变小B.气体的温度一直降...
- 在氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外发出光子,用这些光照射逸出功为2.49eV的金...
- (选修3-5)(Ⅰ)一群氢原子从 n=3 的激发态向基态跃迁时,辐射的三条谱线中,波长较长的二条谱线的波长分别为λ1和λ2,则最短...
- 下列说法正确的是( )A.当氢原子从n=2的状态跃迁到n=6的状态时,发射出光子B.放射性元素的半衰期是指大量该元素的原子核中...